真题
1 . 对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变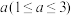 .设用
.设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是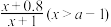 ,用
,用 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是 ,其中
,其中 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(1)分别求出方案甲以及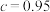 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(2)若采用方案乙,当 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
 )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变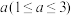 .设用
.设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是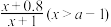 ,用
,用 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是 ,其中
,其中 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.(1)分别求出方案甲以及
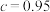 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;(2)若采用方案乙,当
 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
您最近一年使用:0次
2022-11-09更新
|
338次组卷
|
2卷引用:山东省菏泽市2023-2024学年高三上学期11月期中考试数学试题(B)
名校
解题方法
2 . 某新型双轴承电动机需要装配两个轴承才能正常工作,且两个轴承互不影响.现计划购置甲,乙两个品牌的轴承,两个品牌轴承的使用寿命及价格情况如下表:
已知甲品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.
(1)若从 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;
(2)现有两种购置方案,方案一:购置 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
品牌 | 价格(元/件) | 使用寿命(月) |
甲 |
|
|
乙 |
|
|
 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.(1)若从
 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;(2)现有两种购置方案,方案一:购置
 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
您最近一年使用:0次
2021-04-29更新
|
2676次组卷
|
6卷引用:山东省泰安市2021届高三二模数学试题
山东省泰安市2021届高三二模数学试题湖南省长沙市雅礼中学2021-2022学年高三上学期入学考试数学试题(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练山西省运城市芮城中学2021-2022学年高二下学期第一次月考数学试题人教A版(2019) 选修第三册 过关斩将 第七章 7.3.1 离散型随机变量的均值(已下线)专题13 概率综合问题-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)
解题方法
3 . 在某地区进行某种疾病调查,需要对其居民血液进行抽样化验,若结果呈阳性,则患有该疾病;若结果为阴性,则未患有该疾病.现有n(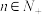 ,
, )个人,每人一份血液待检验,有如下两种方案:
)个人,每人一份血液待检验,有如下两种方案:
方案一:逐份检验,需要检验n次;
方案二:混合检验,将n份血液分别取样,混合在一起检验,若检验结果呈阴性,则n个人都未患有该疾病;若检验结果呈阳性,再对n份血液逐份检验,此时共需要检验n+1次.
(1)若 ,且其中两人患有该疾病,采用方案一,求恰好检验3次就能确定患病两人的概率;
,且其中两人患有该疾病,采用方案一,求恰好检验3次就能确定患病两人的概率;
(2)已知每个人患该疾病的概率为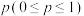 .
.
(ⅰ)若两种方案检验总次数的期望值相同,求p关于n的函数解析式 ;
;
(ⅱ)若 ,且每单次检验费用相同,为降低总检验费用,选择哪种方案更好?试说明理由.
,且每单次检验费用相同,为降低总检验费用,选择哪种方案更好?试说明理由.
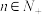 ,
, )个人,每人一份血液待检验,有如下两种方案:
)个人,每人一份血液待检验,有如下两种方案:方案一:逐份检验,需要检验n次;
方案二:混合检验,将n份血液分别取样,混合在一起检验,若检验结果呈阴性,则n个人都未患有该疾病;若检验结果呈阳性,再对n份血液逐份检验,此时共需要检验n+1次.
(1)若
 ,且其中两人患有该疾病,采用方案一,求恰好检验3次就能确定患病两人的概率;
,且其中两人患有该疾病,采用方案一,求恰好检验3次就能确定患病两人的概率;(2)已知每个人患该疾病的概率为
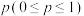 .
.(ⅰ)若两种方案检验总次数的期望值相同,求p关于n的函数解析式
 ;
;(ⅱ)若
 ,且每单次检验费用相同,为降低总检验费用,选择哪种方案更好?试说明理由.
,且每单次检验费用相同,为降低总检验费用,选择哪种方案更好?试说明理由.
您最近一年使用:0次
名校
4 . “东方味王”餐饮公司入驻某校,为满足学生餐饮需求、丰富菜品花色,研发了一套新产品.该产品每份成本6元,售价8元,产品保质期为两天,若两天内未售出,则产品过期报废.公司为决策每两天的产量,先进行试销,统计并整理连续30天的日销量(单位:百份),假设该新产品每日销量相互独立,得到如下的柱状图:

(1)以试销统计的频率为概率,记每两天中销售该新产品的总份数为 (单位:百份),求
(单位:百份),求 的分布列和数学期望;
的分布列和数学期望;
(2)以该新产品两天内获得利润较大为决策依据,在每两天生产配送27百份,28百份两种方案中应选择哪种?

(1)以试销统计的频率为概率,记每两天中销售该新产品的总份数为
 (单位:百份),求
(单位:百份),求 的分布列和数学期望;
的分布列和数学期望;(2)以该新产品两天内获得利润较大为决策依据,在每两天生产配送27百份,28百份两种方案中应选择哪种?
您最近一年使用:0次
2022-07-16更新
|
801次组卷
|
5卷引用:山东省烟台市招远市招远第一中学2022-2023学年高二下学期期中数学试题
山东省烟台市招远市招远第一中学2022-2023学年高二下学期期中数学试题福建省福州市八县(市)协作校2021-2022学年高二下学期期末联考数学试题(已下线)第四章 概率与统计(A卷·知识通关练)(3)福建省连城县第一中学2022-2023学年高二下学期5月月考数学试题(已下线)考点18 决策的选择问题 2024届高考数学考点总动员
名校
解题方法
5 . 某医疗机构,为了研究某种病毒在人群中的传播特征,需要检测血液是否为阳性.若现有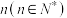 份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
方式一:逐份检测,需检测 次;
次;
方式二:混合检测,将其中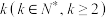 份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这
份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这 份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这
份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这 份样本逐份检测,因此检测总次数为
份样本逐份检测,因此检测总次数为 次,假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是
次,假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是 .
.
(1)在某地区,通过随机检测发现该地区人群血液为阳性的概率约为0.8%.为了调查某单位该病毒感染情况,随机选取50人进行检测,有两个分组方案:
方案一:将50人分成10组,每组5人;
方案二:将50人分成5组,每组10人.
试分析哪种方案的检测总次数更少?
(取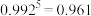 ,
,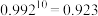 ,
, )
)
(2)现取其中 份血液样本,若采用逐份检验方式,需要检测的总次数为
份血液样本,若采用逐份检验方式,需要检测的总次数为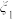 ;采用混合检测方式,需要检测的总次数为
;采用混合检测方式,需要检测的总次数为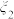 .若
.若 ,试解决以下问题:
,试解决以下问题:
①确定 关于
关于 的函数关系;
的函数关系;
②当 为何值时,
为何值时, 取最大值并求出最大值.
取最大值并求出最大值.
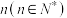 份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:
份血液样本,每份样本被取到的可能性相同,检测方式有以下两种:方式一:逐份检测,需检测
 次;
次;方式二:混合检测,将其中
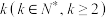 份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这
份血液样本分别取样混合在一起检测,若检测结果为阴性,说明这 份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这
份样本全为阴性,则只需检测1次;若检测结果为阳性,则需要对这 份样本逐份检测,因此检测总次数为
份样本逐份检测,因此检测总次数为 次,假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是
次,假设每份样本被检测为阳性或阴性是相互独立的,且每份样本为阳性的概率是 .
.(1)在某地区,通过随机检测发现该地区人群血液为阳性的概率约为0.8%.为了调查某单位该病毒感染情况,随机选取50人进行检测,有两个分组方案:
方案一:将50人分成10组,每组5人;
方案二:将50人分成5组,每组10人.
试分析哪种方案的检测总次数更少?
(取
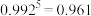 ,
,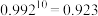 ,
, )
)(2)现取其中
 份血液样本,若采用逐份检验方式,需要检测的总次数为
份血液样本,若采用逐份检验方式,需要检测的总次数为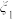 ;采用混合检测方式,需要检测的总次数为
;采用混合检测方式,需要检测的总次数为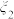 .若
.若 ,试解决以下问题:
,试解决以下问题:①确定
 关于
关于 的函数关系;
的函数关系;②当
 为何值时,
为何值时, 取最大值并求出最大值.
取最大值并求出最大值.
您最近一年使用:0次
2020-07-25更新
|
1069次组卷
|
6卷引用:山东省枣庄市市中区第三中学2022-2023学年高二下学期5月月考数学试题
名校
解题方法
6 . 给出下列命题,其中正确的命题有( )
A.若 .则 .则 |
B.公共汽车上有10位乘客,沿途5个车站,乘客下车的可能方式有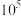 种 种 |
| C.从6双不同颜色的鞋子中任取4只,其中恰好只有一双同色的取法有240种 |
D.西部某县委将7位大学生志愿者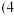 男3女)分成两组,分配到两所小学支教,若要求女生不能单独成组,且每组最多5人,则不同的分配方案共有104种 男3女)分成两组,分配到两所小学支教,若要求女生不能单独成组,且每组最多5人,则不同的分配方案共有104种 |
您最近一年使用:0次
昨日更新
|
392次组卷
|
2卷引用:山东省泰安市新泰市第一中学东校2023-2024学年高二下学期第二次质量检测数学试题
7 . 某学校数学实践小组为该校一块长方形空地设计种树方案,在坐标纸上设计如下:第 棵树种在点
棵树种在点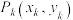 处,其中
处,其中 ,当
,当 时,
时,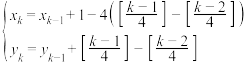 ,[
,[ ]表示不大于x的最大整数,按此设计方案,第3株树种植点的坐标为
]表示不大于x的最大整数,按此设计方案,第3株树种植点的坐标为___________ ;第2025棵树种植点的坐标为____________ .
 棵树种在点
棵树种在点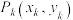 处,其中
处,其中 ,当
,当 时,
时,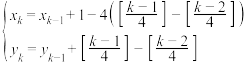 ,[
,[ ]表示不大于x的最大整数,按此设计方案,第3株树种植点的坐标为
]表示不大于x的最大整数,按此设计方案,第3株树种植点的坐标为
您最近一年使用:0次
2024-05-11更新
|
216次组卷
|
2卷引用:山东省潍坊市2023-2024学年高二下学期期中质量监测数学试题
8 . 已知 的内角
的内角 所对边分别为
所对边分别为 .若
.若 内部有一个圆心为
内部有一个圆心为 ,半径为
,半径为 米的圆,它沿着
米的圆,它沿着 的边内侧滚动一周,且始终保持与三角形的至少一条边相切.
的边内侧滚动一周,且始终保持与三角形的至少一条边相切. 为边长是16米的等边三角形,求圆心
为边长是16米的等边三角形,求圆心 经过的路程;
经过的路程;
(2)若用28米的材料刚好围成这个三角形,请你设计一种 的围成方案,使得圆心
的围成方案,使得圆心 经过的路程最大并求出该最大值(若
经过的路程最大并求出该最大值(若 为正数,则
为正数,则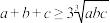 ,当且仅当
,当且仅当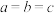 时取等号).
时取等号).
 的内角
的内角 所对边分别为
所对边分别为 .若
.若 内部有一个圆心为
内部有一个圆心为 ,半径为
,半径为 米的圆,它沿着
米的圆,它沿着 的边内侧滚动一周,且始终保持与三角形的至少一条边相切.
的边内侧滚动一周,且始终保持与三角形的至少一条边相切.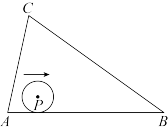
 为边长是16米的等边三角形,求圆心
为边长是16米的等边三角形,求圆心 经过的路程;
经过的路程;(2)若用28米的材料刚好围成这个三角形,请你设计一种
 的围成方案,使得圆心
的围成方案,使得圆心 经过的路程最大并求出该最大值(若
经过的路程最大并求出该最大值(若 为正数,则
为正数,则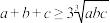 ,当且仅当
,当且仅当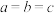 时取等号).
时取等号).
您最近一年使用:0次
2023-07-14更新
|
414次组卷
|
2卷引用:山东省潍坊市2022-2023学年高一下学期期末数学试题
名校
解题方法
9 . 某精密仪器生产厂家计划对本厂工人进行技能考核,方案如下:每名工人连续生产出10件产品,若经检验后有不低于9件的合格产品,则将该工人技能考核评为合格等次,考核结束;否则,将不合格产品交回该工人,调试后经再次检验,若全部合格,则将该工人技能考核评为合格,考核结束,否则,将该工人技能考核评为不合格,需脱产进行培训.设工人甲生产或调试每件产品合格的概率均为 ,且生产或调试每件产品是否合格互不影响.
,且生产或调试每件产品是否合格互不影响.
(1)求工人甲只生产10件产品即结束考核的概率;
(2)若X表示工人甲生产和调试的产品件数之和,求随机变量X的数学期望 .
.
 ,且生产或调试每件产品是否合格互不影响.
,且生产或调试每件产品是否合格互不影响.(1)求工人甲只生产10件产品即结束考核的概率;
(2)若X表示工人甲生产和调试的产品件数之和,求随机变量X的数学期望
 .
.
您最近一年使用:0次
2023-04-27更新
|
1262次组卷
|
4卷引用:山东省烟台市2022-2023学年高二下学期期中数学试题
山东省烟台市2022-2023学年高二下学期期中数学试题辽宁省沈阳市东北育才学校2022-2023学年高二下学期期中数学试题(已下线)第8章:概率 重点题型复习-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)(已下线)专题02 高二下期末真题精选(压轴题 )-高二期末考点大串讲(人教A版2019)
名校
解题方法
10 . 6名研究人员在3个无菌研究舱同时进行工作,由于空间限制,每个舱至少1人,至多3人,则不同的安排方案共有( )
| A.360种 | B.180种 | C.720种 | D.450种 |
您最近一年使用:0次
2023-04-07更新
|
2042次组卷
|
6卷引用:山东省青岛市青岛第十七中学2022-2023学年高二下学期期中数学试题





