1 . 已知无穷数列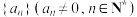 ,构造新数列
,构造新数列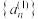 满足
满足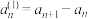 ,
,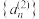 满足
满足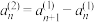 ,
, ,
,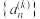 满足
满足 ,若
,若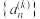 为常数数列,则称
为常数数列,则称 为
为 阶等差数列;同理令
阶等差数列;同理令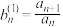 ,
,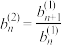 ,
, ,
,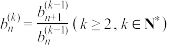 ,若
,若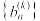 为常数数列,则称
为常数数列,则称 为
为 阶等比数列.
阶等比数列.
(1)已知 为二阶等差数列,且
为二阶等差数列,且 ,
, ,
,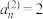 ,求
,求 的通项公式;
的通项公式;
(2)若 为
为 阶等差数列,
阶等差数列, 为一阶等比数列,证明:
为一阶等比数列,证明: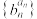 为
为 阶等比数列;
阶等比数列;
(3)已知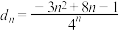 ,令
,令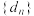 的前
的前 项和为
项和为 ,
,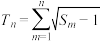 ,证明:
,证明: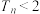 .
.
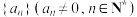 ,构造新数列
,构造新数列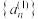 满足
满足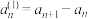 ,
,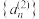 满足
满足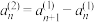 ,
, ,
,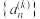 满足
满足 ,若
,若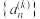 为常数数列,则称
为常数数列,则称 为
为 阶等差数列;同理令
阶等差数列;同理令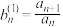 ,
,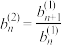 ,
, ,
,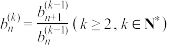 ,若
,若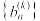 为常数数列,则称
为常数数列,则称 为
为 阶等比数列.
阶等比数列.(1)已知
 为二阶等差数列,且
为二阶等差数列,且 ,
, ,
,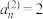 ,求
,求 的通项公式;
的通项公式;(2)若
 为
为 阶等差数列,
阶等差数列, 为一阶等比数列,证明:
为一阶等比数列,证明: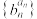 为
为 阶等比数列;
阶等比数列;(3)已知
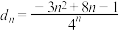 ,令
,令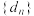 的前
的前 项和为
项和为 ,
,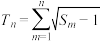 ,证明:
,证明: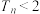 .
.
您最近一年使用:0次
2024高三上·全国·专题练习
解题方法
2 . 如图 ,已知椭圆
,已知椭圆 的方程为
的方程为 和椭圆
和椭圆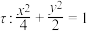 ,其中
,其中 分别是椭圆
分别是椭圆 的左右顶点.
的左右顶点. 恰好为椭圆
恰好为椭圆 的两个焦点,椭圆
的两个焦点,椭圆 和椭圆
和椭圆 有相同的离心率,求椭圆
有相同的离心率,求椭圆 的方程;
的方程;
(2)如图 ,若椭圆
,若椭圆 的方程为
的方程为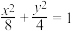 .
. 是椭圆
是椭圆 上一点,射线
上一点,射线 分别交椭圆
分别交椭圆 于
于 ,连接
,连接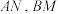 (
(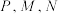 均在
均在 轴上方).求证:
轴上方).求证: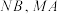 斜率之积
斜率之积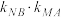 为定值,求出这个定值;
为定值,求出这个定值;
(3)在(2)的条件下,若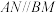 ,且两条平行线的斜率为
,且两条平行线的斜率为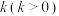 ,求正数
,求正数 的值.
的值.
 ,已知椭圆
,已知椭圆 的方程为
的方程为 和椭圆
和椭圆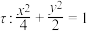 ,其中
,其中 分别是椭圆
分别是椭圆 的左右顶点.
的左右顶点.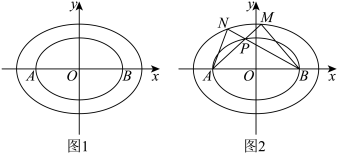
 恰好为椭圆
恰好为椭圆 的两个焦点,椭圆
的两个焦点,椭圆 和椭圆
和椭圆 有相同的离心率,求椭圆
有相同的离心率,求椭圆 的方程;
的方程;(2)如图
 ,若椭圆
,若椭圆 的方程为
的方程为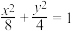 .
. 是椭圆
是椭圆 上一点,射线
上一点,射线 分别交椭圆
分别交椭圆 于
于 ,连接
,连接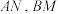 (
(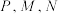 均在
均在 轴上方).求证:
轴上方).求证: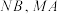 斜率之积
斜率之积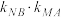 为定值,求出这个定值;
为定值,求出这个定值;(3)在(2)的条件下,若
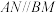 ,且两条平行线的斜率为
,且两条平行线的斜率为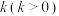 ,求正数
,求正数 的值.
的值.
您最近一年使用:0次
3 . 某纺织厂4月份生产了三种类型的纱线,分别为大卷纱线、中卷纱线和小卷纱线,其中大卷纱线有2000卷,中卷纱线有8000卷,小卷纱线有20000卷.为检查该纺织厂4月份生产的这三种类型纱线的质量,按比例用分层随机抽样的方法从中抽检240卷,则被抽检的小卷纱线有( )
| A.120卷 | B.150卷 | C.160卷 | D.200卷 |
您最近一年使用:0次
2024·全国·模拟预测
4 . 甲、乙两名小朋友,每人手中各有3张龙年纪念卡片,其中甲手中的3张卡片为1张金色和2张银色,乙手中的3张卡片都是金色的,现在两人各从自己的卡片中随机取1张,去与对方交换,重复 次这样的操作,记甲手中银色纪念卡片
次这样的操作,记甲手中银色纪念卡片 张,恰有2张银色纪念卡片的概率为
张,恰有2张银色纪念卡片的概率为 ,恰有1张银色纪念卡片的概率为
,恰有1张银色纪念卡片的概率为 .
.
(1)求 的值.
的值.
(2)问操作几次甲手中银色纪念卡片就可能首次出现0张,求首次出现这种情况的概率 .
.
(3)记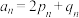 .
.
(i)证明数列 为等比数列,并求出
为等比数列,并求出 的通项公式.
的通项公式.
(ii)求 的分布列及数学期望.(用
的分布列及数学期望.(用 表示)
表示)
 次这样的操作,记甲手中银色纪念卡片
次这样的操作,记甲手中银色纪念卡片 张,恰有2张银色纪念卡片的概率为
张,恰有2张银色纪念卡片的概率为 ,恰有1张银色纪念卡片的概率为
,恰有1张银色纪念卡片的概率为 .
.(1)求
 的值.
的值.(2)问操作几次甲手中银色纪念卡片就可能首次出现0张,求首次出现这种情况的概率
 .
.(3)记
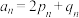 .
.(i)证明数列
 为等比数列,并求出
为等比数列,并求出 的通项公式.
的通项公式.(ii)求
 的分布列及数学期望.(用
的分布列及数学期望.(用 表示)
表示)
您最近一年使用:0次
名校
解题方法
5 . 实验 :甲、乙、丙三名同学各自从
:甲、乙、丙三名同学各自从 、
、 、
、 中选了一个字母(不可重复).记事件
中选了一个字母(不可重复).记事件 为“乙同学选字母
为“乙同学选字母 ”,事件
”,事件 为“甲同学没有选字母
为“甲同学没有选字母 ”,则下列正确的有( )
”,则下列正确的有( )
 :甲、乙、丙三名同学各自从
:甲、乙、丙三名同学各自从 、
、 、
、 中选了一个字母(不可重复).记事件
中选了一个字母(不可重复).记事件 为“乙同学选字母
为“乙同学选字母 ”,事件
”,事件 为“甲同学没有选字母
为“甲同学没有选字母 ”,则下列正确的有( )
”,则下列正确的有( )A.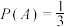 | B.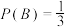 |
C. | D.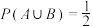 |
您最近一年使用:0次
7日内更新
|
523次组卷
|
4卷引用:核心考点10 概率 A基础卷 (高一期末考试必考的10大核心考点)
(已下线)核心考点10 概率 A基础卷 (高一期末考试必考的10大核心考点) (已下线)专题15.1概率-重难点突破及混淆易错规避(苏教版2019必修第二册)甘肃省庆阳市环县第一中学2023-2024学年高二上学期期末考试数学试题西藏山南市第二高级中学2023-2024学年高二上学期期末考试数学试题
解题方法
6 . 有以下6个函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤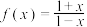 ;⑥
;⑥ .记事件
.记事件 :从中任取1个函数是奇函数;事件
:从中任取1个函数是奇函数;事件 :从中任取1个函数是偶函数,事件
:从中任取1个函数是偶函数,事件 的对立事件分别为
的对立事件分别为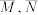 ,则( )
,则( )
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤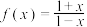 ;⑥
;⑥ .记事件
.记事件 :从中任取1个函数是奇函数;事件
:从中任取1个函数是奇函数;事件 :从中任取1个函数是偶函数,事件
:从中任取1个函数是偶函数,事件 的对立事件分别为
的对立事件分别为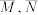 ,则( )
,则( )A. |
B.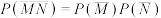 |
C.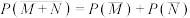 |
D. |
您最近一年使用:0次
7日内更新
|
289次组卷
|
4卷引用:概率、随机变量及其分布-综合测试卷B卷
(已下线)概率、随机变量及其分布-综合测试卷B卷2024届河南省名校联盟考前模拟大联考三模数学试题河南省濮阳市2024届高三第三次模拟考试数学试题海南省2020-2021学年高二下学期期末考试数学试题
名校
7 . 在等腰梯形 中,CD的中点为O,以O为坐标原点,DC所在直线为x轴,建立如图所示的平面直角坐标系,已知
中,CD的中点为O,以O为坐标原点,DC所在直线为x轴,建立如图所示的平面直角坐标系,已知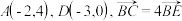 .
.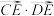 ;
;
(2)若点F在线段CD上, ,求
,求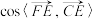 .
.
 中,CD的中点为O,以O为坐标原点,DC所在直线为x轴,建立如图所示的平面直角坐标系,已知
中,CD的中点为O,以O为坐标原点,DC所在直线为x轴,建立如图所示的平面直角坐标系,已知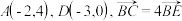 .
.
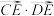 ;
;(2)若点F在线段CD上,
 ,求
,求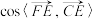 .
.
您最近一年使用:0次
7日内更新
|
275次组卷
|
4卷引用:平面向量-综合测试卷B卷
8 . 已知函数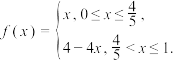 随机变量
随机变量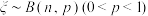 ,随机变量
,随机变量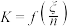 ,
, 的期望为
的期望为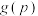 .
.
(1)当 时,求
时,求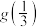 ;
;
(2)当 时,求
时,求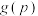 的表达式.
的表达式.
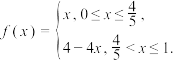 随机变量
随机变量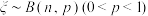 ,随机变量
,随机变量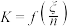 ,
, 的期望为
的期望为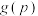 .
.(1)当
 时,求
时,求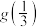 ;
;(2)当
 时,求
时,求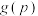 的表达式.
的表达式.
您最近一年使用:0次
7日内更新
|
257次组卷
|
4卷引用:概率、随机变量及其分布-综合测试卷B卷
(已下线)概率、随机变量及其分布-综合测试卷B卷河南省部分重点高中2023-2024学年高三下学期5月联考数学试卷 (新高考)(已下线)辽宁省沈阳市第二中学2024届高三下学期三模数学试题内蒙古自治区锡林郭勒盟2024届高三下学期5月模拟考试理科数学试题
名校
解题方法
9 . 多年统计数据表明如果甲、乙两位选手在决赛中相遇,甲每局比赛获胜的概率为 ,乙每局比赛获胜的概率为
,乙每局比赛获胜的概率为 .本次世界大赛,这两位选手又在决赛中相遇.赛制为五局三胜制(最先获得三局胜利者获得冠军).
.本次世界大赛,这两位选手又在决赛中相遇.赛制为五局三胜制(最先获得三局胜利者获得冠军).
(1)现在比赛正在进行,而且乙暂时以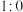 领先,求甲最终获得冠军的概率;
领先,求甲最终获得冠军的概率;
(2)若本次决赛最终甲以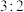 的大比分获得冠军,求甲失分局序号之和
的大比分获得冠军,求甲失分局序号之和 的分布列和数学期望.
的分布列和数学期望.
 ,乙每局比赛获胜的概率为
,乙每局比赛获胜的概率为 .本次世界大赛,这两位选手又在决赛中相遇.赛制为五局三胜制(最先获得三局胜利者获得冠军).
.本次世界大赛,这两位选手又在决赛中相遇.赛制为五局三胜制(最先获得三局胜利者获得冠军).(1)现在比赛正在进行,而且乙暂时以
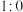 领先,求甲最终获得冠军的概率;
领先,求甲最终获得冠军的概率;(2)若本次决赛最终甲以
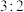 的大比分获得冠军,求甲失分局序号之和
的大比分获得冠军,求甲失分局序号之和 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
7日内更新
|
402次组卷
|
4卷引用:概率、随机变量及其分布-综合测试卷A卷
(已下线)概率、随机变量及其分布-综合测试卷A卷2024届河南省名校联盟考前模拟大联考三模数学试题陕西省西安市第一中学2023-2024学年高三下学期高考考前模拟考试理科数学试题河南省濮阳市2024届高三第三次模拟考试数学试题
名校
10 . 对于平面向量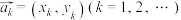 ,定义“
,定义“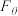 变换”:
变换”: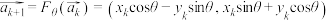 ,
,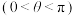
(1)若向量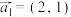 ,
,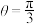 ,求
,求 ;
;
(2)已知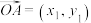 ,
,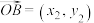 ,且
,且 与
与 不平行,
不平行,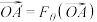 ,
,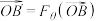 ,证明:
,证明: .
.
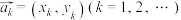 ,定义“
,定义“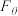 变换”:
变换”: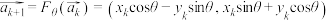 ,
,
(1)若向量
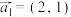 ,
,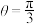 ,求
,求 ;
;(2)已知
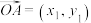 ,
,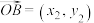 ,且
,且 与
与 不平行,
不平行,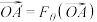 ,
,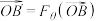 ,证明:
,证明: .
.
您最近一年使用:0次



