23-24高二上·上海·课后作业
1 . 请指出下列各题用数学归纳法证明过程中的错误.
(1)设 为正整数,求证:
为正整数,求证: .
.
证明:假设当 (
( 为正整数)时等式成立,即有
为正整数)时等式成立,即有 .
.
那么当 时,就有
时,就有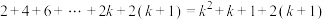
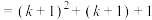 .因此,对于任何正整数
.因此,对于任何正整数 等式都成立.
等式都成立.
(2)设 为正整数,求证:
为正整数,求证: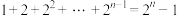 .
.
证明:①当 时,左边
时,左边 ,右边
,右边 ,等式成立.
,等式成立.
②假设当 (
(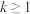 ,
, 为正整数)时,等式成立,即有
为正整数)时,等式成立,即有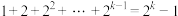 ,
,
那么当 时,由等比数列求和公式,就有
时,由等比数列求和公式,就有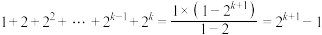 ,等式也成立.
,等式也成立.
根据(1)和(2),由数学归纳法可以断定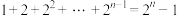 对任何正整数
对任何正整数 都成立.
都成立.
(1)设
 为正整数,求证:
为正整数,求证: .
.证明:假设当
 (
( 为正整数)时等式成立,即有
为正整数)时等式成立,即有 .
.那么当
 时,就有
时,就有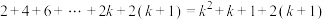
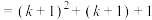 .因此,对于任何正整数
.因此,对于任何正整数 等式都成立.
等式都成立.(2)设
 为正整数,求证:
为正整数,求证: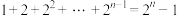 .
.证明:①当
 时,左边
时,左边 ,右边
,右边 ,等式成立.
,等式成立.②假设当
 (
(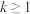 ,
, 为正整数)时,等式成立,即有
为正整数)时,等式成立,即有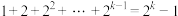 ,
,那么当
 时,由等比数列求和公式,就有
时,由等比数列求和公式,就有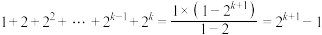 ,等式也成立.
,等式也成立.根据(1)和(2),由数学归纳法可以断定
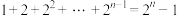 对任何正整数
对任何正整数 都成立.
都成立.
您最近一年使用:0次
2 . 已知函数 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足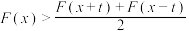 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.
(1)试判断函数 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);
(2)若函数 具有“性质
具有“性质 ”,且
”,且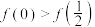 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;
(3)若函数 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,
①若 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;
②若 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
 的定义域为
的定义域为 ,
, 为大于
为大于 的常数,对任意
的常数,对任意 ,都满足
,都满足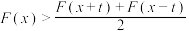 ,则称函数
,则称函数 在
在 上具有“性质
上具有“性质 ”.
”.(1)试判断函数
 和函数
和函数 是否具有“性质
是否具有“性质 ”(无需证明);
”(无需证明);(2)若函数
 具有“性质
具有“性质 ”,且
”,且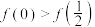 ,求证:对任意
,求证:对任意 ,都有
,都有 ;
;(3)若函数
 的定义域为
的定义域为 ,且具有“性质
,且具有“性质 ”,试判断下列命题的真假,并说明理由,
”,试判断下列命题的真假,并说明理由,①若
 在区间
在区间 上是严格增函数,则此函数在
上是严格增函数,则此函数在 上也是严格增函数;
上也是严格增函数;②若
 在区间
在区间 上是严格减函数,则此函数在
上是严格减函数,则此函数在 上也是严格减函数.
上也是严格减函数.
您最近一年使用:0次
2023-01-12更新
|
630次组卷
|
6卷引用:上海市闵行区2022-2023学年高一上学期期末数学试题
上海市闵行区2022-2023学年高一上学期期末数学试题(已下线)专题10 指数及指数函数压轴题-【常考压轴题】(已下线)第五章 函数的概念、性质及应用(压轴必刷30题9种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(10个考点专练)-【满分全攻略】(沪教版2020必修第一册)(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】(人教A版2019必修第一册)(已下线)第四章 指数函数与对数函数-【优化数学】单元测试能力卷(人教A版2019)
名校
解题方法
3 . 已知函数 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间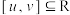 ,存在
,存在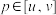 且
且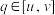 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.
(1)求证: 是
是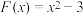 的生成函数;
的生成函数;
(2)若 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;
(3)若 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间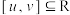 ,存在
,存在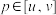 且
且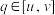 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.(1)求证:
 是
是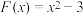 的生成函数;
的生成函数;(2)若
 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;(3)若
 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
您最近一年使用:0次
2023-05-05更新
|
572次组卷
|
4卷引用:上海交通大学附属中学2022-2023学年高一下学期期中数学试题
上海交通大学附属中学2022-2023学年高一下学期期中数学试题湖南省长沙市明德中学2022-2023学年高一下学期5月月考数学试题(已下线)第3课时 课后 函数的单调性(完成)(已下线)5.2.2 函数的单调性-数学同步精品课堂(沪教版2020必修第一册)
解题方法
4 . 已知抛物线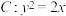 ,
,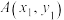 ,
,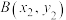 是C上两个不同的点.
是C上两个不同的点.
(1)求证:直线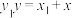 与C相切;
与C相切;
(2)若O为坐标原点,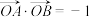 ,C在A,B处的切线交于点P,证明:点P在定直线上.
,C在A,B处的切线交于点P,证明:点P在定直线上.
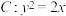 ,
,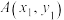 ,
,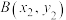 是C上两个不同的点.
是C上两个不同的点.(1)求证:直线
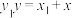 与C相切;
与C相切;(2)若O为坐标原点,
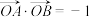 ,C在A,B处的切线交于点P,证明:点P在定直线上.
,C在A,B处的切线交于点P,证明:点P在定直线上.
您最近一年使用:0次
2022-07-25更新
|
1236次组卷
|
6卷引用:江西省名校联考2023届高三7月第一次摸底测试数学(理)试题
江西省名校联考2023届高三7月第一次摸底测试数学(理)试题抛物线的综合问题(已下线)专题6 判断位置关系的运算(基础版)(已下线)专题3.14 直线与抛物线的位置关系-重难点题型检测-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)专题3-6 抛物线综合大题归类(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)(已下线)专题05 抛物线8种常见考法归类(2)
解题方法
5 . 我们用 ,
, ,
, ,…,
,…, (
( ,且
,且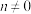 )表示n个变量,就如同a、b、c、d、e、f等表示变量一样.已知
)表示n个变量,就如同a、b、c、d、e、f等表示变量一样.已知 ,
, ,
, ,…,
,…, (
( ,且
,且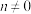 )均为正数.
)均为正数.
(1)求证: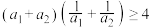 ;
;
(2)求证: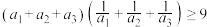 ;
;
(3)请将命题(1)、(2)推广到一般情形(不作证明).
 ,
, ,
, ,…,
,…, (
( ,且
,且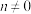 )表示n个变量,就如同a、b、c、d、e、f等表示变量一样.已知
)表示n个变量,就如同a、b、c、d、e、f等表示变量一样.已知 ,
, ,
, ,…,
,…, (
( ,且
,且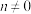 )均为正数.
)均为正数.(1)求证:
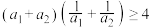 ;
;(2)求证:
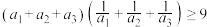 ;
;(3)请将命题(1)、(2)推广到一般情形(不作证明).
您最近一年使用:0次
解题方法
6 . (1)叙述并证明直线与平面平行的性质定理(要求写出已知、求证、证明过程并画图);
(2)叙述并证明三垂线定理(要求写出已知、求证、证明过程并画图);
(3)叙述并证明两个平面平行的判定定理(要求写出已知、求证、证明过程并画图).
(2)叙述并证明三垂线定理(要求写出已知、求证、证明过程并画图);
(3)叙述并证明两个平面平行的判定定理(要求写出已知、求证、证明过程并画图).
您最近一年使用:0次
名校
解题方法
7 . 假设视网膜为一个平面,光在空气中不折射,眼球的成像原理为小孔成像. 思考如下成像原理: 如图,地面内有圆 ,其圆心在线段
,其圆心在线段 上,且与线段
上,且与线段 交于不与
交于不与 重合的点
重合的点 ,
, 地面,且
地面,且 ,
, 点为人眼所在处,视网膜平面与直线
点为人眼所在处,视网膜平面与直线 垂直. 过
垂直. 过 点作平面
点作平面 平行于视网膜平面. 科学家已经证明,这种情况下圆
平行于视网膜平面. 科学家已经证明,这种情况下圆 上任意一点到
上任意一点到 点的直线与平面
点的直线与平面 交点的轨迹(令为曲线
交点的轨迹(令为曲线 )为椭圆或圆,且由于小孔成像,曲线
)为椭圆或圆,且由于小孔成像,曲线 与圆
与圆 在视网膜平面上的影像是相似的,则当视网膜平面上的圆
在视网膜平面上的影像是相似的,则当视网膜平面上的圆 的影像为圆时,圆
的影像为圆时,圆 的半径
的半径 为
为____________ . 当圆 的半径
的半径 满足
满足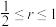 时,视网膜平面上的圆
时,视网膜平面上的圆 的影像的离心率的取值范围为
的影像的离心率的取值范围为____________ .
 ,其圆心在线段
,其圆心在线段 上,且与线段
上,且与线段 交于不与
交于不与 重合的点
重合的点 ,
, 地面,且
地面,且 ,
, 点为人眼所在处,视网膜平面与直线
点为人眼所在处,视网膜平面与直线 垂直. 过
垂直. 过 点作平面
点作平面 平行于视网膜平面. 科学家已经证明,这种情况下圆
平行于视网膜平面. 科学家已经证明,这种情况下圆 上任意一点到
上任意一点到 点的直线与平面
点的直线与平面 交点的轨迹(令为曲线
交点的轨迹(令为曲线 )为椭圆或圆,且由于小孔成像,曲线
)为椭圆或圆,且由于小孔成像,曲线 与圆
与圆 在视网膜平面上的影像是相似的,则当视网膜平面上的圆
在视网膜平面上的影像是相似的,则当视网膜平面上的圆 的影像为圆时,圆
的影像为圆时,圆 的半径
的半径 为
为 的半径
的半径 满足
满足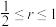 时,视网膜平面上的圆
时,视网膜平面上的圆 的影像的离心率的取值范围为
的影像的离心率的取值范围为
您最近一年使用:0次
2024-05-09更新
|
103次组卷
|
2卷引用:四川省成都市实验外国语学校2023-2024学年高二上学期期末能力测评数学试题
名校
8 . 函数的凹凸性的定义是由丹麦著名的数学家兼工程师Johan Jensen在1905年提出来的.其中对于凸函数的定义如下:设连续函数 的定义域为
的定义域为 (或开区间
(或开区间 或
或 ,或
,或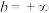 都可以),若对于区间
都可以),若对于区间 上任意两个数
上任意两个数 ,均有
,均有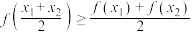 成立,则称
成立,则称 为区间
为区间 上的凸函数.容易证明譬如
上的凸函数.容易证明譬如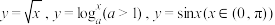 都是凸函数.Johan Jensen在1906年将上述不等式推广到了
都是凸函数.Johan Jensen在1906年将上述不等式推广到了 个变量的情形,即著名的Jensen不等式:若函数
个变量的情形,即著名的Jensen不等式:若函数 为其定义域上的凸函数,则对其定义域内任意
为其定义域上的凸函数,则对其定义域内任意 个数
个数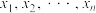 ,均有
,均有 成立,当且仅当
成立,当且仅当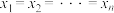 时等号成立.
时等号成立.
(1)若函数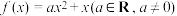 为
为 上的凸函数,求
上的凸函数,求 的取值范围:
的取值范围:
(2)在 中,求
中,求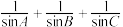 的最小值;
的最小值;
(3)若连续函数 的定义域和值域都是
的定义域和值域都是 ,且对于任意
,且对于任意 均满足下述两个不等式:
均满足下述两个不等式: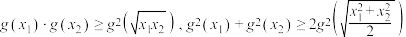 ,证明:函数
,证明:函数 为
为 上的凸函数.(注:
上的凸函数.(注: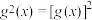 )
)
 的定义域为
的定义域为 (或开区间
(或开区间 或
或 ,或
,或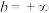 都可以),若对于区间
都可以),若对于区间 上任意两个数
上任意两个数 ,均有
,均有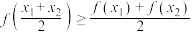 成立,则称
成立,则称 为区间
为区间 上的凸函数.容易证明譬如
上的凸函数.容易证明譬如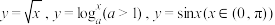 都是凸函数.Johan Jensen在1906年将上述不等式推广到了
都是凸函数.Johan Jensen在1906年将上述不等式推广到了 个变量的情形,即著名的Jensen不等式:若函数
个变量的情形,即著名的Jensen不等式:若函数 为其定义域上的凸函数,则对其定义域内任意
为其定义域上的凸函数,则对其定义域内任意 个数
个数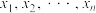 ,均有
,均有 成立,当且仅当
成立,当且仅当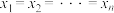 时等号成立.
时等号成立.(1)若函数
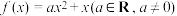 为
为 上的凸函数,求
上的凸函数,求 的取值范围:
的取值范围:(2)在
 中,求
中,求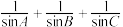 的最小值;
的最小值;(3)若连续函数
 的定义域和值域都是
的定义域和值域都是 ,且对于任意
,且对于任意 均满足下述两个不等式:
均满足下述两个不等式: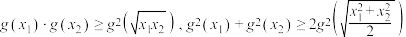 ,证明:函数
,证明:函数 为
为 上的凸函数.(注:
上的凸函数.(注: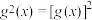 )
)
您最近一年使用:0次
解题方法
9 . 离散对数在密码学中有重要的应用.设 是素数,集合
是素数,集合 ,若
,若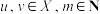 ,记
,记 为
为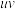 除以
除以 的余数,
的余数,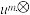 为
为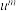 除以
除以 的余数;设
的余数;设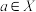 ,
, 两两不同,若
两两不同,若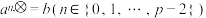 ,则称
,则称 是以
是以 为底
为底 的离散对数,记为
的离散对数,记为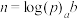 .
.
(1)若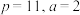 ,求
,求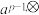 ;
;
(2)对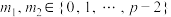 ,记
,记 为
为 除以
除以 的余数(当
的余数(当 能被
能被 整除时,
整除时, ).证明:
).证明: ,其中
,其中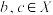 ;
;
(3)已知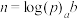 .对
.对 ,令
,令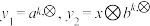 .证明:
.证明: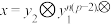 .
.
 是素数,集合
是素数,集合 ,若
,若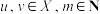 ,记
,记 为
为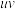 除以
除以 的余数,
的余数,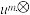 为
为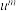 除以
除以 的余数;设
的余数;设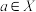 ,
, 两两不同,若
两两不同,若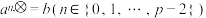 ,则称
,则称 是以
是以 为底
为底 的离散对数,记为
的离散对数,记为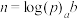 .
.(1)若
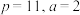 ,求
,求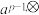 ;
;(2)对
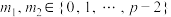 ,记
,记 为
为 除以
除以 的余数(当
的余数(当 能被
能被 整除时,
整除时, ).证明:
).证明: ,其中
,其中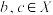 ;
;(3)已知
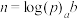 .对
.对 ,令
,令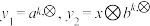 .证明:
.证明: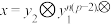 .
.
您最近一年使用:0次
2024-01-19更新
|
6538次组卷
|
8卷引用:2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题
2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题(已下线)2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题变式题16-192024年九省联考试卷分析及真题鉴赏(已下线)压轴题高等数学背景下新定义题(九省联考第19题模式)讲(已下线)微考点8-1 新高考新题型19题新定义题型精选(已下线)新题型02 新高考新结构竞赛题型十五大考点汇总-2(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)专题8 考前押题大猜想36-40
名校
解题方法
10 . 已知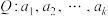 为有穷正整数数列,且
为有穷正整数数列,且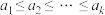 ,集合
,集合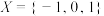 .若存在
.若存在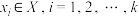 ,使得
,使得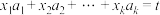 ,则称
,则称 为
为 可表数,称集合
可表数,称集合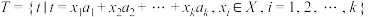 为
为 可表集.
可表集.
(1)若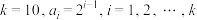 ,判定31,1024是否为
,判定31,1024是否为 可表数,并说明理由;
可表数,并说明理由;
(2)若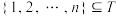 ,证明:
,证明: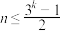 ;
;
(3)设 ,若
,若 ,求
,求 的最小值.
的最小值.
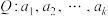 为有穷正整数数列,且
为有穷正整数数列,且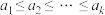 ,集合
,集合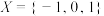 .若存在
.若存在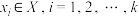 ,使得
,使得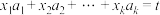 ,则称
,则称 为
为 可表数,称集合
可表数,称集合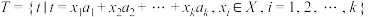 为
为 可表集.
可表集.(1)若
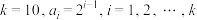 ,判定31,1024是否为
,判定31,1024是否为 可表数,并说明理由;
可表数,并说明理由;(2)若
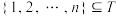 ,证明:
,证明: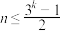 ;
;(3)设
 ,若
,若 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-01-20更新
|
1490次组卷
|
8卷引用:北京市昌平区2024届高三上学期期末质量抽测数学试题
北京市昌平区2024届高三上学期期末质量抽测数学试题江西省南昌市第二中学2024届高三“九省联考”考后适应性测试数学试题(三)(已下线)专题1 集合新定义题(九省联考第19题模式)练北京市海淀区北京一零一中2023-2024学年高三下学期统考四(开学考)数学试题广东省梅州市大埔县虎山中学2023-2024学年高二下学期开学质量检测数学试卷河南省信阳市新县高级中学2024届高三考前第五次适应性考试数学试题广东省广州市广雅中学2024届高三下学期教学情况检测(二)数学试题(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)



