名校
1 . 在某项比赛中,7位专业评委和7位观众评委分别给选手打分.针对某位选手,下面是两组评委的打分:
(1)选择一个可以度量每一组评分相似性的量,据此判断哪一组分数更可能是专业评委打的分数;
(2)现从 组评委所打分数中随机抽取2个分数,记为
组评委所打分数中随机抽取2个分数,记为 ,
, ,从
,从 组评委所打分数中随机抽取2个分数,记为
组评委所打分数中随机抽取2个分数,记为 ,
, .记事件
.记事件 ,
, 中有一个数据为48,事件
中有一个数据为48,事件 或
或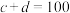 ,判断事件
,判断事件 与事件
与事件 是否相互独立
是否相互独立
| 42 | 45 | 48 | 53 | 52 | 47 | 49 |
| 48 | 52 | 70 | 66 | 77 | 49 | 51 |
(2)现从
 组评委所打分数中随机抽取2个分数,记为
组评委所打分数中随机抽取2个分数,记为 ,
, ,从
,从 组评委所打分数中随机抽取2个分数,记为
组评委所打分数中随机抽取2个分数,记为 ,
, .记事件
.记事件 ,
, 中有一个数据为48,事件
中有一个数据为48,事件 或
或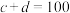 ,判断事件
,判断事件 与事件
与事件 是否相互独立
是否相互独立
您最近一年使用:0次
2 . 2024年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅游城市中的“顶流”.某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是__________ .

您最近一年使用:0次
2024-02-21更新
|
1512次组卷
|
10卷引用:重庆市渝西中学2023-2024学年高二下学期6月月考数学试题
重庆市渝西中学2023-2024学年高二下学期6月月考数学试题重庆市南开中学校2023-2024学年高三第六次质量检测(2月)数学试题黑龙江省双鸭山市第一中学2023-2024学年高二下学期开学考试数学试题(已下线)高二下学期期中复习填空题压轴题十五大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)模块五 专题1 全真基础模拟1吉林省长春外国语学校2023-2024学年高二下学期4月月考数学试卷福建省同安第一中学2023-2024学年高二下学期第1次月考(4月)数学试卷江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期期中考试数学试题河南省濮阳市第一高级中学2023-2024学年高二下学期5月期中质量检测数学试题湖南省衡阳市第八中学2024届高三下学期适应考试数学试题
名校
解题方法
3 . 月相是指天文学中对于地球上看到的月球被太阳照亮部分的称呼.1854年,爱尔兰学者在大英博物馆所藏的一块巴比伦泥板上发现了一个记录连续15天月相变化的数列,记为 ,其将满月等分成240份,
,其将满月等分成240份, (
(
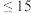 且
且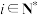 )表示第
)表示第 天月球被太阳照亮部分所占满月的份数.例如,第1天月球被太阳照亮部分占满月的
天月球被太阳照亮部分所占满月的份数.例如,第1天月球被太阳照亮部分占满月的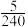 ,即
,即 ;第15天为满月,即
;第15天为满月,即 .已知
.已知 的第1项到第5项是公比为
的第1项到第5项是公比为 的等比数列,第5项到第15项是公差为
的等比数列,第5项到第15项是公差为 的等差数列,且q,d均为正整数,则
的等差数列,且q,d均为正整数,则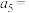 ( )
( )
 ,其将满月等分成240份,
,其将满月等分成240份, (
(
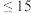 且
且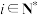 )表示第
)表示第 天月球被太阳照亮部分所占满月的份数.例如,第1天月球被太阳照亮部分占满月的
天月球被太阳照亮部分所占满月的份数.例如,第1天月球被太阳照亮部分占满月的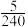 ,即
,即 ;第15天为满月,即
;第15天为满月,即 .已知
.已知 的第1项到第5项是公比为
的第1项到第5项是公比为 的等比数列,第5项到第15项是公差为
的等比数列,第5项到第15项是公差为 的等差数列,且q,d均为正整数,则
的等差数列,且q,d均为正整数,则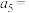 ( )
( )| A.40 | B.80 | C.96 | D.112 |
您最近一年使用:0次
2024-01-18更新
|
454次组卷
|
4卷引用:重庆市九龙坡区重庆实验外国语学校2024届高三下学期入学测试数学试题
重庆市九龙坡区重庆实验外国语学校2024届高三下学期入学测试数学试题北京市丰台区2023-2024学年高二上学期期末练习数学试卷(已下线)1.3.1等比数列的概念(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)云南省曲靖市第一中学2023-2024学年高二下学期第一次阶段性考试(3月月考)数学试题
2024·全国·模拟预测
名校
4 . 某校体育锻炼时间准备提供三项体育活动供学生选择.为了解该校学生对“三项体育活动中要有篮球”这种观点的态度(态度分为同意和不同意),随机调查了200名学生,数据如下:
单位:人
(1)能否有 的把握认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
的把握认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
(2)现有足球、篮球、跳绳供学生选择.
①若甲、乙两名学生从这三项运动中随机选一种,且他们的选择情况相互独立互不影响.已知在甲学生选择足球的前提下,两人的选择不同的概率为 .记事件
.记事件 为“甲学生选择足球”,事件B为“甲、乙两名学生的选择不同”,判断事件
为“甲学生选择足球”,事件B为“甲、乙两名学生的选择不同”,判断事件 、
、 是否独立,并说明理由.
是否独立,并说明理由.
②若该校所有学生每分钟跳绳个数 .根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
.根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
参考公式和数据: ,其中
,其中 ;
;
若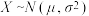 ,则
,则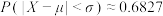 ,
,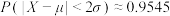 ,
, .
.
单位:人
| 男生 | 女生 | 合计 | |
| 同意 | 70 | 50 | 120 |
| 不同意 | 30 | 50 | 80 |
| 合计 | 100 | 100 | 200 |
 的把握认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?
的把握认为学生对“三项体育活动中要有篮球”这种观点的态度与性别有关?(2)现有足球、篮球、跳绳供学生选择.
①若甲、乙两名学生从这三项运动中随机选一种,且他们的选择情况相互独立互不影响.已知在甲学生选择足球的前提下,两人的选择不同的概率为
 .记事件
.记事件 为“甲学生选择足球”,事件B为“甲、乙两名学生的选择不同”,判断事件
为“甲学生选择足球”,事件B为“甲、乙两名学生的选择不同”,判断事件 、
、 是否独立,并说明理由.
是否独立,并说明理由.②若该校所有学生每分钟跳绳个数
 .根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).
.根据往年经验,该校学生经过训练后,跳绳个数都有明显进步.假设经过训练后每人每分钟跳绳个数比开始时个数增加10,该校有1000名学生,预估经过训练后该校每分钟跳182个以上人数(结果四舍五入到整数).参考公式和数据:
 ,其中
,其中 ;
; | 0.025 | 0.010 | 0.005 |
 | 5.024 | 6.635 | 7.879 |
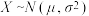 ,则
,则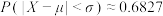 ,
,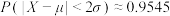 ,
, .
.
您最近一年使用:0次
2024高三·全国·专题练习
名校
5 . 某班在一次班团活动中,安排2名男生和4名女生讲演,为安排这六名学生讲演的顺序,要求两名男生之间不超过1人讲演,且第一位和最后一位出场讲演的是女生.则不同的安排方法总数为( )
| A.168 | B.192 | C.240 | D.336 |
您最近一年使用:0次
名校
6 . 新能源渗透率是指在一定时期内,新能源汽车销量占汽车总销量的比重.在2022年,新能源汽车的渗透率达到了 ,提前三年超过了“十四五”预定的
,提前三年超过了“十四五”预定的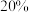 的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:
的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:
(1)假设自2023年1月起的第 个月的新能源渗透率为
个月的新能源渗透率为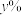 ,试求
,试求 关于
关于 的回归直线方程,并由此预测2024年1月的新能源渗透率;
的回归直线方程,并由此预测2024年1月的新能源渗透率;
(2)为了鼓励大家购买新能源汽车,国家在2024年继续执行新能源车购置税优惠政策:在2024年6月1日前购买的新能源车无需支付购置税,而燃油车需按照车价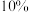 支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为
支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为 万元,求
万元,求 的分布列和期望.
的分布列和期望.
附:一组数据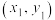 ,
,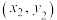 ,
,
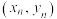 的线性回归直线方程
的线性回归直线方程 的系数公式为:
的系数公式为: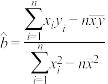 ,
,
 ,提前三年超过了“十四五”预定的
,提前三年超过了“十四五”预定的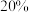 的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:
的目标.2023年,随着技术进步,新能源车的渗透率还在继续扩大.将2023年1月视为第一个月,得到2023年1-10月,我国新能源汽车渗透率如下表:月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
渗透率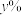 | 29 | 32 | 34 | 32 | 33 | 34 | 36 | 36 | 36 | 38 |
 个月的新能源渗透率为
个月的新能源渗透率为 ,试求
,试求 关于
关于 的回归直线方程,并由此预测2024年1月的新能源渗透率;
的回归直线方程,并由此预测2024年1月的新能源渗透率;(2)为了鼓励大家购买新能源汽车,国家在2024年继续执行新能源车购置税优惠政策:在2024年6月1日前购买的新能源车无需支付购置税,而燃油车需按照车价
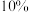 支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为
支付购置税.2024年1月小张为自己的客户代付购置税,当月他的客户购买了3辆车价格均为20万元,假设以(1)中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为 万元,求
万元,求 的分布列和期望.
的分布列和期望.附:一组数据
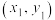 ,
,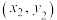 ,
,
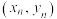 的线性回归直线方程
的线性回归直线方程 的系数公式为:
的系数公式为: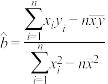 ,
,
您最近一年使用:0次
2024-01-03更新
|
987次组卷
|
5卷引用:重庆市渝西中学2023-2024学年高二下学期6月月考数学试题
重庆市渝西中学2023-2024学年高二下学期6月月考数学试题重庆市南开中学校2024届高三上学期第五次质量检测数学试题重庆市沙坪坝区南开中学校2024届高三上学期第五次质量检测数学试题陕西省渭南市澄城县2023-2024学年高二上学期期末文化课检测数学试题(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
7 . 已知 为圆锥
为圆锥 底面圆
底面圆 的直径,
的直径, ,
,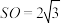 ,点
,点 为圆
为圆 上异于
上异于 的一点,
的一点, 为线段
为线段 上的动点(异于端点),则( )
上的动点(异于端点),则( )
A.直线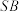 与平面 与平面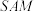 所成角的最大值为 所成角的最大值为 |
B.圆锥 内切球的体积为 内切球的体积为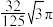 |
C.棱长为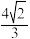 的正四面体可以放在圆锥 的正四面体可以放在圆锥 内 内 |
D.当 为 为 的中点时,满足 的中点时,满足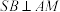 的点 的点 有2个 有2个 |
您最近一年使用:0次
2023-12-02更新
|
605次组卷
|
3卷引用:重庆市九龙坡区育才中学校2024届高三下学期阶段测试数学试题
名校
8 . 2023年7月28日,第三十一届世界大学生夏季运动会在成都隆重开幕.为庆祝大运会的到来,有 ,
, ,
, ,
, ,
, 共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.
共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.
 的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
(2)从这10人中任选3人,在这3人中恰有2人训练后为“优秀”的条件下,求这3人中恰有1人是训练前也为“优秀”的概率;
(3)跳水员 将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员
将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员 在每个高度中达到“优秀”的概率均为
在每个高度中达到“优秀”的概率均为 ,每个高度互不影响且每轮测试互不影响.如果跳水员
,每个高度互不影响且每轮测试互不影响.如果跳水员 在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?
在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?
附: ,其中
,其中 .
.
 ,
, ,
, ,
, ,
, 共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.
共10位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练.教练训练前对10位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,10位跳水员得分情况如图中实线所示,规定满分为10分,记得分在8分以上的为“优秀”.| 优秀人数 | 非优秀人数 | 合计 | |
| 训练前 | |||
| 训练后 | |||
| 合计 |
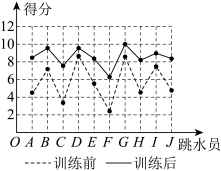
 的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;(2)从这10人中任选3人,在这3人中恰有2人训练后为“优秀”的条件下,求这3人中恰有1人是训练前也为“优秀”的概率;
(3)跳水员
 将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员
将对“5米、7.5米和10米”这三种高度进行集训,且在训练中进行了多轮测试.规定:在每轮测试中,都会有这3种高度,且至少有2个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”.每轮测试中,跳水员 在每个高度中达到“优秀”的概率均为
在每个高度中达到“优秀”的概率均为 ,每个高度互不影响且每轮测试互不影响.如果跳水员
,每个高度互不影响且每轮测试互不影响.如果跳水员 在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?
在集训测试中要想获得“优秀”的次数平均值达到3次,那么理论上至少要进行多少轮测试?附:
 ,其中
,其中 .
. | 0.05 | 0.01 | 0.005 | 0.001 |
 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2023-09-25更新
|
937次组卷
|
4卷引用:重庆市渝西中学2023-2024学年高二下学期6月月考数学试题
重庆市渝西中学2023-2024学年高二下学期6月月考数学试题湖南省师范大学附属中学2023-2024学年高三月考(六)数学试题重庆市巴蜀中学2024届高三上学期适应性月考(二)数学试题(已下线)重庆市巴蜀中学2024届高三上学期适应性月考(二)数学试题变式题19-22
名校
解题方法
9 . 某医疗科研小组为研究某市市民患有疾病 与是否具有生活习惯
与是否具有生活习惯 的关系,从该市市民中随机抽查了100人,得到如下数据:
的关系,从该市市民中随机抽查了100人,得到如下数据:
(1)依据 的独立性检验,能否认为该市市民患有疾病
的独立性检验,能否认为该市市民患有疾病 与是否具有生活习惯
与是否具有生活习惯 有关?
有关?
(2)从该市市民中任选一人, 表示事件“选到的人不具有生活习惯
表示事件“选到的人不具有生活习惯 ”,
”, 表示事件“选到的人患有疾病
表示事件“选到的人患有疾病 ”,试利用该调查数据,给出
”,试利用该调查数据,给出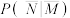 的估计值;
的估计值;
(3)从该市市民中任选3人,记这3人中具有生活习惯 ,且末患有疾病
,且末患有疾病 的人数为
的人数为 ,试利用该调查数据,给出
,试利用该调查数据,给出 的数学期望的估计值.
的数学期望的估计值.
附: ,其中
,其中 .
.
 与是否具有生活习惯
与是否具有生活习惯 的关系,从该市市民中随机抽查了100人,得到如下数据:
的关系,从该市市民中随机抽查了100人,得到如下数据:疾病 | 生活习惯 | |
| 具有 | 不具有 | |
| 患病 | 25 | 15 |
| 未患病 | 20 | 40 |
 的独立性检验,能否认为该市市民患有疾病
的独立性检验,能否认为该市市民患有疾病 与是否具有生活习惯
与是否具有生活习惯 有关?
有关?(2)从该市市民中任选一人,
 表示事件“选到的人不具有生活习惯
表示事件“选到的人不具有生活习惯 ”,
”, 表示事件“选到的人患有疾病
表示事件“选到的人患有疾病 ”,试利用该调查数据,给出
”,试利用该调查数据,给出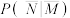 的估计值;
的估计值;(3)从该市市民中任选3人,记这3人中具有生活习惯
 ,且末患有疾病
,且末患有疾病 的人数为
的人数为 ,试利用该调查数据,给出
,试利用该调查数据,给出 的数学期望的估计值.
的数学期望的估计值.附:
 ,其中
,其中 .
.  | 0.10 | 0.05 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2023-06-21更新
|
1119次组卷
|
9卷引用:重庆市九龙坡区杨家坪中学2024届高三上学期第五次月考数学试题
重庆市九龙坡区杨家坪中学2024届高三上学期第五次月考数学试题(已下线)专题04 概率统计大题河北省衡水市第二中学2023届高三三模数学试题(已下线)专题1 全真基础模拟1(人教A版)(已下线)模块三 专题8 成对数据的统计分析--拔高能力练(人教A版)(已下线)专题1 全真基础模拟1(北师大2019版)(已下线)模块三 专题7 统计--(拔高能力练)(苏教版)(已下线)模块三 专题6 统计案例--拔高能力练(北师大2019版 高二)(已下线)重庆市巴蜀中学2024届高三上学期适应性月考(二)数学试题变式题19-22
名校
10 . 在声学中,音量被定义为: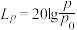 ,其中
,其中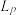 是音量(单位为dB),
是音量(单位为dB), 是基准声压为
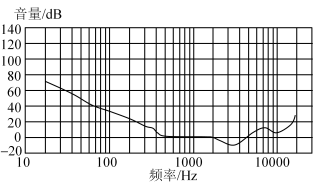
是基准声压为 ,P是实际声音压强.人耳能听到的最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频率的声音有不同的听觉下限阈值,如下图所示,其中240
,P是实际声音压强.人耳能听到的最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频率的声音有不同的听觉下限阈值,如下图所示,其中240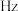 对应的听觉下限阈值为20
对应的听觉下限阈值为20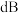 ,1000
,1000 对应的听觉下限阈值为0
对应的听觉下限阈值为0 ,则下列结论正确的是( )
,则下列结论正确的是( )
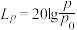 ,其中
,其中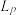 是音量(单位为dB),
是音量(单位为dB), 是基准声压为
是基准声压为 ,P是实际声音压强.人耳能听到的最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频率的声音有不同的听觉下限阈值,如下图所示,其中240
,P是实际声音压强.人耳能听到的最小音量称为听觉下限阈值.经过研究表明,人耳对于不同频率的声音有不同的听觉下限阈值,如下图所示,其中240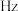 对应的听觉下限阈值为20
对应的听觉下限阈值为20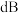 ,1000
,1000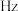 对应的听觉下限阈值为0
对应的听觉下限阈值为0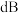 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.音量同为20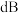 的声音,30~100 的声音,30~100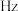 的低频比1000~10000 的低频比1000~10000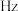 的高频更容易被人们听到. 的高频更容易被人们听到. |
| B.听觉下限阈值随声音频率的增大而减小. |
C.240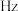 的听觉下限阈值的实际声压为0.002 的听觉下限阈值的实际声压为0.002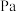 . . |
D.240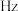 的听觉下限阈值的实际声压为1000 的听觉下限阈值的实际声压为1000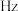 的听觉下限阈值实际声压的10倍. 的听觉下限阈值实际声压的10倍. |
您最近一年使用:0次
2023-04-06更新
|
1384次组卷
|
6卷引用:重庆市九龙坡区杨家坪中学2024届高三上学期第五次月考数学试题



