1 . 已知关于x的二次函数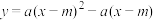 (a,m为常数,且
(a,m为常数,且 ).
).
(1)若该二次函数图象的顶点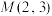 ,求a,m的值;
,求a,m的值;
(2)设该函数的图象与x轴交于A、B两点,与y轴交于点N,Q为函数图象的顶点.当 的面积与
的面积与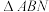 的面积相等时,求m的值.
的面积相等时,求m的值.
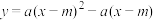 (a,m为常数,且
(a,m为常数,且 ).
).(1)若该二次函数图象的顶点
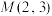 ,求a,m的值;
,求a,m的值;(2)设该函数的图象与x轴交于A、B两点,与y轴交于点N,Q为函数图象的顶点.当
 的面积与
的面积与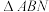 的面积相等时,求m的值.
的面积相等时,求m的值.
您最近一年使用:0次
解题方法
2 . 在长方体 中,
中,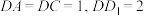 ,分别在对角线
,分别在对角线 上取点
上取点 ,使得直线
,使得直线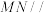 平面
平面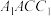 ,则线段
,则线段 长的最小值为
长的最小值为____ .
 中,
中,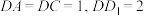 ,分别在对角线
,分别在对角线 上取点
上取点 ,使得直线
,使得直线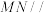 平面
平面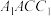 ,则线段
,则线段 长的最小值为
长的最小值为
您最近一年使用:0次
3 . 空调是人们生活水平提高的一个标志,炎热夏天,空调使温度调节到适合人们工作、学习、生活的舒适环境内,心情好,休息好,工作效率也高,这是社会进步的一个里程碑.为适应市场需求,2024年某企业扩大了某型号的变频空调的生产,全年需投入固定成本200万元,每生产x千台空调,需另投入成本 万元,当年产量不足30千台时,
万元,当年产量不足30千台时,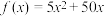 ,当年产量不小于30千台时,
,当年产量不小于30千台时,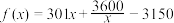 .已知每台空调售价3000元,且生产的空调能全部销售完.
.已知每台空调售价3000元,且生产的空调能全部销售完.
(1)写出年利润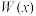 (万元)关于年产量x(千台)的函数解析式.
(万元)关于年产量x(千台)的函数解析式.
(2)年产量为多少千台时,该厂该型号的变频空调所获利润最大?并求出最大利润.
 万元,当年产量不足30千台时,
万元,当年产量不足30千台时,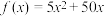 ,当年产量不小于30千台时,
,当年产量不小于30千台时,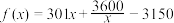 .已知每台空调售价3000元,且生产的空调能全部销售完.
.已知每台空调售价3000元,且生产的空调能全部销售完.(1)写出年利润
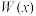 (万元)关于年产量x(千台)的函数解析式.
(万元)关于年产量x(千台)的函数解析式.(2)年产量为多少千台时,该厂该型号的变频空调所获利润最大?并求出最大利润.
您最近一年使用:0次
解题方法
4 . 设正实数 满足
满足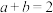 ,则( )
,则( )
 满足
满足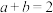 ,则( )
,则( )A.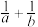 的最小值为2 的最小值为2 | B. 的最大值为 的最大值为 |
C.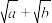 有最大值2 有最大值2 | D. 的最大值为 的最大值为 |
您最近一年使用:0次
名校
解题方法
5 . 设函数
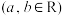 .
.
(1)若 ,函数
,函数 在
在 的值域是
的值域是 ,求函数
,求函数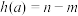 的表达式;
的表达式;
(2)令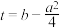 ,若存在实数
,若存在实数 ,使得
,使得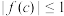 |与
|与 |同时成立,求
|同时成立,求 的取值范围
的取值范围

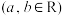 .
.(1)若
 ,函数
,函数 在
在 的值域是
的值域是 ,求函数
,求函数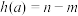 的表达式;
的表达式;(2)令
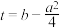 ,若存在实数
,若存在实数 ,使得
,使得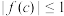 |与
|与 |同时成立,求
|同时成立,求 的取值范围
的取值范围
您最近一年使用:0次
名校
解题方法
6 . 已知函数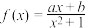 是定义在R上的奇函数,且
是定义在R上的奇函数,且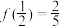
(1)求 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)设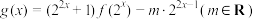 ,当
,当 时,试求函数
时,试求函数 的最大值
的最大值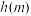 .
.
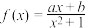 是定义在R上的奇函数,且
是定义在R上的奇函数,且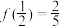
(1)求
 的解析式;
的解析式;(2)用定义证明
 在
在 上是增函数;
上是增函数;(3)设
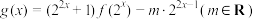 ,当
,当 时,试求函数
时,试求函数 的最大值
的最大值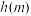 .
.
您最近一年使用:0次
2024-03-06更新
|
238次组卷
|
2卷引用:浙江省杭州四中下沙校区2023-2024学年高一上学期期中数学试题
解题方法
7 . 已知 ,
, ,且
,且 ,则( )
,则( )
 ,
, ,且
,且 ,则( )
,则( )A.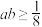 | B.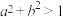 |
C.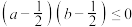 | D.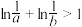 |
您最近一年使用:0次
名校
解题方法
8 . 已知 ,
, 且
且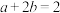 ,则( )
,则( )
 ,
, 且
且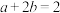 ,则( )
,则( )A.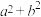 的最小值为 的最小值为 | B.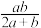 的最大值为 的最大值为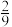 |
C.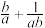 的最小值为 的最小值为 | D.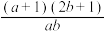 的最小值为8 的最小值为8 |
您最近一年使用:0次
名校
解题方法
9 . 如果函数 的定义域为
的定义域为 ,且存在实常数
,且存在实常数 ,使得对定义域内的任意
,使得对定义域内的任意 ,都有
,都有 恒成立,那么称此函数具有“
恒成立,那么称此函数具有“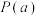 性质”.
性质”.
(1)已知 具有“
具有“ 性质”,且当
性质”,且当 时,
时, ,求
,求 在
在 的最大值;
的最大值;
(2)已知定义在 上的函数
上的函数 具有“
具有“ 性质”,当
性质”,当 时,
时, .若函数
.若函数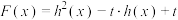 有8个零点,求实数
有8个零点,求实数 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,且存在实常数
,且存在实常数 ,使得对定义域内的任意
,使得对定义域内的任意 ,都有
,都有 恒成立,那么称此函数具有“
恒成立,那么称此函数具有“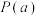 性质”.
性质”.(1)已知
 具有“
具有“ 性质”,且当
性质”,且当 时,
时, ,求
,求 在
在 的最大值;
的最大值;(2)已知定义在
 上的函数
上的函数 具有“
具有“ 性质”,当
性质”,当 时,
时, .若函数
.若函数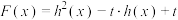 有8个零点,求实数
有8个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-24更新
|
336次组卷
|
7卷引用:浙江省温州市乐清中学2023-2024学年高一上学期期中数学试题
浙江省温州市乐清中学2023-2024学年高一上学期期中数学试题浙江省浙南名校联盟2023-2024学年高一上学期期中联考数学试题(已下线)第8章 函数应用综合能力测试-【帮课堂】(苏教版2019必修第一册)(已下线)江西省南昌市第二中学2023-2024学年高一上学期第二次月考数学试题江西省南昌市第二中学2023-2024学年高一上学期12月月考数学试题江苏省扬州市新华中学2023-2024学年高一下学期4月月考数学试题(已下线)数学(广东专用)-新高二上学期数学开学摸底考试卷
名校
解题方法
10 . 已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,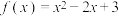 .
.
(1)求 在
在 上的取值范围;
上的取值范围;
(2)求 的函数关系式;
的函数关系式;
(3)设 ,若对于任意
,若对于任意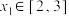 ,都存在
,都存在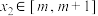 ,使得
,使得 ,求正数
,求正数 的取值范围.
的取值范围.
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,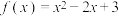 .
.(1)求
 在
在 上的取值范围;
上的取值范围;(2)求
 的函数关系式;
的函数关系式;(3)设
 ,若对于任意
,若对于任意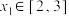 ,都存在
,都存在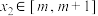 ,使得
,使得 ,求正数
,求正数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-23更新
|
365次组卷
|
2卷引用:浙江省丽水市三校联考2023-2024学年高一上学期12月月考数学试题



