名校
解题方法
1 . 记所有非零向量构成的集合为 ,对于
,对于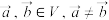 ,定义
,定义 ,
,
(1)若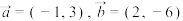 ,求出集合
,求出集合 中的三个元素;
中的三个元素;
(2)若 ,其中
,其中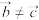 ,求证:一定存在实数
,求证:一定存在实数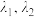 ,且
,且 ,使得
,使得 .
.
 ,对于
,对于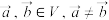 ,定义
,定义 ,
,(1)若
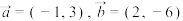 ,求出集合
,求出集合 中的三个元素;
中的三个元素;(2)若
 ,其中
,其中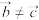 ,求证:一定存在实数
,求证:一定存在实数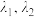 ,且
,且 ,使得
,使得 .
.
您最近一年使用:0次
2023-11-07更新
|
497次组卷
|
11卷引用:北京市清华大学附属中学奥森分校2023-2024学年高二上学期期中考试数学试题
北京市清华大学附属中学奥森分校2023-2024学年高二上学期期中考试数学试题(已下线)第9章 平面向量 单元综合检测(难点)-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)模块一 专题1 《平面向量的概念与运算》(人教A2019版)B【练】(已下线)模块二 专题1 平面向量相关概念的易混易错问题(已下线)模块三 专题2 专题1 平面向量运算(已下线)模块一 专题1《平面向量的概念与运算》单元检测篇B提升卷(苏教版高一)(已下线)模块二 专题1 平面向量相关概念的易混易错问题(苏教版)(已下线)模块三 专题2 解答题分类练 专题1 平面向量运算(解答题)(苏教版)(已下线)模块二 专题3 平面向量相关概念的易混易错问题(北师大版)(已下线)模块三 专题2 解答题分类练 专题3 平面向量各类运算(解答题)(已下线)模块一 专题3《平面向量的概念与运算》单元检测篇B提升卷(北师大版高一期中)
名校
解题方法
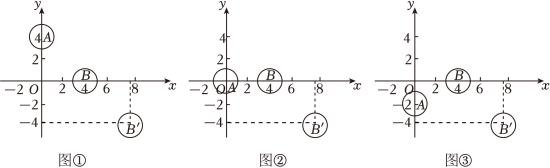
2 . 规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置.我们说球A是指该球的球心点A.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为1的圆,且母球与目标球有公共点时,目标球就开始运动.如图:在桌面上建立平面直角坐标系,设母球A的位置为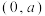 (
(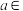 R),目标球B的位置为
R),目标球B的位置为 ,球
,球 的位置为
的位置为 ,解决下列问题:
,解决下列问题:
(1)如图①,若 ,沿向量
,沿向量 的方向击打母球A,能否使目标球B向球
的方向击打母球A,能否使目标球B向球 的球心方向运动?判断并说明理由;
的球心方向运动?判断并说明理由;
(2)如图②,若 ,要使目标球B向球
,要使目标球B向球 的球心方向运动,求母球A的球心运动的直线方程;
的球心方向运动,求母球A的球心运动的直线方程;
(3)如图③,若 ,能否让母球A击打目标球B后,使目标球B向球
,能否让母球A击打目标球B后,使目标球B向球 的球心方向运动?判断并说明理由.
的球心方向运动?判断并说明理由.
 (
(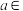 R),目标球B的位置为
R),目标球B的位置为 ,球
,球 的位置为
的位置为 ,解决下列问题:
,解决下列问题:(1)如图①,若
 ,沿向量
,沿向量 的方向击打母球A,能否使目标球B向球
的方向击打母球A,能否使目标球B向球 的球心方向运动?判断并说明理由;
的球心方向运动?判断并说明理由;(2)如图②,若
 ,要使目标球B向球
,要使目标球B向球 的球心方向运动,求母球A的球心运动的直线方程;
的球心方向运动,求母球A的球心运动的直线方程;(3)如图③,若
 ,能否让母球A击打目标球B后,使目标球B向球
,能否让母球A击打目标球B后,使目标球B向球 的球心方向运动?判断并说明理由.
的球心方向运动?判断并说明理由.
您最近一年使用:0次
解题方法
3 . 已知平面直角坐标系中,等边 的顶点坐标为
的顶点坐标为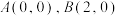 ,点
,点 在第一象限,点
在第一象限,点 是平面内任意一点.
是平面内任意一点.
(1)若 四点能构成一个平行四边形,求点
四点能构成一个平行四边形,求点 的坐标;(写出所有满足条件的情况)
的坐标;(写出所有满足条件的情况)
(2)若点 为线段
为线段 边上一动点(包含
边上一动点(包含 点),求
点),求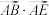 的取值范围.
的取值范围.
 的顶点坐标为
的顶点坐标为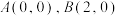 ,点
,点 在第一象限,点
在第一象限,点 是平面内任意一点.
是平面内任意一点.(1)若
 四点能构成一个平行四边形,求点
四点能构成一个平行四边形,求点 的坐标;(写出所有满足条件的情况)
的坐标;(写出所有满足条件的情况)(2)若点
 为线段
为线段 边上一动点(包含
边上一动点(包含 点),求
点),求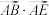 的取值范围.
的取值范围.
您最近一年使用:0次
2023-07-17更新
|
249次组卷
|
3卷引用:北京市顺义区2022-2023学年高一下学期期末质量监测数学试题
北京市顺义区2022-2023学年高一下学期期末质量监测数学试题(已下线)专题01平面向量线性、数量积运算4种常考题型归类-《期末真题分类汇编》(北京专用)【北京专用】专题07平面向量(第三部分)-高一下学期名校期末好题汇编
名校
4 . 在平面直角坐标系 中,已知点
中,已知点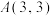 ,
,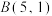 ,
,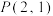 ,点
,点 是直线
是直线 上的一个动点.
上的一个动点.
(1)求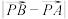 的值;
的值;
(2)若四边形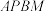 是平行四边形,求点
是平行四边形,求点 的坐标;
的坐标;
(3)求 的最小值.
的最小值.
 中,已知点
中,已知点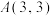 ,
,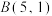 ,
,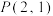 ,点
,点 是直线
是直线 上的一个动点.
上的一个动点.(1)求
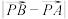 的值;
的值;(2)若四边形
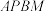 是平行四边形,求点
是平行四边形,求点 的坐标;
的坐标;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2023-01-19更新
|
780次组卷
|
2卷引用:北京市海淀区北京交通大学附属中学2021-2022学年高一下学期3月月考数学试题
名校
解题方法
5 . 如图,在△ABC中 ,点E是CD的中点,AE与BC相交于F,设
,点E是CD的中点,AE与BC相交于F,设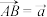 ,
,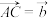 .
. ,
, 表示
表示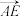 ,
,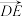 ;
;
(2)若在平面直角坐标系xOy中,已知点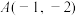 ,
,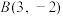 ,
,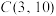 ,求
,求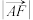 .
.
 ,点E是CD的中点,AE与BC相交于F,设
,点E是CD的中点,AE与BC相交于F,设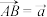 ,
,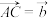 .
.
 ,
, 表示
表示 ,
, ;
;(2)若在平面直角坐标系xOy中,已知点
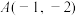 ,
,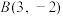 ,
,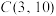 ,求
,求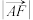 .
.
您最近一年使用:0次
2022-07-10更新
|
2763次组卷
|
10卷引用:北京市通州区运河中学2022-2023学年高一下学期3月月考数学试题
北京市通州区运河中学2022-2023学年高一下学期3月月考数学试题湖北省部分市州2021-2022学年高一下学期7月期末联考数学试题(已下线)第09讲 平面向量加、减、数乘运算的坐标表示(已下线)期末专题04 平面向量大题综合-【备战期末必刷真题】湖北省黄冈市黄梅国际育才高级中学2022-2023学年高一下学期5月月考数学试题辽宁省沈阳市东北育才学校科学高中部2022-2023学年高一上学期期末数学试题专题02平面向量基本定理与平面向量的坐标表示(已下线)高一下学期期中复习解答题压轴题十八大题型专练(1)-举一反三系列(人教A版2019必修第二册)辽宁省重点中学沈阳市郊联体2023-2024学年高一下学期4月联考数学试题(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(1)-举一反三系列(人教A版2019必修第二册)
6 . 已知点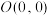 ,向量
,向量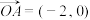 ,
,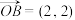 ,
,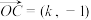 .
.
(1)若A, ,
, 三点共线,求实数
三点共线,求实数 的值;
的值;
(2)求与 垂直的单位向量的坐标;
垂直的单位向量的坐标;
(3)若点 在线段
在线段 的延长线上,且
的延长线上,且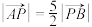 ,求点
,求点 的坐标.
的坐标.
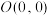 ,向量
,向量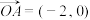 ,
,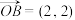 ,
,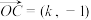 .
.(1)若A,
 ,
, 三点共线,求实数
三点共线,求实数 的值;
的值;(2)求与
 垂直的单位向量的坐标;
垂直的单位向量的坐标;(3)若点
 在线段
在线段 的延长线上,且
的延长线上,且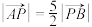 ,求点
,求点 的坐标.
的坐标.
您最近一年使用:0次
2022-05-14更新
|
586次组卷
|
2卷引用:北京市通州区2021-2022学年高一下学期期中质量检测数学试题
7 . 在平面直角坐标系中,O为坐标原点,梯形ABCD的四个顶点分别为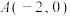 ,
,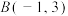 ,
, ,
,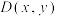 ,且
,且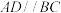 .
.
(1)若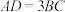 ,求点D的坐标;
,求点D的坐标;
(2)若 ,求点D的坐标;
,求点D的坐标;
(3)若点P是平面内任意一点,且 ,写出
,写出 的最大值.(只需写出结论)
的最大值.(只需写出结论)
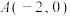 ,
,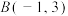 ,
, ,
,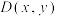 ,且
,且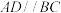 .
.(1)若
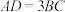 ,求点D的坐标;
,求点D的坐标;(2)若
 ,求点D的坐标;
,求点D的坐标;(3)若点P是平面内任意一点,且
 ,写出
,写出 的最大值.(只需写出结论)
的最大值.(只需写出结论)
您最近一年使用:0次

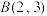 ,
,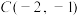 .
. 为邻边的平行四边形两条对角线的长;
为邻边的平行四边形两条对角线的长; 为何值时,
为何值时,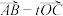 与
与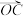 垂直;
垂直;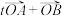 与
与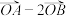 平行,平行时它们是同向还是反向.
平行,平行时它们是同向还是反向.


