名校
解题方法
1 . 《易经》是中华民族智慧的结晶,易有太极,太极生两仪,两仪生四象,四象生八卦,易经包含了深刻的哲理.如图所示是八卦模型图以及根据八卦图抽象得到的正八边形 ,其中
,其中 为正八边形的中心,则
为正八边形的中心,则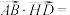
______ .

 ,其中
,其中 为正八边形的中心,则
为正八边形的中心,则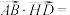

您最近一年使用:0次
2024-10-17更新
|
614次组卷
|
5卷引用:广东省江门市新会第一中学2024-2025学年高二上学期第一次质量检测数学试题
广东省江门市新会第一中学2024-2025学年高二上学期第一次质量检测数学试题广东省潮州市潮安区华南师范大学附属潮州学校2024-2025学年高二上学期开学摸底考试数学检测卷山东省七校2025届高三上学期九月联考数学试题江苏省淮阴市七校2024-2025学年高三上学期九月联考数学试卷(已下线)考点27 平面向量的运算 --高考数学100个黄金考点(2025届)【讲】
2 . 已知 ,
,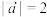 ,
, ,且
,且 与
与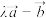 垂直,则实数
垂直,则实数 的值为 ( )
的值为 ( )
 ,
,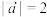 ,
, ,且
,且 与
与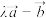 垂直,则实数
垂直,则实数 的值为 ( )
的值为 ( )A.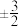 | B.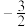 | C. | D. |
您最近一年使用:0次
2024-04-02更新
|
1188次组卷
|
35卷引用:广东省江门市新会会城华侨中学2021-2022学年高二上学期期中数学试题
广东省江门市新会会城华侨中学2021-2022学年高二上学期期中数学试题(已下线)2011-2012学年云南省会泽县茚旺高级中学高二9月月考数学试卷内蒙古翁牛特旗乌丹第二中学2017-2018学年高二12月月考数学(理)试题2018-2019人教A版高中数学选修2-1第三章 空间向量与立体几何 章末评估验收(三)(已下线)第01章+章末复习课(基础练)-2020-2021学年高二数学十分钟同步课堂专练(人教A版选择性必修第一册)人教B版(2019) 选择性必修第一册 过关斩将 第一章 空间向量与立体几何 1.1 空间向量及其运算 1.1.1 空间向量及其运算(已下线)3.5 章末复习课(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-1)西藏拉萨市那曲第二高级中学2019-2020学年高二下学期期中考试数学(文)试题河北省石家庄市藁城新冀明中学2020-2021学年高二上学期12月月考数学试题人教A版(2019) 选修第一册 实战演练 第一章 课时练习 02 空间向量的数量积运算广东省揭阳市普宁市华侨中学2021-2022学年高二下学期第三次月考数学试题河北省石家庄二十七中2023-2024学年高二上学期第一次月考数学试题山西省晋中市太谷区职业中学校2022-2023学年高二普高班上学期10月月考数学试题(已下线)山东省济南市重点中学10-11学年高一下学期期末考试数学(已下线)2012届山东省聊城莘县实验高中高三上学期期中考试数学【全国百强校】安徽省合肥一六八中学2018-2019学年高一上学期期末考试数学试题【校级联考】江西省赣州市五校协作体2018-2019学年高一下学期期中联考数学试题人教B版(2019) 必修第三册 逆袭之路 第八章 8.1 向量的数量积 8.1.2 向量数量积的运算律2020届广东省佛山市禅城区第一中学高三上学期期中数学(理)试题(已下线)6.2.4 向量的数量积(练习)-2020-2021学年下学期高一数学同步精品课堂(新教材人教版必修第二册)广东省阳山县阳山中学2021-2022学年高一下学期教学质量检测1数学试题河南省开封市2022-2023年高三上学期开学联考数学试题(已下线)第九章 平面向量(知识归纳+题型突破)2-单元速记·巧练(苏教版2019必修第二册)(已下线)广东省佛山市2024届高三教学质量检测(一)数学试题变式题7-11甘肃省酒泉市敦煌中学2023-2024学年高一下学期3月月考数学试卷天津市静海区第一中学2023-2024学年高一下学期3月学业能力调研数学试题(已下线)2.5 从力的做功到向量的数量积-同步精品课堂(北师大版2019必修第二册)(已下线)6.2.4 向量的数量积——课后作业(提升版)(已下线)第二章平面向量及其应用章末十六种常考题型归类(2)-【帮课堂】(北师大版2019必修第二册)(已下线)2.5 从力的做功到向量的数量积6种常见考法归类(1)-【帮课堂】(北师大版2019必修第二册)(已下线)高一数学期中模拟卷一(范围:平面向量+复数+立体几何初步)--同步精讲精练宝典(人教A版2019必修第二册)(已下线)专题01 平面向量-《期末真题分类汇编》(人教A版2019必修第二册)(已下线)专题03 平面向量的9种常考题型归类(2) -《期末真题分类汇编》(北师大版(2019))(已下线)专题01 平面向量重难题型(1)-期末真题分类汇编(江苏专用)新疆博湖县高级中学2023-2024学年高一下学期期中考试数学试卷
解题方法
3 . 设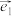 ,
,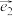 为平面内一个基底,已知向量
为平面内一个基底,已知向量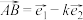 ,
,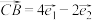 ,
,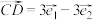 ,若A,B,D三点共线,则
,若A,B,D三点共线,则 的值是( )
的值是( )
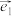 ,
,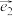 为平面内一个基底,已知向量
为平面内一个基底,已知向量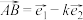 ,
,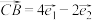 ,
,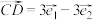 ,若A,B,D三点共线,则
,若A,B,D三点共线,则 的值是( )
的值是( )A.  | B.  | C.  | D.  |
您最近一年使用:0次
2023-08-07更新
|
207次组卷
|
8卷引用:广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题
广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题广西百色市平果市铝城中学2024-2025学年高二上学期开学收心考试数学试卷江苏省南京市江宁区2021-2022学年高一下学期期末数学试题江苏省淮阴中学教育集团涟水滨河高级中学2022-2023学年高一下学期第一次学情调研数学试题江苏省泰州市田家炳实验中学2022-2023学年高一下学期期中数学试题(已下线)9.3 向量基本定理及坐标表示1-【帮课堂】(苏教版2019必修第二册)(已下线)模块一专题2 《平面向量基本定理与坐标运算》B提升卷(苏教版)(已下线)江苏省高一下学期期末真题必刷 -期末考点大串讲(苏教版(2019))
4 . 若如图中的直线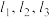 的斜率为
的斜率为 ,则( )
,则( )
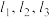 的斜率为
的斜率为 ,则( )
,则( )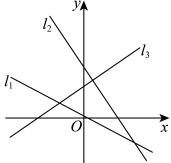
A.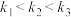 | B.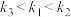 | C.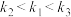 | D.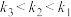 |
您最近一年使用:0次
2023-06-05更新
|
1073次组卷
|
6卷引用:广东省江门市新会区广雅中学2024-2025学年高二上学期9月月考数学试题A卷
广东省江门市新会区广雅中学2024-2025学年高二上学期9月月考数学试题A卷人教B版(2019) 选修第一册 北京名校同步练习册 第二章 平面解析几何初步 2.2直线及其方程 2.2.1直线的倾斜角与斜率(已下线)模块三 专题5 直线的倾斜角与斜率 A基础卷(已下线)第01讲 2.1.1倾斜角与斜率(8类热点题型讲练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第一册)(已下线)模块三 专题8 直线的倾斜角与斜率 A基础卷(已下线)1.1 直线的斜率与倾斜角(四大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
名校
解题方法
5 . 在 中,
中, 为
为 边上的中线,
边上的中线, 为
为 的中点,则
的中点,则 ( )
( )
 中,
中, 为
为 边上的中线,
边上的中线, 为
为 的中点,则
的中点,则 ( )
( )A.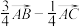 | B.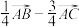 | C.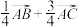 | D. |
您最近一年使用:0次
名校
解题方法
6 . 已知 ,
,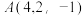 ,O为坐标原点,若
,O为坐标原点,若 ,则点B的坐标应为( )
,则点B的坐标应为( )
 ,
,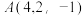 ,O为坐标原点,若
,O为坐标原点,若 ,则点B的坐标应为( )
,则点B的坐标应为( )A.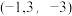 | B.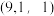 |
C.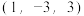 | D.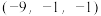 |
您最近一年使用:0次
2022-10-22更新
|
502次组卷
|
11卷引用:广东省江门市鹤山市第一中学2024-2025学年高二上学期10月月考数学试题
广东省江门市鹤山市第一中学2024-2025学年高二上学期10月月考数学试题2019年浙江省普通高中学业水平名师预测卷(一)天津市河东区2019-2020学年高二上学期期末数学试题(已下线)1.3 空间向量及其坐标的运算(精练)-2020-2021学年一隅三反系列之高二数学新教材选择性必修第一册(人教版A版)(已下线)第03讲 空间向量及其运算的坐标表示(教师版)-【帮课堂】河北省任丘市第一中学2021-2022学年高二上学期阶段考试(一)数学试题北京市首都师范大学附属密云中学2022-2023学年高二上学期阶段性练习数学试题陕西省西北农林科技大学附属中学2022-2023学年高二上学期期末理科数学试题陕西省西北农林科技大学附属中学2022-2023学年高二下学期开学考试(理科)数学试卷【随堂练】 2.3.2 空间向量运算的坐标表示 随堂练习-湘教版(2019)选择性必修第二册 第2章 空间向量与立体几何(已下线)6.3.3平面向量加减运算的坐标表示(课件+作业)
名校
解题方法
7 . 已知平面向量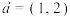 ,
,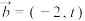 .若
.若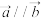 ,则
,则 ( )
( )
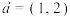 ,
,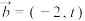 .若
.若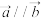 ,则
,则 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2021-11-16更新
|
1367次组卷
|
5卷引用:广东省江门市新会第一中学2024-2025学年高二上学期第一次质量检测数学试题
广东省江门市新会第一中学2024-2025学年高二上学期第一次质量检测数学试题广东省肇庆市第一中学2023-2024学年高二上学期开学考试数学试题四川省资阳市2021-2022学年高三第一次诊断考试数学(文)试题(已下线)6.2.3平面向量的坐标及其运算-2021-2022学年高一数学同步知识梳理+考点精讲精练(人教B版2019必修第二册)(已下线)期中考测试(基础)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)
8 . 刘徽(约公元225年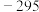 年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释.割圆术的核心思想是将一个圆的内接正
年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释.割圆术的核心思想是将一个圆的内接正 边形等分成
边形等分成 个等腰三角形,当
个等腰三角形,当 变得很大时,这些等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,得到
变得很大时,这些等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,得到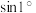 的近似值为( )
的近似值为( )
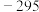 年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释.割圆术的核心思想是将一个圆的内接正
年),魏晋时期伟大的数学家,中国古代数学理论的奠基人之一.他在割圆术中提出的“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的重要阐释.割圆术的核心思想是将一个圆的内接正 边形等分成
边形等分成 个等腰三角形,当
个等腰三角形,当 变得很大时,这些等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,得到
变得很大时,这些等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,得到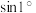 的近似值为( )
的近似值为( )A.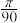 | B.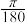 | C.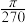 | D. |
您最近一年使用:0次
2021-07-31更新
|
790次组卷
|
5卷引用:广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题
广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题(已下线)专题5.1—任意角与弧度制-2022届高三数学一轮复习精讲精练(已下线)第02讲 弧度制-【帮课堂】2021-2022学年高一数学同步精品讲义(人教A版2019必修第一册)安徽省肥东凯悦中学2021-2022学年高一上学期第三次自主检测数学试题(已下线)第01讲 三角函数概念与诱导公式(九大题型)(练习)
名校
9 . 设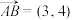 ,点
,点 的坐标为
的坐标为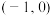 ,则点
,则点 的坐标为
的坐标为________ .
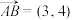 ,点
,点 的坐标为
的坐标为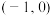 ,则点
,则点 的坐标为
的坐标为
您最近一年使用:0次
2020-06-13更新
|
796次组卷
|
12卷引用:广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题
广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题沪教版 高二年级第一学期 领航者 第八章 单元测试卷上海市行知中学2018-2019学年高二上学期期中数学试题内蒙古开鲁县第一中学2019-2020学年高一下学期期中考试数学(文)试题考点08 平面向量-2020年【衔接教材·暑假作业】新高三一轮复习数学(理)(人教版)考点09 平面向量-2020年【衔接教材·暑假作业】新高三一轮复习数学(文)(人教版)四川省成都市南开为明学校2020-2021学年高三9月月考数学(文)试题辽宁省沈阳市郊联体2020-2021学年高一下学期开学初数学试题沪教版(2020) 必修第二册 领航者 第8章 平面向量 单元测试沪教版(2020) 必修第二册 同步跟踪练习 第8章 平面向量 单元测试卷沪教版(2020) 必修第二册 领航者 一课一练 第8章 单元测试【基础卷】第8章平面向量单元测试C-沪教版(2020)必修第二册
10 . 在△ 中,
中, 为
为 边上的中线,
边上的中线, 为
为 的中点,则
的中点,则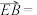
 中,
中, 为
为 边上的中线,
边上的中线, 为
为 的中点,则
的中点,则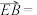
A.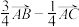 | B.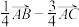 |
C. | D.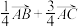 |
您最近一年使用:0次
2018-06-09更新
|
92331次组卷
|
357卷引用:广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题
广东省实验中学附属江门学校2022-2023学年高二上学期开学考试数学试题河北省临漳县第一中学2017-2018学年高二下学期第三次月考数学(文)试题【全国百强校】云南省玉溪市一中2017-2018学年高二下学期期末考试数学(理)试题云南省玉溪市一中2017-2018学年高二下学期期末考试数学(文)试题步步高高二数学暑假作业:【理】作业8 平面向量步步高高二数学暑假作业:【文】作业8 平面向量安徽省马鞍山市第二中学2019-2020学年高二上学期开学考试数学试题上海市闵行区闵行中学2019-2020学年度高二上学期期中数学试题上海市延安中学2018-2019学年高二上学期期中数学试题上海嘉定区安亭高级中学2019-2020学年高二上学期第一次月考数学试题湖南省邵阳市邵东县第一中学2019-2020学年高二下学期第一次月考数学试题浙江省金华市曙光学校2019-2020学年高二下学期返校测试数学试题浙江省杭州市2019-2020学年高二下学期期末教学质量检测数学试题山东省滕州市第一中学2020-2021学年高二9月开学收心考试数学试题湖北省宜昌市夷陵中学、荆门市钟祥一中两校2020-2021学年高二上学期10月联考数学试题广东省阳江市阳春市第一中学2020-2021学年高二上学期第三次月考数学试题重庆市三峡名校联盟2020-2021学年高二上学期联考数学试题湖南省益阳市桃江县第一中学2020-2021学年高二下学期入学考试数学试题江西省赣州市会昌县第五中学2020-2021学年高二上学期第一次月考数学(文)试题江苏省苏州市常熟市2021-2022学年高二上学期暑期自主学习调查数学试题陕西省西安市长安区第一中学2021-2022学年高二上学期9月第一次质量检测理科数学试题河北省沧州市沧县风化店中学2022-2023学年高二上学期开学考试数学试题广西贺州市钟山中学2021-2022学年高二上学期9月月考数学试题云南省大理市大理白族自治州民族中学2023-2024学年高二上学期开学考试数学试题山东省潍坊第四中学2023-2024学年高二上学期收心考试数学试题福建省泉州中远学校2022-2023学年高二高中学业水平合格性考试数学模拟试题(一)湖南省长沙市长郡中学2021-2022学年高二下学期入学考试(寒假作业检测)数学试题安徽省马鞍山市第二中学2023-2024学年高二上学期开学检测数学试题福建省龙岩市上杭县第一中学2024年6月普通高中学业水平合格性考试数学模拟卷福建省长汀县第一中学分校2023-2024学年高二下学期5月月考数学试题2018年全国普通高等学校招生统一考试理科数学(新课标I卷)2018年全国普通高等学校招生统一考试文科数学(新课标I卷)(已下线)2018年高考题及模拟题汇编 【理科】3.三角函数与平面向量江西省都昌县第一中学2019届高三上学期第一次调研考试理科数学内蒙古太仆寺旗宝昌一中2017-2018学年高一下学期期末考试数学试题(已下线)2019年一轮复习讲练测 5.1 平面向量的概念及线性运算【浙江版】【讲】2018-2019学年高中数学人教A版必修四第二章平面向量单元测试【全国百强校】宁夏石嘴山市第三中学2019届高三上学期第一次月考(开学)考试数学(文)试题【市级联考】广东省惠州市2019届高三第二次(10月)调研数学(理)试题【全国百强校】福建省福州第三中学2017-2018学年高一下学期(实验班)期末考试数学试题(已下线)2019高考热点题型和提分秘籍 【理数】专题19 平面向量的基本定理及其坐标表示( 教学案)(已下线)2019高考热点题型和提分秘籍 【文数】专题20 平面向量的数量积 (教学案)【全国百强校】贵州省黔南市都匀第一中学2018-2019学年高一上学期期末考试数学试题【校级联考】安徽省六安市毛坦厂中学、金安高级中学2018-2019学年高一上学期期末数学试题【全国百强校】北京师范大学附属中学2018-2019学年高一上学期期末考试数学试题步步高高一数学暑假作业:作业23 平面向量的线性运算山东省临沂第一中学2018-2019学年高一下学期第二次教学质量检测数学试题陕西省渭南市临渭区2018—2019学年高一第二学期期末数学试题(已下线)第01讲 平面向量的概念及线性运算(讲)-《2020年高考一轮复习讲练测》(浙江版)黑龙江省青冈县一中2018-2019高一下学期期末考试(B班)数学(文)试题人教A版 必杀技 第二章 平面向量 第二章全章训练人教A版 全能练习 必修4 第二章 第二节 2.2.3 向量数乘运算及其几何意义(已下线)专题5.1 平面向量的概念及线性运算(练)【理】—《2020年高考一轮复习讲练测》(已下线)专题5.1 平面向量的概念及线性运算(讲)【理】—《2020年高考一轮复习讲练测》内蒙古乌兰察布市北京八中乌兰察布分校2018-2019学年高一下学期四调数学试题(已下线)专题5.1 平面向量的概念及线性运算(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题5.1 平面向量的概念及线性运算(练)【文】-《2020年高考一轮复习讲练测》辽宁省沈阳市郊联体2018-2019学年高一下学期期末数学试题河北省承德市第一中学2019-2020学年高三上学期10月月考数学(理)试题2019年河北省承德市隆化县存瑞中学高三上学期第一次质检数学(文)试题福建省泉州市惠安县第十六中学2019-2020学年高三上学期期中数学(理)试题人教B版(2019) 必修第二册 过关斩将 第六章 平面向量初步 本章达标检测重庆一中2018-2019学年高一下学期期末数学试题(已下线)3.1平面向量的概念及其性质[文] -《备战2020年高考精选考点专项突破题集》(已下线)3.1平面向量的概念及其性质[理]-《备战2020年高考精选考点专项突破题集》广西柳州二中2018-2019学年高一下学期期末数学(理)试题河北省保定市定州市2018-2019学年高一上学期期末数学试题(已下线)专题5.1 平面向量的概念及线性运算(讲)-江苏版《2020年高考一轮复习讲练测》(已下线)专题5.1 平面向量的概念及线性运算(练)-江苏版《2020年高考一轮复习讲练测》山东省日照市2019-2020学年高一上学期期末校际联考数学试题人教A版(2019) 必修第二册 逆袭之路 第六章 专题一 平面向量及其运算2020届重庆市云阳江口中学校高三上学期第三次月考数学(理)试题人教B版(2019) 必修第二册 逆袭之路 第六章 专题三 高考中的平面向量问题安徽省合肥市六校2019-2020学年高一上学期期末联考数学试题人教A版(2019) 必修第二册 逆袭之路 第六章 6.2.3 向量的数乘运算江苏省苏州市张家港市外国语学校2019-2020学年高一上学期12月月考数学试题人教A版(2019) 必修第二册 过关斩将 第六章 6.3 综合拔高练山东省济宁市兖州区2018-2019学年高一下学期期中数学试题2020届湖南省长沙市长郡中学高三上学期第5次月考数学(文)试题四川省德阳市什邡中学2018-2019学年高一下学期4月月考数学试题人教A版(2019) 必修第二册 突围者 第六章 模拟高考检测河南省平顶山市2018-2019学年高一下学期期末数学试题2020届湖南省长沙市长郡中学高三第五次月考数学(文)试题重庆市云阳江口中学2020届高三上学期第一次月考数学(文)试题2020届安徽省六安市第一中学高三下学期3月月考数学(文)试题(已下线)2020届高三3月第01期(考点05)(文科)-《新题速递·数学》四川省棠湖中学2019-2020学年高一下学期第二次月考数学试题(已下线)狂刷18 平面向量的概念及线性运算-学易试题君之小题狂刷2020年高考数学(理)山东省新泰市第一中学2019-2020学年高一下学期期中考试数学试题湖北省襄阳五中2019-2020学年高一下学期网上学习3月月考数学试题四川省仁寿第二中学、华兴中学2019-2020学年高一5月联考(期中)数学试题广东省茂名地区2019-2020学年高一上学期期末数学试题(已下线)题型03 平面向量基本定理-2020届秒杀高考数学题型之平面向量宁夏银川市长庆高级中学2019-2020学年高一下学期期中考试数学试题广东省揭阳市第三中学2019-2020学年高一下学期第一次阶段考试数学试题山东省菏泽市东明县第一中学2018-2019学年高一下学期期中数学试题山东省菏泽市部分重点学校2018-2019学年高一下学期期中联考数学试题广东省深圳市第二高级中学2019-2020学年高一下学期第四学段考试数学试题陕西省榆林市绥德中学2019-2020学年高一下学期第二次阶段检测文科数学试题内蒙古开鲁县第一中学2019-2020学年高一下学期期中考试数学(文)试题陕西省榆林市绥德中学2020届高三下学期第六次模拟考试数学(文)试题江西省宜春市奉新县第一中学2019-2020学年高一下学期第二次月考数学试题湖南省娄底市第一中学2019-2020学年高一下学期期中数学试题安徽省六安市舒城中学2019-2020学年高一下学期第一次月考数学(文)试题安徽省六安市舒城中学2019-2020学年高一下学期第一次月考数学(理)试题江苏省盐城市响水中学2019-2020学年高一下学期学情分析考试(二)数学试题(已下线)专题06 平面向量-2020年高考数学(理)母题题源解密(全国Ⅲ专版)(已下线)专题11 平面向量——三年(2018-2020)高考真题文科数学分项汇编(已下线)第27讲 平面向量的概念及线性运算-2021年新高考数学一轮专题复习(新高考专版)(已下线)全册综合测试模拟一-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》山东省烟台市2019-2020学年高一下学期期末考试数学试题(已下线)专题15 平面向量的概念、线性运算、平面向量基本定理-十年(2011-2020)高考真题数学分项陕西省宝鸡市扶风县法门高中2019-2020学年高一上学期期末数学试题(已下线)考点17 平面向量的概念及其线性运算-备战2021年高考数学(文)一轮复习考点一遍过(已下线)第五单元 平面向量( A卷 基础过关检测)-2021年高考数学(文)一轮复习单元滚动双测卷广东省揭阳市产业园2019-2020学年高一下学期期末数学试题河南省项城三高2019-2020学年高一下学期第二次调研考试数学试题江西省铜鼓中学2019-2020学年度高一下学期期末测试数学试题(已下线)考点18 平面向量的概念及其线性运算-备战2021年高考数学(理)一轮复习考点一遍过海南省海南枫叶国际学校2019-2020学年高一下学期期中考试数学试题(已下线)考点18 平面向量的基本定理及坐标表示-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点15 平面向量的线性运算-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题11 平面向量——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题07 平面向量-五年(2016-2020)高考数学(文)真题分项山东省烟台市2019—2020学年度高一第二学期期末学业水平诊断数学试题(已下线)专题07 平面向量-五年(2016-2020)高考数学(理)真题分项四川省雅安市2019-2020学年高一下学期期末考试数学试题湖北省武汉市第三中学2019-2020学年高一下学期5月月考数学试题甘肃省天水市第一中学2019-2020学年高一下学期第二学段考试(期末)数学试题(已下线)考点26 平面向量的概念、平面向量的基本运算(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)专题5.1 平面向量的概念及其线性运算(精讲)-2021届高考数学(文)一轮复习讲练测陕西省咸阳市永寿中学2020-2021学年高三上学期开学考试数学(理)试题(已下线)专题5.1 平面向量的概念及其线性运算(精讲)-2021年高考数学(文)一轮复习学与练(已下线)专题6.2 平面向量的基本定理及坐标表示(精讲)-2021年新高考数学一轮复习学与练(已下线)专题6.2 平面向量的基本定理及坐标表示(讲)-2021年新高考数学一轮复习讲练测(已下线)专题6.1 平面向量的概念及其线性运算(讲)-2021年新高考数学一轮复习讲练测(已下线)专题14 平面向量-2020年高考数学(理)母题题源解密(全国Ⅰ专版)(已下线)对点练35 平面向量的概念及其线性运算-2020-2021年新高考高中数学一轮复习对点练山东省青岛市胶州市实验中学2019-2020学年第二学期高一数学期中模拟检测(三)(已下线)【新东方】杭州新东方高中数学试卷337黑龙江省八校2020-2021学年高三摸底考试数学(文)试题山西省稷山县稷山中学2020届高三上学期第二次月考数学(文)试题陕西省榆林市2020-2021学年高三上学期一模理科数学试题陕西省榆林市2020-2021学年高三上学期一模文科数学试题福建师范大学第二附属中学2020届高三上学期期中考试数学(文)试题宁夏固原市隆德县2021届高三上学期期末考试数学(理)试题(已下线)6.2.3 向量的数乘运算(分层练习)-2020-2021学年高一数学新教材配套练习(人教A版2019必修第二册)宁夏回族自治区银川市宁夏大学附属中学2021届高三上学期第四次月考数学(文)试题(已下线)专题06 平面向量(测)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题06 平面向量(测)-2021年高考数学二轮复习讲练测(文理通用)山东省滨州市2021届高三第一次模拟考试数学试题(已下线)题型03 平面向量基本定理-2021年高考数学题型秒杀之平面向量江苏省泰州中学2020-2021学年高一下学期第一次月度检测数学试题福建师范大学第二附属中学2020届高三上学期期中考试数学(理)试题(已下线)第10讲向量的概念和线性运算(练习)-【教育机构专用】2021年春季高一数学辅导讲义(沪教版2020必修第二册)(已下线)专题05 平面向量-备战2021年高考数学(文)纠错笔记(已下线)专题6.2向量基本定理与向量的坐标(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教B版)福建省福州市闽江口联盟校2021届高三上学期期中联考数学试题广东省广州市执信中学2019-2020学年高一上学期期末数学试题(已下线)数学-2021年高考考前20天终极冲刺攻略(二)(新高考地区专用)【学科网名师堂】 (5月23日)(已下线)预测06 平面向量-【临门一脚】2021年高考数学三轮冲刺过关(新高考专用)【学科网名师堂】江苏省常州市田家炳高级中学2020-2021学年高一下学期3月月考数学试题(已下线)第二章 平面向量【专项训练】-2020-2021学年高一数学下学期期末专项复习(人教A版必修4)江苏省连云港市赣榆智贤中学2020-2021学年高一下学期3月月考数学试题江苏省镇江市丹阳高级中学2020-2021学年高一(1-16班)下学期3月大练数学试题福建省福州市永泰县永泰城关中学2020-2021学年高一下学期第一次月考数学试题福建省福州市福清市西山学校2020-2021学年高一3月月考数学试题福建省厦门双十中学2020-2021学年高一下学期期中考试数学试题湖南省常德市临澧县第一中学2020-2021学年高一下学期期末数学试题河北省唐山市第十一中学2020-2021学年高一下学期期中数学试题云南省昆明市第八中学2020-2021学年高一下学期期中考试数学试题重庆市万州第二高级中学2020-2021学年高一下学期期中数学试题(已下线)解密09 平面向量(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练广东省湛江市第二十一中学2020-2021学年高一下学期期中数学试题河南省开封市五县联考2020-2021学年高一下学期期末数学试题(已下线)文科数学-2021年高考考前20天终极冲刺攻略(一)(课标全国卷) 江苏省宿迁市2020-2021学年高一下学期期末数学试题上海市南洋中学2020-2021学年高一下学期5月月考数学试题河北省唐山市曹妃甸区第一中学2020-2021学年高一下学期六月月考数学试题重庆市实验中学2020-2021学年高一下学期第一阶段测试数学试题河北省廊坊市三河市第一中学2020-2021学年高一下学期第一次阶段考数学试题福建省连城县第一中学2020-2021学年高一下学期第二次月考数学试卷江苏省苏州市(新区一中、苏大附中、苏州五中)2020-2021学年高一下学期期中联考数学试题重庆市川维中学2020-2021学年高一下学期第一次月考数学试题江苏省盐城市滨海县八滩中学2020-2021学年高一下学期期中模拟数学试题海南省北京师范大学万宁附中2020-2021学年高一下学期期中考试数学试题安徽省合肥市六校联考2020-2021学年高一下学期期末数学试题湖北省武汉市钢城第四中学2020-2021学年高一下学期期中数学试题广西防城港市防城中学2020-2021学年高一下学期期中考试数学试题山东省济南市第一中学2020-2021学年高一下学期期中数学试题宁夏银川市贺兰县景博中学2020-2021学年高一下学期期中考试数学试题江苏省宿迁市沭阳县2020-2021学年高一下学期期中数学试题海南省白沙黎族自治县白沙中学2020-2021学年高一下学期期中考试数学试题江苏省常州市武进区礼嘉中学2020-2021学年高一下学期第二次阶段质量调研数学试题云南省昭通市昭阳第一中学2020-2021学年高一12月月考数学(理)试题江苏省淮安市涟水县第一中学2020-2021学年高一下学期第一次阶段检测数学试题海南省三亚华侨学校(南新校区)2020-2021学年高一下学期3月月考数学试题(已下线)第22讲 平面向量的概念及其线性运算(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)考向23 平面向量的概念及线性运算(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)(已下线)考点16 平面向量的概念及其线性运算-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点17 平面向量的基本定理及向量坐标运算-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点18 平面向量的概念及其线性运算-备战2022年高考数学(理)一轮复习考点帮北师大版(2019) 必修第二册 金榜题名 进阶篇 十七 从速度的倍数到向量的数乘(已下线)专题06 向量与解三角形-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)考点17 平面向量的概念及其线性运算-备战2022年高考数学(文)一轮复习考点帮(已下线)第8章 平面向量(章节易错题型分析)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)(已下线)考点34 平面向量的概念与线性运算-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)专题6.1 平面向量的概念及其运算(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题6.2 平面向量的基本定理及坐标表示(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)第六章 平面向量及其应用综合测评(备作业)-【上好课】2020-2021学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)专题22 平面向量的基本定理的应用-备战2022年高考数学一轮复习一网打尽之重点难点突破宁夏青铜峡市高级中学2022届高三11月测试数学(文)试题重庆市江津第五中学校2020-2021学年高一下学期半期考试数学试题河南宋基信阳实验中学2021-2022学年高三上学期11月月考数学文科试题宁夏石嘴山市平罗中学2022届高三上学期期中考试数学(理)试题人教A版(2019) 必修第二册 实战演练 第六章 验收检测福建省德化第二中学2022届高三上学期期中考试数学试题(已下线)第27讲 平面向量基本运算及线性表示-2022年新高考数学二轮专题突破精练(已下线)考点20 平面向量的概念及线性运算、平面向量的基本定理-备战2022年高考数学典型试题解读与变式陕西省咸阳市武功县普集高中2021-2022学年高三上学期期末文科数学试题福建省福州市五校联考2022届高三上学期期中考试数学试题(已下线)数学-2022届高三下学期开学摸底考试卷(北京专用)(已下线)第6.3讲 平面向量基本定理及坐标表示-2021-2022学年高一数学链接教材精准变式练(人教A版2019必修第二册)广东省河源市龙川宏图学校2021-2022学年高一下学期月考(二)数学试题(已下线)9.3.1平面向量基本定理(备作业)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第二册)(已下线)专题06 平面向量小题大做-备战2022年高考数学冲刺横向强化精练精讲(已下线)第05讲 平面向量基本定理-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)(已下线)第六章 检测一(向量的运算)-【高效课堂】2021-2022学年高一数学下学期同步精讲课件+课后巩固练(人教A版2019必修第二册)江苏省如皋中学、丹阳高级中学、泗阳致远中学2021-2022学年高一上学期创新班12月联考数学试题福建省三明第一中学2021-2022学年高一下学期第一次月考数学试题湖北省武汉市部分重点中学2021-2022学年高一下学期3月联考数学试题山东省临沂第一中学2021-2022学年高一下学期第一次教学检测(线上)数学试题(已下线)专题34文科数学高考真题重组模拟测试(二)-备战2022年高考数学冲刺横向强化精练精讲(已下线)6.3.1 平面向量基本定理(课时作业)-2021-2022学年高一数学同步精品课件+课时作业(人教A版2019必修第二册)重庆市凤鸣山中学2021-2022学年高一下学期第一次月考数学试题(已下线)专题53 盘点平面向量问题——备战2022年高考数学二轮复习常考点专题突破重庆市二0三中学2021-2022学年高一下学期3月月考数学试题(已下线)专题1 平面向量的概念及线性运算、平面向量的基本定理-学会解题之高三数学321训练体系【2022版】福建省宁化第一中学2021-2022学年高一下学期第一次阶段考试数学试题上海市七宝中学2021-2022学年高一下学期3月月考数学试题山西省晋中市现代双语学校2021-2022学年高一下学期三月份阶段考试数学试题湖南省长沙市雅礼中学2021-2022学年高一下学期期中数学试题广东省佛山市顺德区乐从中学2021-2022学年高一下学期期中数学试题陕西省西安中学2022届高三下学期八模文科数学试题江西省南昌县莲塘第一中学2021-2022学年高一4月期中线上质量检测数学试题甘肃省兰州市教育局第四片区2021-2022学年高一下学期期中考试数学试题北京市清华大学附属中学朝阳学校2021-2022学年高一5月月考数学试题宁夏银川一中2022届高三下学期考前热身训练数学(文)试题四川省成都市实验外国语学校2021-2022学年高一下学期第一次阶段性考试数学试题黑龙江省哈尔滨市第三中学校2021-2022学年高一下学期第一次验收数学试题吉林省长春市农安县2021-2022学年高一下学期学情调研数学试题内蒙古乌兰浩特第一中学2022届高三全真模拟文科数学试题天津市第一中学2021-2022学年高一下学期期末数学试题福建省莆田华侨中学2022届高三上学期第二次月考数学试题(已下线)专题09 平面向量(已下线)专题09 平面向量-1(已下线)第34讲 平面向量的概念与线性运算-备战2023年高考数学一轮复习考点帮(新高考专用)苏教版(2019) 必修第二册 必杀技 第9章 平面向量 素养检测苏教版(2019) 必修第二册 过关斩将 第9章 9.1-9.2综合拔高练(已下线)第35讲 平面向量的基本定理与坐标运算(已下线)第01讲 平面向量(讲)(已下线)7.1 平面向量的线性运算、基本定理和坐标运算陕西省延安市第一中学2021-2022学年高一下学期期中数学试题广东省深圳市高级中学2023届高三上学期第一次调研数学试题(已下线)考向17 平面向量的概念及线性运算(重点) - 1(已下线)考向17 平面向量的概念及线性运算(重点)-2湖南省常德市临澧县第一中学2022-2023学年高三上学期第三次阶段性考试数学试题云南省昆明市第三中学2023届高三上学期10月月考数学学科能力测试试题北京市第五中学2022-2023学年高一(领航班)上学期第一次阶段检测数学试题山东省临沂市莒南县莒南第一中学2022-2023学年高一上学期9月月考数学试题广东省深圳市福田区外国语高级中学2023届高三上学期第二次调研数学试题江苏省镇江市句容碧桂园学校2022-2023学年高三上学期期中模拟数学试题北京市翔宇中学2023届高三上学期期中考试数学试题江西省南昌市第八中学2023届高三上学期11月月考数学(文)试题广东省普宁市华美实验学校2023届高三上学期第二次月考数学试题四川省内江市威远中学校2022-2023学年高三上学期第三次月考数学(文)试题四川省内江市威远中学校2022-2023学年高三上学期第三次月考数学(理)试题浙江省丽水市青田县船寮高级中学2021-2022学年高一下学期第二次月考数学试题陕西省西安市高新第一中学2021-2022学年高一上学期期末数学试题广西百色市百色民族高级中学2021-2022学年高一下学期素质拓展数学试题沪教版(2020) 一轮复习 堂堂清 第六单元 6.1 向量的概念及运算人教A版(2019) 必修第二册 必杀技 第6章 素养检测(已下线)6.2.3向量的数乘运算(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)第01讲 平面向量的概念及线性运算4种题型(2)陕西省延安市宝塔区第四中学2020-2021学年高一下学期期末数学试题四川省眉山市眉山实验高级中学2021-2022学年高三上学期12月月考数学理科试题江苏省常州市三河口高级中学2022-2023学年高一下学期3月第一次阶段测试数学试题河南省郑州市黄河科技学院附属中学2022-2023学年高一下学期3月份月考数学试题宁夏银川市第二中学2022-2023学年高一下学期月考一数学试题江苏省盐城市大丰区南阳中学2022-2023学年高一下学期第一次学情检测数学试题河北省石家庄市二中2022-2023学年高一下学期第一次月考数学试题.广东省肇庆市第一中学2022-2023学年高一下学期期中数学试题陕西省宝鸡市金台区2022-2023学年高一下学期期中数学试题山东省青岛市青岛二中分校2022-2023学年高一下学期期中考试数学试题(已下线)微专题02 平面向量的基本定理(1)-【微专题】2022-2023学年高一数学常考点微专题提分精练(人教A版2019必修第二册)(已下线)高一下期末模拟测试卷一-【单元测试】(苏教版2019必修第二册)甘肃省兰州市教育局第四片区2022-2023学年高一下学期联片办学期中考试数学试题江苏省镇江市实验高级中学、茅以升中学2022-2023学年高一下学期期中联考数学试题1.4向量的分解与坐标表示(一)第六章 平面向量初步 单元检测卷-2022-2023学年高一上学期数学人教B版(2019)必修第二册陕西省榆林市定边县第四中学2022-2023学年高一下学期期中数学试题(已下线)微点1 平面向量等和线定理及其应用(一)(1)山东省泰安肥城市2022-2023学年高一下学期期中考试数学试题广东省佛山市禅城实验高级中学2022-2023学年高一下学期第一次段考数学试题湖北省黄冈市黄州中学(黄冈外校)2022-2023学年高一下学期第五次阶段性测试数学试题广西玉林市第十一中学2022-2023学年高一下学期3月月考数学试题福建省福州市鼓楼区福州黎明中学2022-2023学年高一下学期期中数学试题湖北省黄冈市黄梅县黄梅国际育才高级中学2022-2023学年高一下学期3月月考数学试题安徽省滁州市定远县育才学校2022-2023学年高一下学期期中数学试题四川省南充市嘉陵第一中学2022-2023学年高一下学期期中数学试题广西壮族自治区贵港市平南县平南县中学2024届高三上学期9月月考数学试题广东仲元中学2024届高三上学期9月月考数学试题北京市第五中学2024届高三上学期10月月考数学试题四川省绵阳南山中学实验学校2023-2024学年高三上学期10月月考(一诊模拟)理科数学试题甘肃省平凉市泾川县第三中学2024届高三上学期第三次月考数学试题甘肃省白银市会宁县第四中学2024届高三上学期第一次月考数学试题青海省玉树藏族自治州第二民族高级中学2023-2024学年高三上学期第一次月考(10月)数学试题宁夏石嘴山市平罗中学2024届高三上学期第三次月考数学(文)试题陕西省西安市鄠邑区第二中学2024届高三上学期第三次检测数学(文)试题辽宁省葫芦岛市2023-2024学年高一上学期1月普通高中学业质量监测考试数学试题(已下线)6.2.3向量的数乘运算【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题03 向量的数乘(1)-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题9.2 向量的加减及数乘运算-重难点突破及混淆易错规避(苏教版2019必修第二册)(已下线)考点1 平面向量的概念及线性运算 --2024届高考数学考点总动员【讲】(已下线)专题03 向量的数乘运算(1)-《重难点题型·高分突破》云南省大理白族自治州祥云县祥云祥华中学2023-2024学年高一下学期3月月考数学试题(已下线)题型12 5类平面向量解题技巧福建省漳州市云霄第一中学2023-2024学年高一(平行班)下学期第一次月考数学试题河北省沧州市任丘市第一中学2023-2024学年高一下学期第一次阶段考试数学试题广东省梅州市梅县东山中学2023-2024学年高一下学期月考(一)数学试题广东省惠州市大亚湾区第一中学2023-2024学年高一下学期第一次月考数学试题河北省文安县第一中学2023-2024学年高一清北班下学期3月月考数学试卷山东省济宁市微山县第二中学2023-2024学年高一下学期第一次月考数学试题广东省佛山市高明区第一中学2023-2024学年高一下学期第一次大考数学试卷(已下线)6.2.3 向量的数乘运算——课后作业(巩固版)吉林省长春市十一高中2023-2024学年高一下学期4月月考数学试题(已下线)4.1 平面向量的概念及运算(高考真题素材之十年高考)四川省内江市威远中学校2023-2024学年高一下学期期中考试数学试题(已下线)专题10 平面向量(理科)-1(已下线)专题9 平面向量(文科)-1湖南省常德市第一中学2023-2024学年高一下学期期中考试数学试题山东省青岛市海尔学校2023-2024学年高一下学期期中考试数学试卷2024届福建省莆田市第一中学高三下学期5月模拟考试数学试题四川省南充市白塔中学2023-2024学年高一下学期第一次月考(3月)数学试题专题12平面向量(第一部分)专题14平面向量(第一部分)广西南宁市第一中学2023-2024学年高一下学期6月期末模拟试题新疆乌鲁木齐市第101中学2023-2024学年高一下学期第二次月考数学试卷云南省玉溪市江川区第一中学、通海县第一中学2023-2024学年高一下学期四月联考数学试卷吉林省辽源市田家炳高中五校2023-2024学年高一下学期7月期末联考数学试题山东省潍坊市安丘市青云学府2023-2024学年高一下学期期中考试数学试题内蒙古自治区赤峰第四中学2023-2024学年高一下学期5月月考数学试题江苏省淮安市淮安区2023-2024学年高一下学期期中考试数学试题 广西贵港市金田中学2023-2024学年高一下学期4月月考数学试题宁夏石嘴山市平罗县平罗中学2023-2024学年高一下学期期末考试数学试卷2024年山东省春季高考济南市第三次模拟考试数学试题(已下线)考点27 平面向量的运算 --高考数学100个黄金考点(2025届)【讲】



