1 . 在 中,已知
中,已知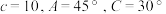 ,解这个三角形.
,解这个三角形.
 中,已知
中,已知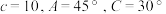 ,解这个三角形.
,解这个三角形.
您最近半年使用:0次
2024-04-10更新
|
211次组卷
|
6卷引用:北京市新学道临川学校20120-2021学年高二上学期第一次月考数学试题
北京市新学道临川学校20120-2021学年高二上学期第一次月考数学试题人教A版 成长计划 必修5 第一章正弦定理和余弦定理 第一节 1.1.1 正弦定理吉林省吉林市昌邑区吉林江城中学2019-2020学年高一下学期期末数学试题(已下线)第02讲 正弦定理-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)(已下线)第十一章 解三角形(知识归纳+题型突破)-单元速记·巧练(苏教版2019必修第二册)(已下线)专题11.2正弦定理-重难点突破及混淆易错规避(苏教版2019必修第二册)
解题方法
2 . 已知椭圆 的短轴上端点为P,过点P作椭圆互相垂直的两弦
的短轴上端点为P,过点P作椭圆互相垂直的两弦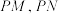 .连接
.连接 ,试求点P在
,试求点P在 上的射影Q的轨迹方程.
上的射影Q的轨迹方程.
 的短轴上端点为P,过点P作椭圆互相垂直的两弦
的短轴上端点为P,过点P作椭圆互相垂直的两弦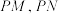 .连接
.连接 ,试求点P在
,试求点P在 上的射影Q的轨迹方程.
上的射影Q的轨迹方程.
您最近半年使用:0次
名校
3 . 将5个相同的白球和5个相同的红球全部放入3个不同的盒子中,每个盒子既要有白球,又要有红球,则不同的放球方法共有( )
| A.18种 | B.24种 | C.36种 | D.48种 |
您最近半年使用:0次
2024-04-10更新
|
1275次组卷
|
3卷引用:第七届高二试题(B卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
解题方法
4 . 已知点 ,过点P向直线
,过点P向直线 :
: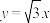 和
和 :
: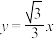 作垂线,垂足分别为点M,N,则线段MN的长是( )
作垂线,垂足分别为点M,N,则线段MN的长是( )
 ,过点P向直线
,过点P向直线 :
: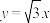 和
和 :
: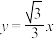 作垂线,垂足分别为点M,N,则线段MN的长是( )
作垂线,垂足分别为点M,N,则线段MN的长是( )A. | B. | C.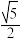 | D.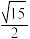 |
您最近半年使用:0次
解题方法
5 . 已知双曲线C: ,B是右顶点,F是右焦点,点A在x轴的正半轴上,且
,B是右顶点,F是右焦点,点A在x轴的正半轴上,且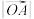 、
、 和
和 成等比数列,过点F作双曲线C在第一、三象限的渐近线的垂线l,垂足为点P.
成等比数列,过点F作双曲线C在第一、三象限的渐近线的垂线l,垂足为点P.
(1)求证: .
.
(2)若l与双曲线C的左右两支分别相交于点D、E,求双曲线的离心率e的取值范围.
 ,B是右顶点,F是右焦点,点A在x轴的正半轴上,且
,B是右顶点,F是右焦点,点A在x轴的正半轴上,且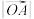 、
、 和
和 成等比数列,过点F作双曲线C在第一、三象限的渐近线的垂线l,垂足为点P.
成等比数列,过点F作双曲线C在第一、三象限的渐近线的垂线l,垂足为点P.(1)求证:
 .
.(2)若l与双曲线C的左右两支分别相交于点D、E,求双曲线的离心率e的取值范围.
您最近半年使用:0次
解题方法
6 . 已知抛物线C: ,过点
,过点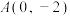 的直线l交抛物线于P、Q两点,以OP、OQ为邻边作平行四边形OPRQ.
的直线l交抛物线于P、Q两点,以OP、OQ为邻边作平行四边形OPRQ.
(1)求点R的轨迹方程.
(2)是否存在l,使四边形OPRQ为正方形?证明你的结论.
 ,过点
,过点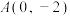 的直线l交抛物线于P、Q两点,以OP、OQ为邻边作平行四边形OPRQ.
的直线l交抛物线于P、Q两点,以OP、OQ为邻边作平行四边形OPRQ.(1)求点R的轨迹方程.
(2)是否存在l,使四边形OPRQ为正方形?证明你的结论.
您最近半年使用:0次
名校
解题方法
7 . 若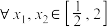 ,都有
,都有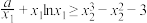 成立,则实数
成立,则实数 的取值范围是( ).
的取值范围是( ).
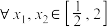 ,都有
,都有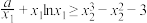 成立,则实数
成立,则实数 的取值范围是( ).
的取值范围是( ).A.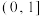 | B.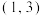 | C. | D. |
您最近半年使用:0次
2024-04-10更新
|
453次组卷
|
2卷引用:第十四届高二试题(B卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
名校
解题方法
8 . 若函数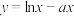 的增区间为
的增区间为 ,则
,则 的值为
的值为______ .
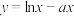 的增区间为
的增区间为 ,则
,则 的值为
的值为
您最近半年使用:0次
2024-04-10更新
|
1278次组卷
|
2卷引用:第七届高二试题(B卷)-“枫叶新希望杯”全国数学大赛真题解析(高中版)
解题方法
9 . 已知O,A,B,C四点均在半径为 的球S的表面上,并且满足
的球S的表面上,并且满足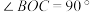 ,
, 平面
平面 ,
,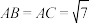 ,则三棱锥
,则三棱锥 的体积为
的体积为________ .
 的球S的表面上,并且满足
的球S的表面上,并且满足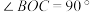 ,
, 平面
平面 ,
,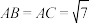 ,则三棱锥
,则三棱锥 的体积为
的体积为
您最近半年使用:0次
10 . 过曲线 :
: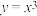 上的点
上的点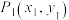 作曲线
作曲线 的切线
的切线 与曲线
与曲线 交于
交于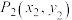 ,过点
,过点 作曲线
作曲线 的切线
的切线 与曲线
与曲线 交于点
交于点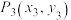 ,依此类推,可得到点列:
,依此类推,可得到点列: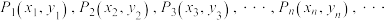 ,已知
,已知 .
.
(1)求点 ,
,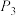 的坐标;
的坐标;
(2)求数列 的通项公式;
的通项公式;
(3)记点 到直线
到直线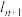 (即直线
(即直线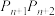 )的距离为
)的距离为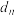 ,求证:
,求证: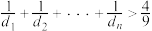 .
.
 :
: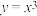 上的点
上的点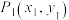 作曲线
作曲线 的切线
的切线 与曲线
与曲线 交于
交于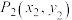 ,过点
,过点 作曲线
作曲线 的切线
的切线 与曲线
与曲线 交于点
交于点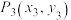 ,依此类推,可得到点列:
,依此类推,可得到点列: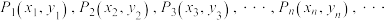 ,已知
,已知 .
.(1)求点
 ,
,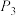 的坐标;
的坐标;(2)求数列
 的通项公式;
的通项公式;(3)记点
 到直线
到直线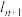 (即直线
(即直线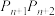 )的距离为
)的距离为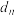 ,求证:
,求证: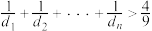 .
.
您最近半年使用:0次



