21-22高三上·上海浦东新·阶段练习
1 . 某企业为一个高科技项目注入了启动资金1000万元,已知每年可获利25%,但由于竞争激烈,每年年底需从利润中抽取200万元资金进行科研、技术改造与广告投入,方能保持原有的利润增长率,设经过n年后,该项目的资金为an万元.
(1)求a1、a2;
(2)设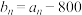 , 证明数列{bn}为等比数列,并求出至少需经过多少年,该项目的资金才可以达到或超过翻两番(即为原来的4倍)的目标(取lg2=0.3 );
, 证明数列{bn}为等比数列,并求出至少需经过多少年,该项目的资金才可以达到或超过翻两番(即为原来的4倍)的目标(取lg2=0.3 );
(3)若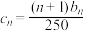 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.
(1)求a1、a2;
(2)设
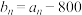 , 证明数列{bn}为等比数列,并求出至少需经过多少年,该项目的资金才可以达到或超过翻两番(即为原来的4倍)的目标(取lg2=0.3 );
, 证明数列{bn}为等比数列,并求出至少需经过多少年,该项目的资金才可以达到或超过翻两番(即为原来的4倍)的目标(取lg2=0.3 );(3)若
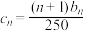 ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.
您最近一年使用:0次
2021-12-17更新
|
786次组卷
|
6卷引用:云南省曲靖市曲靖一中麒麟学校2021-2022学年高二上学期期末过关卷三(A卷)数学试题
云南省曲靖市曲靖一中麒麟学校2021-2022学年高二上学期期末过关卷三(A卷)数学试题云南省曲靖一中麒麟学校2021-2022学年高二上学期期末摸底考试数学试题上海市吴淞中学2021-2022学年高二上学期期末数学试题(已下线)上海市华东师范大学第二附属中学2022届高三上学期12月月考数学试题(已下线)2020年高考全国3数学理高考真题变式题16-20题(已下线)数学-2022届高三下学期开学摸底考试卷(上海专用)
2 . 南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列,如数列1,3,6,10,前后两项之差得到新数列2,3,4,新数列2,3,4为等差数列,这样的数列称为二阶等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为3,4,6,9,13,18,24,则该数列的第41项为 _________ .
您最近一年使用:0次
2021-12-14更新
|
685次组卷
|
4卷引用:云南省曲靖一中麒麟学校2021-2022学年高二上学期期末摸底考试数学试题
云南省曲靖一中麒麟学校2021-2022学年高二上学期期末摸底考试数学试题(已下线)专题3.1 选修一+选修二第四章数列(易)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)黑龙江省实验中学2021-2022学年高三上学期第五次月考数学理科试题(已下线)第01讲 数列-【寒假自学课】2022年高二数学寒假精品课(人教A版2019选择性必修第二册)
3 . 已知数列 的前
的前 项积为
项积为 ,且满足
,且满足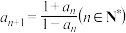 ,若
,若 ,则
,则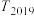 为( )
为( )
 的前
的前 项积为
项积为 ,且满足
,且满足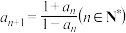 ,若
,若 ,则
,则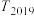 为( )
为( )| A.-4 | B.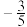 | C. | D. |
您最近一年使用:0次
4 . 对于函数 ,部分x与y的对应关系如表:
,部分x与y的对应关系如表:
数列 满足:
满足: ,且对于任意
,且对于任意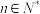 ,点
,点 都在函数
都在函数 的图象上,则
的图象上,则 ( )
( )
 ,部分x与y的对应关系如表:
,部分x与y的对应关系如表:| x | …… | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | …… |
| y | …… | 3 | 7 | 5 | 9 | 6 | 1 | 8 | 2 | 4 | …… |
 满足:
满足: ,且对于任意
,且对于任意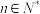 ,点
,点 都在函数
都在函数 的图象上,则
的图象上,则 ( )
( )| A.7576 | B.7575 | C.7579 | D.7564 |
您最近一年使用:0次
5 . 已知数列 的前
的前 项和为
项和为 ,
, ,
, .
.
(Ⅰ)求数列 的前
的前 项和为
项和为 ;
;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)令 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为 ,
, ,
, .
.(Ⅰ)求数列
 的前
的前 项和为
项和为 ;
;(Ⅱ)求数列
 的通项公式;
的通项公式;(Ⅲ)令
 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
解题方法
6 . 设 为数列
为数列 的前n项和,且
的前n项和,且 ,则
,则 =( )
=( )
 为数列
为数列 的前n项和,且
的前n项和,且 ,则
,则 =( )
=( )| A.26 | B.19 | C.11 | D.9 |
您最近一年使用:0次
2021-08-15更新
|
908次组卷
|
4卷引用:云南省丽江市2021-2022学年高二上学期期末质量监测数学(理)试题
7 . 在①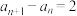 ,
, ;②
;② ;③
;③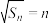 三个条件中任选一个,补充到下面问题中,并解答.
三个条件中任选一个,补充到下面问题中,并解答.
已知数列 的前
的前 项和为
项和为 ,满足______.
,满足______.
(1)求数列 的通项公式:
的通项公式:
(2)数列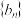 满足
满足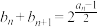 ,求数列
,求数列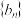 的前10项和.
的前10项和.
注:若选择不同的条件分别解答,则按第一个解答计分.
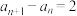 ,
, ;②
;② ;③
;③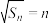 三个条件中任选一个,补充到下面问题中,并解答.
三个条件中任选一个,补充到下面问题中,并解答.已知数列
 的前
的前 项和为
项和为 ,满足______.
,满足______.(1)求数列
 的通项公式:
的通项公式:(2)数列
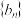 满足
满足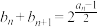 ,求数列
,求数列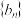 的前10项和.
的前10项和.注:若选择不同的条件分别解答,则按第一个解答计分.
您最近一年使用:0次
2021-07-31更新
|
402次组卷
|
2卷引用:云南省昆明市2020-2021学年高二下学期期末数学(理)试题
8 . 在①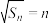 ;②
;② ;③
;③ 三个条件中任选一个,补充到下面问题中,并解答.
三个条件中任选一个,补充到下面问题中,并解答.
已知数列 的前n项和为
的前n项和为 ,满足_______.
,满足_______.
(1)求数列 的通项公式;
的通项公式;
(2)数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和 .
.
注:若选择不同的条件分别解答,则按第一个解答计分.
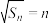 ;②
;② ;③
;③ 三个条件中任选一个,补充到下面问题中,并解答.
三个条件中任选一个,补充到下面问题中,并解答.已知数列
 的前n项和为
的前n项和为 ,满足_______.
,满足_______.(1)求数列
 的通项公式;
的通项公式;(2)数列
 满足
满足 ,求数列
,求数列 的前n项和
的前n项和 .
.注:若选择不同的条件分别解答,则按第一个解答计分.
您最近一年使用:0次
名校
解题方法
9 . 已知数列 中,
中,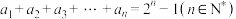 ,则
,则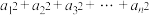 等于( )
等于( )
 中,
中,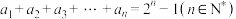 ,则
,则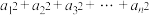 等于( )
等于( )A.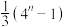 | B. | C.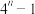 | D.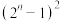 |
您最近一年使用:0次
2022-06-14更新
|
722次组卷
|
16卷引用:云南省昭通市市直中学2021-2022学年高二下学期期末数学试题
云南省昭通市市直中学2021-2022学年高二下学期期末数学试题【全国百强校】安徽省六安市第一中学2017-2018学年高一下学期期末考试数学(文)试题四川省成都市金牛区2021-2022学年高一下学期期末考试数学(理科)试题四川省成都市金牛区2021-2022学年高一下学期期末考试数学(文科)试题云南省玉溪市第一中学2023届高三上学期开学考试数学试题 河南省济源第一中学2022-2023学年高二上学期期末考试数学试题(已下线)期末精确押题之单选题(45题)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)海南省海口市第一中学2020届高三9月月考数学试题(A卷)江苏省扬州市新华中学2020-2021学年高二上学期10月阶段性测试数学试题海南省海口市第一中学2021届高三10月月考数学试题湖湘教育三新探索协作体2021-2022学年高三上学期11月期中联考数学试题(已下线)专题09 数列(选择题、填空题)-备战2022年高考数学(文)母题题源解密(全国甲卷)(已下线)专题2 等差数列与等比数列-学会解题之高三数学321训练体系【2022版】甘肃省武威市武威六中2020-2021学年高三第十次诊断考试数学(文)试题四川省内江市第二中学2022-2023学年高二上学期开学考试数学(文科)试题四川省南充市南部中学2024届高三第四次月考数学 (文)试题
名校
解题方法
10 . 已知数列 的前
的前 项和为
项和为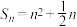 .
.
(1)求数列 的通项公式;
的通项公式;
(2)已知数列 满足
满足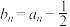 ,求
,求 的前
的前 项和.
项和.
 的前
的前 项和为
项和为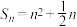 .
.(1)求数列
 的通项公式;
的通项公式;(2)已知数列
 满足
满足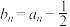 ,求
,求 的前
的前 项和.
项和.
您最近一年使用:0次
2022-01-14更新
|
491次组卷
|
3卷引用:云南省丽江市2018-2019学年高二下学期期末教学质量监测数学(文)试题



