已知函数 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(1)若 ,证明:函数
,证明:函数 的极小值为0;
的极小值为0;
(2)若存在两条直线与曲线 和曲线
和曲线 均相切,求
均相切,求 的取值范围.
的取值范围.
 ,其中
,其中 是自然对数的底数.
是自然对数的底数.(1)若
 ,证明:函数
,证明:函数 的极小值为0;
的极小值为0;(2)若存在两条直线与曲线
 和曲线
和曲线 均相切,求
均相切,求 的取值范围.
的取值范围.
22-23高三上·河南·期末 查看更多[5]
(已下线)河南省名校联盟2022-2023学年高三上学期1月新未来联考文科数学试题河南省信阳高级中学2022-2023学年高三上学期期末考试文科数学试题黑龙江省齐齐哈尔市五校联考2023-2024学年高三上学期期中考试数学试题黑龙江省齐齐哈尔市拜泉县第一中学2023-2024学年高三上学期期中考试数学试题陕西省渭南市瑞泉中学2024届高三第六次质量检测数学(文科)试题
更新时间:2023/01/15 19:59:19
|
相似题推荐
解答题-问答题
|
较难
(0.4)
【推荐1】如图, 是边长为
是边长为 的正三角形,记
的正三角形,记 位于直线
位于直线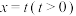 左侧的图形的面积为
左侧的图形的面积为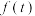 .
.

(1)求函数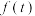 解析式;
解析式;
(2)当函数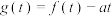 有且只有一个零点时,求
有且只有一个零点时,求 的值.
的值.
 是边长为
是边长为 的正三角形,记
的正三角形,记 位于直线
位于直线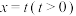 左侧的图形的面积为
左侧的图形的面积为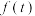 .
.
(1)求函数
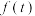 解析式;
解析式;(2)当函数
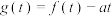 有且只有一个零点时,求
有且只有一个零点时,求 的值.
的值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知 ,函数
,函数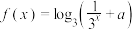 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若关于 的方程
的方程 的解集中恰有两个元素,求
的解集中恰有两个元素,求 的取值范围;
的取值范围;
(3)设 ,若对任意的
,若对任意的 ,函数
,函数 在区间
在区间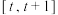 上的最大值与最小值的和不大于2,求
上的最大值与最小值的和不大于2,求 的取值范围.
的取值范围.
 ,函数
,函数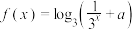 .
.(1)当
 时,解不等式
时,解不等式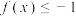 ;
;(2)若关于
 的方程
的方程 的解集中恰有两个元素,求
的解集中恰有两个元素,求 的取值范围;
的取值范围;(3)设
 ,若对任意的
,若对任意的 ,函数
,函数 在区间
在区间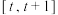 上的最大值与最小值的和不大于2,求
上的最大值与最小值的和不大于2,求 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐1】设函数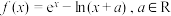 .
.
(1)当 时,求
时,求 在点
在点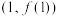 处的切线与两坐标轴围成三角形的面积;
处的切线与两坐标轴围成三角形的面积;
(2)当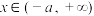 时,
时,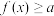 恒成立,求a的最大值.
恒成立,求a的最大值.
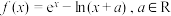 .
.(1)当
 时,求
时,求 在点
在点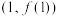 处的切线与两坐标轴围成三角形的面积;
处的切线与两坐标轴围成三角形的面积;(2)当
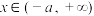 时,
时,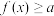 恒成立,求a的最大值.
恒成立,求a的最大值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点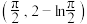 处的切线方程;
处的切线方程;
(2)讨论 在区间
在区间 上极值点个数.
上极值点个数.
 .
.(1)当
 时,求曲线
时,求曲线 在点
在点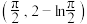 处的切线方程;
处的切线方程;(2)讨论
 在区间
在区间 上极值点个数.
上极值点个数.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】已知函数 ,
, .
.
(1)函数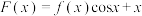 在
在 处取得极大值,求
处取得极大值,求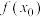 的值;
的值;
(2)若 ,证明:
,证明: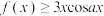 .
.
 ,
, .
.(1)函数
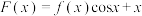 在
在 处取得极大值,求
处取得极大值,求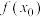 的值;
的值;(2)若
 ,证明:
,证明: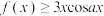 .
.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐2】已知函数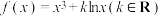 ,
, 为
为 的导函数.
的导函数.
(1)当 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2)当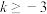 时,求证:对任意的
时,求证:对任意的 ,
, ,且
,且 ,有
,有
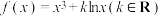 ,
, 为
为 的导函数.
的导函数.(1)当
 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;(2)当
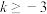 时,求证:对任意的
时,求证:对任意的 ,
, ,且
,且 ,有
,有
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐3】已知函数 .
.
(1)求函数 的极值;
的极值;
(2)设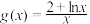 ,若对
,若对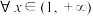 都有
都有 成立,求a的最大值.
成立,求a的最大值.
 .
.(1)求函数
 的极值;
的极值;(2)设
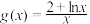 ,若对
,若对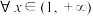 都有
都有 成立,求a的最大值.
成立,求a的最大值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】已知函数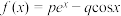 .(其中
.(其中 ,
, 为参数)在点
为参数)在点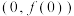 处的切线方程为
处的切线方程为 .
.
(1)求实数 ,
, 的值;
的值;
(2)求函数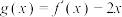 的最小值;
的最小值;
(3)若对任意的 ,不等式
,不等式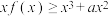 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
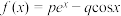 .(其中
.(其中 ,
, 为参数)在点
为参数)在点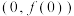 处的切线方程为
处的切线方程为 .
.(1)求实数
 ,
, 的值;
的值;(2)求函数
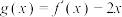 的最小值;
的最小值;(3)若对任意的
 ,不等式
,不等式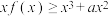 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
解题方法
【推荐2】函数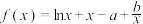 ,对任意
,对任意 ,都有
,都有 恒成立.
恒成立.
(1)当 时,求
时,求 的取值范围;
的取值范围;
(2)当 时,若所有满足题意的a,b都有
时,若所有满足题意的a,b都有 恒成立,求M的最小值.
恒成立,求M的最小值.
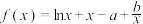 ,对任意
,对任意 ,都有
,都有 恒成立.
恒成立.(1)当
 时,求
时,求 的取值范围;
的取值范围;(2)当
 时,若所有满足题意的a,b都有
时,若所有满足题意的a,b都有 恒成立,求M的最小值.
恒成立,求M的最小值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐3】已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若关于 的方程
的方程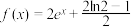 有解,求实数
有解,求实数 的取值范围.
的取值范围.
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若关于
 的方程
的方程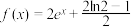 有解,求实数
有解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次

 ,不等式
,不等式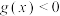 的解集为
的解集为 ,设
,设 .
.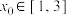 ,使不等式
,使不等式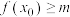 成立,求实数
成立,求实数 的取值范围;
的取值范围; 有三个不同的实数解,求实数
有三个不同的实数解,求实数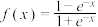 ,其定义域
,其定义域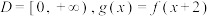 .
. 为
为 的一条切线,记其纵截距为
的一条切线,记其纵截距为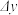 ,当
,当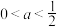 ,函数
,函数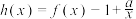 ,记
,记 的零点为
的零点为 ,求证:
,求证: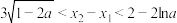 .
.


