名校
解题方法
1 . 记 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知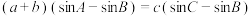 ,
, .
.
(1)求角 与
与 ;
;
(2)若点 为
为 的所在平面内一点,且满足
的所在平面内一点,且满足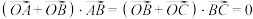 ,求
,求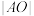 的值;
的值;
(3)若点 为
为 的重心,且
的重心,且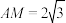 ,求
,求 的面积.
的面积.
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知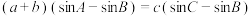 ,
, .
.(1)求角
 与
与 ;
;(2)若点
 为
为 的所在平面内一点,且满足
的所在平面内一点,且满足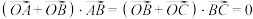 ,求
,求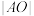 的值;
的值;(3)若点
 为
为 的重心,且
的重心,且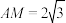 ,求
,求 的面积.
的面积.
您最近一年使用:0次
2 . 已知函数 ,
, ,若对于任意实数
,若对于任意实数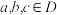 ,
,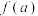 ,
, ,
,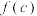 都能构成三角形的三条边长,则称函数
都能构成三角形的三条边长,则称函数 为
为 上的“完美三角形函数”.
上的“完美三角形函数”.
(1)试判断函数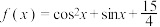 是否为
是否为 上的“完美三角形函数”,并说明理由;
上的“完美三角形函数”,并说明理由;
(2)设向量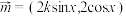 ,
, ,若函数
,若函数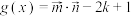 为
为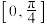 上的“完美三角形函数”,求实数
上的“完美三角形函数”,求实数 的取值范围;
的取值范围;
(3)已知函数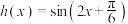 为
为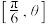 (
( 为常数)上的“完美三角形函数”.函数
为常数)上的“完美三角形函数”.函数 的图象上,是否存在不同的三个点
的图象上,是否存在不同的三个点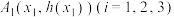 ,满足
,满足 ,
,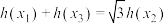 ?若存在,求
?若存在,求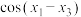 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 ,
, ,若对于任意实数
,若对于任意实数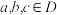 ,
,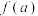 ,
, ,
,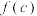 都能构成三角形的三条边长,则称函数
都能构成三角形的三条边长,则称函数 为
为 上的“完美三角形函数”.
上的“完美三角形函数”.(1)试判断函数
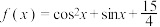 是否为
是否为 上的“完美三角形函数”,并说明理由;
上的“完美三角形函数”,并说明理由;(2)设向量
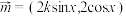 ,
, ,若函数
,若函数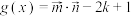 为
为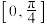 上的“完美三角形函数”,求实数
上的“完美三角形函数”,求实数 的取值范围;
的取值范围;(3)已知函数
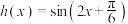 为
为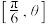 (
( 为常数)上的“完美三角形函数”.函数
为常数)上的“完美三角形函数”.函数 的图象上,是否存在不同的三个点
的图象上,是否存在不同的三个点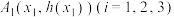 ,满足
,满足 ,
,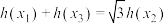 ?若存在,求
?若存在,求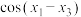 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
名校
3 . 在复平面内,复数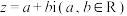 对应的点为
对应的点为 ,连接OZ(O为坐标原点)可得向量
,连接OZ(O为坐标原点)可得向量 ,则称复数z为向量
,则称复数z为向量 的对应复数,向量
的对应复数,向量 为复数z的对应向量.
为复数z的对应向量.
(1)若复数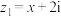 ,
,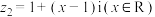 的对应向量共线,求实数x的值;
的对应向量共线,求实数x的值;
(2)已知复数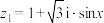 ,
,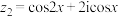 的对应向量分别为
的对应向量分别为 和
和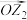 ,若
,若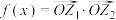 ,求
,求 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
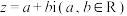 对应的点为
对应的点为 ,连接OZ(O为坐标原点)可得向量
,连接OZ(O为坐标原点)可得向量 ,则称复数z为向量
,则称复数z为向量 的对应复数,向量
的对应复数,向量 为复数z的对应向量.
为复数z的对应向量.(1)若复数
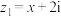 ,
,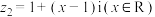 的对应向量共线,求实数x的值;
的对应向量共线,求实数x的值;(2)已知复数
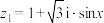 ,
,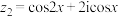 的对应向量分别为
的对应向量分别为 和
和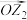 ,若
,若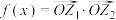 ,求
,求 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
您最近一年使用:0次
4 . 已知向量 ,
,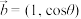 ,
, ,下列说法正确的是( )
,下列说法正确的是( )
 ,
,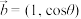 ,
, ,下列说法正确的是( )
,下列说法正确的是( )A.若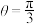 ,则向量 ,则向量 的一个单位向量是 的一个单位向量是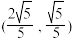 |
B.若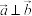 ,则 ,则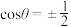 |
C.设函数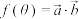 ,则 ,则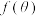 的最大值为2 的最大值为2 |
D.若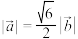 ,且 ,且 在 在 上的投影向量为 上的投影向量为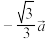 ,则 ,则 与 与 的夹角为 的夹角为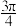 |
您最近一年使用:0次
解题方法
5 . 已知向量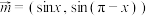 ,
,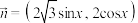 ,设
,设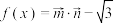 .
.
(1)求 的最小正周期;
的最小正周期;
(2)若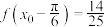 ,
,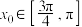 ,求
,求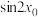 的值.
的值.
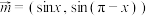 ,
,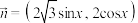 ,设
,设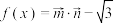 .
.(1)求
 的最小正周期;
的最小正周期;(2)若
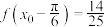 ,
,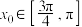 ,求
,求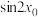 的值.
的值.
您最近一年使用:0次
7日内更新
|
288次组卷
|
2卷引用:江苏省宿迁市2023-2024学年高一下学期6月期末考试数学试题
6 .  中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设 ,
,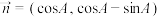 ,
,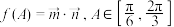 .
.
(1)求函数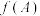 的最大值及对应的
的最大值及对应的 值;
值;
(2)若 ,求
,求 的面积
的面积
 中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设 ,
,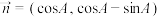 ,
,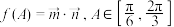 .
.(1)求函数
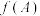 的最大值及对应的
的最大值及对应的 值;
值;(2)若
 ,求
,求 的面积
的面积
您最近一年使用:0次
7 . 已知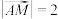 ,
,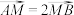 ,若动点P,Q与点A,M共面,且满足
,若动点P,Q与点A,M共面,且满足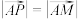 ,
, ,则
,则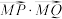 的最大值为( )
的最大值为( )
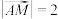 ,
,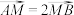 ,若动点P,Q与点A,M共面,且满足
,若动点P,Q与点A,M共面,且满足 ,
, ,则
,则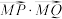 的最大值为( )
的最大值为( )| A.0 | B. | C.1 | D.2 |
您最近一年使用:0次
名校
解题方法
8 . 已知平面向量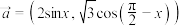 ,
,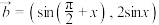 ,且函数
,且函数 .
.
(1)求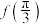 的值;
的值;
(2)求函数 的最小正周期;
的最小正周期;
(3)求函数 在
在 上的最大值,并求出取得最大值时
上的最大值,并求出取得最大值时 的值.
的值.
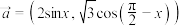 ,
,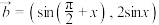 ,且函数
,且函数 .
.(1)求
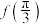 的值;
的值;(2)求函数
 的最小正周期;
的最小正周期;(3)求函数
 在
在 上的最大值,并求出取得最大值时
上的最大值,并求出取得最大值时 的值.
的值.
您最近一年使用:0次
7日内更新
|
453次组卷
|
2卷引用:浙江省2023-2024学年高二下学期6月学业水平第二次适应性联考数学试题
名校
9 . 已知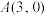 、
、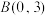 、
、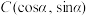 ,若
,若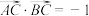 ,则
,则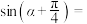 ( )
( )
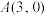 、
、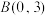 、
、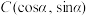 ,若
,若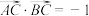 ,则
,则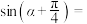 ( )
( )A. | B.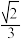 | C. | D. |
您最近一年使用:0次
解题方法
10 . 定义函数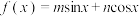 的“伴随向量”为
的“伴随向量”为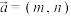 ,向量
,向量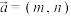 的“伴随函数”为
的“伴随函数”为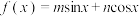 .
.
(1)若向量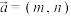 的“伴随函数”
的“伴随函数” 满足
满足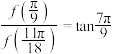 ,求
,求 的值;
的值;
(2)已知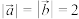 ,设
,设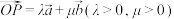 ,且
,且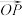 的“伴随函数”为
的“伴随函数”为 ,其最大值为t,求
,其最大值为t,求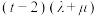 的最小值,并判断此时向量
的最小值,并判断此时向量 ,
, 的关系.
的关系.
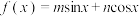 的“伴随向量”为
的“伴随向量”为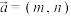 ,向量
,向量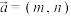 的“伴随函数”为
的“伴随函数”为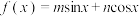 .
.(1)若向量
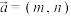 的“伴随函数”
的“伴随函数” 满足
满足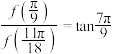 ,求
,求 的值;
的值;(2)已知
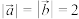 ,设
,设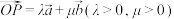 ,且
,且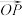 的“伴随函数”为
的“伴随函数”为 ,其最大值为t,求
,其最大值为t,求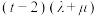 的最小值,并判断此时向量
的最小值,并判断此时向量 ,
, 的关系.
的关系.
您最近一年使用:0次



