解题方法
1 . 若 ,
, 是双曲线
是双曲线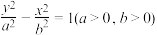 与椭圆
与椭圆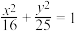 的共同焦点,点P是两曲线的一个交点,且
的共同焦点,点P是两曲线的一个交点,且 为等腰三角形,则该双曲线的渐近线方程是( )
为等腰三角形,则该双曲线的渐近线方程是( )
 ,
, 是双曲线
是双曲线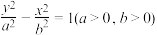 与椭圆
与椭圆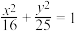 的共同焦点,点P是两曲线的一个交点,且
的共同焦点,点P是两曲线的一个交点,且 为等腰三角形,则该双曲线的渐近线方程是( )
为等腰三角形,则该双曲线的渐近线方程是( )A.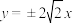 | B.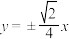 | C.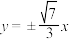 | D.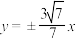 |
您最近一年使用:0次
2021-02-19更新
|
1472次组卷
|
7卷引用:江西省赣州市2021届高三上学期期末考试数学(文)试题
江西省赣州市2021届高三上学期期末考试数学(文)试题(已下线)押第11题 椭圆-备战2021年高考数学(文)临考题号押题(全国卷1)(已下线)考点39 双曲线-备战2022年高考数学(文)一轮复习考点帮(已下线)考点41 双曲线-备战2022年高考数学(理)一轮复习考点帮(已下线)解密15 双曲线方程(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)2023版 湘教版(2019) 选修第一册 过关斩将 第3章 圆锥曲线与方程(已下线)专题39 双曲线及其性质-5
解题方法
2 . 已知双曲线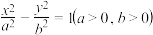 的离心率为
的离心率为 ,过右焦点且垂直于
,过右焦点且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点.点
两点.点 到双曲线的同一条渐近线的距离之和为
到双曲线的同一条渐近线的距离之和为 ,则双曲线的方程为( )
,则双曲线的方程为( )
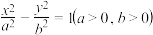 的离心率为
的离心率为 ,过右焦点且垂直于
,过右焦点且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点.点
两点.点 到双曲线的同一条渐近线的距离之和为
到双曲线的同一条渐近线的距离之和为 ,则双曲线的方程为( )
,则双曲线的方程为( )A. | B.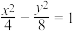 |
C. | D.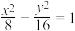 |
您最近一年使用:0次
2021-02-16更新
|
478次组卷
|
4卷引用:河南省焦作市2020-2021学年高二上学期期末数学文试题
解题方法
3 . 求经过点 ,并且对称轴都在坐标轴上的等轴双曲线的标准方程.
,并且对称轴都在坐标轴上的等轴双曲线的标准方程.
 ,并且对称轴都在坐标轴上的等轴双曲线的标准方程.
,并且对称轴都在坐标轴上的等轴双曲线的标准方程.
您最近一年使用:0次
2021-02-06更新
|
1373次组卷
|
7卷引用:人教A版(2019) 选择性必修第一册 新高考名师导学 第三章 3.2 双曲线
名校
解题方法
4 . 求适合下列条件的双曲线的标准方程.
(1)焦点在 轴上,
轴上,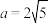 ,经过点
,经过点 ;
;
(2)经过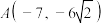 、
、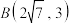 两点.
两点.
(1)焦点在
 轴上,
轴上,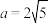 ,经过点
,经过点 ;
;(2)经过
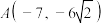 、
、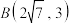 两点.
两点.
您最近一年使用:0次
2021-02-06更新
|
1172次组卷
|
5卷引用:人教A版(2019) 选择性必修第一册 新高考名师导学 第三章 3.2 双曲线
人教A版(2019) 选择性必修第一册 新高考名师导学 第三章 3.2 双曲线(已下线)专题3.2 双曲线-《讲亮点》2021-2022学年高二数学新教材同步配套讲练(苏教版2019选择性必修第一册)(已下线)3.2 双曲线海南省海口市灵山中学2021-2022学年高二上学期期末考试数学试题人教A版(2019)选择性必修第一册课本习题 习题 3.2
名校
解题方法
5 . 如图,平面上,P、Q两地间距离为4,O为PQ中点,M处为一基站,设其发射的电波为直线,测量得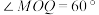 ,且O、M间距离为
,且O、M间距离为 ,现一机器人N正在运行,它在运行过程中始终保持到P地的距离比到Q地的距离大2(P、O、M、N及电波直线均共面),请建立适当的平面直角坐标系.
,现一机器人N正在运行,它在运行过程中始终保持到P地的距离比到Q地的距离大2(P、O、M、N及电波直线均共面),请建立适当的平面直角坐标系.
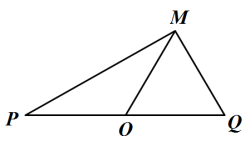
(1)求出机器人N运行的轨迹方程;
(2)为了使机器人N免受M处发射的电波的影响(即机器人接触不到过点M的直线),求出电波所在直线斜率k的取值范围.
 ,且O、M间距离为
,且O、M间距离为 ,现一机器人N正在运行,它在运行过程中始终保持到P地的距离比到Q地的距离大2(P、O、M、N及电波直线均共面),请建立适当的平面直角坐标系.
,现一机器人N正在运行,它在运行过程中始终保持到P地的距离比到Q地的距离大2(P、O、M、N及电波直线均共面),请建立适当的平面直角坐标系.
(1)求出机器人N运行的轨迹方程;
(2)为了使机器人N免受M处发射的电波的影响(即机器人接触不到过点M的直线),求出电波所在直线斜率k的取值范围.
您最近一年使用:0次
2021-02-05更新
|
196次组卷
|
2卷引用:上海市西南位育中学2020-2021学年高二上学期期末数学试题
解题方法
6 . 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
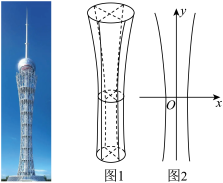

A.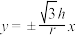 | B.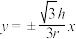 | C.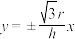 | D.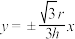 |
您最近一年使用:0次
2021-02-04更新
|
602次组卷
|
3卷引用:安徽省六安市示范高中2020-2021学年高三上学期教学质量检测数学(文)试题
安徽省六安市示范高中2020-2021学年高三上学期教学质量检测数学(文)试题安徽省六安市示范高中2020-2021学年高三上学期教学质量检测数学(理)试题(已下线)专题12 圆锥曲线的方程与性质-备战2021年高考数学(理)二轮复习题型专练?(通用版)
解题方法
7 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
,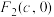 ,其渐近线方程为
,其渐近线方程为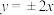 ,焦距为
,焦距为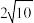 .点
.点 在双曲线
在双曲线 上,且在第一象限内,若
上,且在第一象限内,若 的面积为
的面积为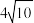 ,则点
,则点 的坐标为
的坐标为__________ .
 的左、右焦点分别为
的左、右焦点分别为 ,
,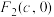 ,其渐近线方程为
,其渐近线方程为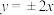 ,焦距为
,焦距为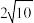 .点
.点 在双曲线
在双曲线 上,且在第一象限内,若
上,且在第一象限内,若 的面积为
的面积为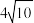 ,则点
,则点 的坐标为
的坐标为
您最近一年使用:0次
2021-02-04更新
|
161次组卷
|
2卷引用:河南省天一大联考2020-2021学年高二上学期期末考试文科数学试题
解题方法
8 . 已知双曲线 的一条渐近线的倾斜角为30°,且焦距为4,则双曲线的方程为( )
的一条渐近线的倾斜角为30°,且焦距为4,则双曲线的方程为( )
 的一条渐近线的倾斜角为30°,且焦距为4,则双曲线的方程为( )
的一条渐近线的倾斜角为30°,且焦距为4,则双曲线的方程为( )A.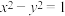 | B. | C. | D.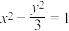 |
您最近一年使用:0次
2021-02-04更新
|
346次组卷
|
3卷引用:河南省平顶山市2020-2021学年高二上学期期末数学(理)试题
解题方法
9 . 与椭圆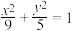 焦点相同且经过点(2,3)的双曲线的标准方程为( )
焦点相同且经过点(2,3)的双曲线的标准方程为( )
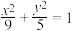 焦点相同且经过点(2,3)的双曲线的标准方程为( )
焦点相同且经过点(2,3)的双曲线的标准方程为( )A.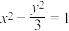 | B. | C.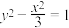 | D. |
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线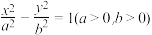 ,O为坐标原点,离心率
,O为坐标原点,离心率 ,点
,点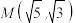 在双曲线上.
在双曲线上.
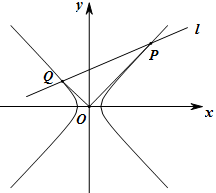
(1)求双曲线的方程
(2)如图,若直线l与双曲线的左、右两支分别交于点Q,P,且 ,求
,求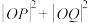 的最小值.
的最小值.
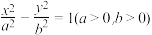 ,O为坐标原点,离心率
,O为坐标原点,离心率 ,点
,点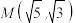 在双曲线上.
在双曲线上.
(1)求双曲线的方程

(2)如图,若直线l与双曲线的左、右两支分别交于点Q,P,且
 ,求
,求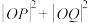 的最小值.
的最小值.
您最近一年使用:0次
2021-02-02更新
|
918次组卷
|
5卷引用:安徽省滁州市定远县重点中学2020-2021学年高二上学期期末数学(文)试题
安徽省滁州市定远县重点中学2020-2021学年高二上学期期末数学(文)试题(已下线)专题10 《圆锥曲线与方程》中的最值问题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 湖北省宜昌市英杰学校2021-2022学年高二上学期12月月月考数学试题浙江省嘉兴市第一中学2022-2023学年高三上学期期中数学试题江苏省徐宿联考2023-2024学年高二上学期第一次联考数学试题



