解题方法
1 . 已知双曲线 经过点
经过点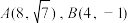 .
.
(1)求 的离心率;
的离心率;
(2)设直线 经过
经过 的右焦点,且与
的右焦点,且与 交于不同的两点
交于不同的两点 ,点N关于x轴的对称点为点P,证明:直线
,点N关于x轴的对称点为点P,证明:直线 过定点.
过定点.
 经过点
经过点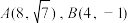 .
.(1)求
 的离心率;
的离心率;(2)设直线
 经过
经过 的右焦点,且与
的右焦点,且与 交于不同的两点
交于不同的两点 ,点N关于x轴的对称点为点P,证明:直线
,点N关于x轴的对称点为点P,证明:直线 过定点.
过定点.
您最近一年使用:0次
解题方法
2 . 已知双曲线 :
: (
( ,
, )经过点
)经过点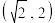 ,且其离心率为
,且其离心率为 .
.
(1)求双曲线 的方程;
的方程;
(2)设双曲线 的左,右焦点分别为
的左,右焦点分别为 ,
, ,
, 的一条渐近线上有一点
的一条渐近线上有一点 ,满足
,满足 恰好垂直于这条渐近线,求
恰好垂直于这条渐近线,求 的面积.
的面积.
 :
: (
( ,
, )经过点
)经过点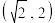 ,且其离心率为
,且其离心率为 .
.(1)求双曲线
 的方程;
的方程;(2)设双曲线
 的左,右焦点分别为
的左,右焦点分别为 ,
, ,
, 的一条渐近线上有一点
的一条渐近线上有一点 ,满足
,满足 恰好垂直于这条渐近线,求
恰好垂直于这条渐近线,求 的面积.
的面积.
您最近一年使用:0次
解题方法
3 . 已知双曲线 的顶点为椭圆
的顶点为椭圆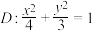 的焦点,
的焦点, 的离心率与
的离心率与 的离心率之积为1,则
的离心率之积为1,则 的方程为( )
的方程为( )
 的顶点为椭圆
的顶点为椭圆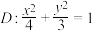 的焦点,
的焦点, 的离心率与
的离心率与 的离心率之积为1,则
的离心率之积为1,则 的方程为( )
的方程为( )A.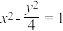 | B.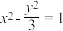 | C.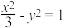 | D.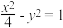 |
您最近一年使用:0次
7日内更新
|
250次组卷
|
2卷引用:河南省商丘市部分学校2023-2024学年高二下学期期末考试数学试卷
解题方法
4 . 圆锥曲线具有丰富的光学性质.双曲线的光学性质:从双曲线的一个焦点 处发出的光线,经过双曲线在点
处发出的光线,经过双曲线在点 处反射后,反射光线所在直线经过另一个焦点
处反射后,反射光线所在直线经过另一个焦点 ,且双曲线在点
,且双曲线在点 处的切线平分
处的切线平分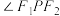 .如图,对称轴都在坐标轴上的等轴双曲线
.如图,对称轴都在坐标轴上的等轴双曲线 过点
过点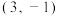 ,其左、右焦点分别为
,其左、右焦点分别为 .若从
.若从 发出的光线经双曲线右支上一点
发出的光线经双曲线右支上一点 反射的光线为
反射的光线为 ,点
,点 处的切线交
处的切线交 轴于点
轴于点 ,则下列说法正确的是( )
,则下列说法正确的是( )
 处发出的光线,经过双曲线在点
处发出的光线,经过双曲线在点 处反射后,反射光线所在直线经过另一个焦点
处反射后,反射光线所在直线经过另一个焦点 ,且双曲线在点
,且双曲线在点 处的切线平分
处的切线平分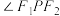 .如图,对称轴都在坐标轴上的等轴双曲线
.如图,对称轴都在坐标轴上的等轴双曲线 过点
过点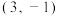 ,其左、右焦点分别为
,其左、右焦点分别为 .若从
.若从 发出的光线经双曲线右支上一点
发出的光线经双曲线右支上一点 反射的光线为
反射的光线为 ,点
,点 处的切线交
处的切线交 轴于点
轴于点 ,则下列说法正确的是( )
,则下列说法正确的是( )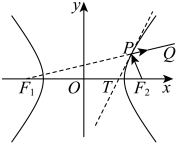
A.双曲线 的方程为 的方程为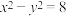 |
B.过点 且垂直于 且垂直于 的直线平分 的直线平分 |
C.若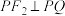 ,则 ,则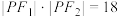 |
D.若 ,则 ,则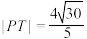 |
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
5 . 直线 与双曲线
与双曲线
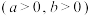 相交于
相交于 ,
, 两点,若以
两点,若以 为直径的圆过原点,且双曲线的离心率为
为直径的圆过原点,且双曲线的离心率为 ,求双曲线的方程.
,求双曲线的方程.
 与双曲线
与双曲线
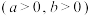 相交于
相交于 ,
, 两点,若以
两点,若以 为直径的圆过原点,且双曲线的离心率为
为直径的圆过原点,且双曲线的离心率为 ,求双曲线的方程.
,求双曲线的方程.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
6 . 过双曲线 右焦点且斜率为
右焦点且斜率为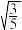 的直线
的直线 交双曲线于
交双曲线于 ,
, ,若
,若 且
且 ,求双曲线的方程.
,求双曲线的方程.
 右焦点且斜率为
右焦点且斜率为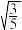 的直线
的直线 交双曲线于
交双曲线于 ,
, ,若
,若 且
且 ,求双曲线的方程.
,求双曲线的方程.
您最近一年使用:0次
解题方法
7 . 南非双曲线大教堂是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线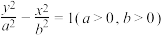 下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )
下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )
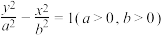 下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )
下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )

A.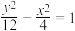 | B. | C. | D.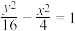 |
您最近一年使用:0次
名校
解题方法
8 . 已知双曲线 的右顶点
的右顶点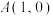 到
到 的一条渐近线的距离为
的一条渐近线的距离为 .
.
(1)求 的方程;
的方程;
(2)设过点 的直线交
的直线交 于
于 两点,过
两点,过 且垂直于
且垂直于 轴的直线与直线
轴的直线与直线 交于点
交于点 ,证明:以线段
,证明:以线段 的中点为圆心且过坐标原点的圆还过其他定点.
的中点为圆心且过坐标原点的圆还过其他定点.
 的右顶点
的右顶点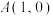 到
到 的一条渐近线的距离为
的一条渐近线的距离为 .
.(1)求
 的方程;
的方程;(2)设过点
 的直线交
的直线交 于
于 两点,过
两点,过 且垂直于
且垂直于 轴的直线与直线
轴的直线与直线 交于点
交于点 ,证明:以线段
,证明:以线段 的中点为圆心且过坐标原点的圆还过其他定点.
的中点为圆心且过坐标原点的圆还过其他定点.
您最近一年使用:0次
2024-07-15更新
|
180次组卷
|
3卷引用:山西省长治市2023-2024学年高二下学期6月期末数学试题
解题方法
9 . 与椭圆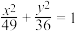 有公共焦点,且过点
有公共焦点,且过点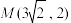 的双曲线方程为
的双曲线方程为______ .
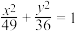 有公共焦点,且过点
有公共焦点,且过点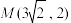 的双曲线方程为
的双曲线方程为
您最近一年使用:0次
解题方法
10 . 已知双曲线 :
: 的渐近线方程为
的渐近线方程为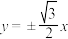 ,过点
,过点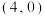 的直线
的直线 交双曲线
交双曲线 于
于 ,
, 两点,且当
两点,且当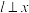 轴时,
轴时,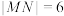 .
.
(1)求 的方程;
的方程;
(2)记双曲线 的左右顶点分别为
的左右顶点分别为 ,
, ,直线
,直线 ,
,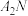 的斜率分别为
的斜率分别为 ,
, ,求
,求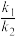 的值.
的值.
(3)探究圆 :
: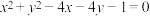 上是否存在点
上是否存在点 ,使得过
,使得过 作双曲线的两条切线
作双曲线的两条切线 ,
, 互相垂直.
互相垂直.
 :
: 的渐近线方程为
的渐近线方程为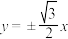 ,过点
,过点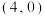 的直线
的直线 交双曲线
交双曲线 于
于 ,
, 两点,且当
两点,且当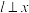 轴时,
轴时,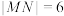 .
.(1)求
 的方程;
的方程;(2)记双曲线
 的左右顶点分别为
的左右顶点分别为 ,
, ,直线
,直线 ,
,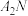 的斜率分别为
的斜率分别为 ,
, ,求
,求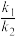 的值.
的值.(3)探究圆
 :
: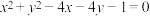 上是否存在点
上是否存在点 ,使得过
,使得过 作双曲线的两条切线
作双曲线的两条切线 ,
, 互相垂直.
互相垂直.
您最近一年使用:0次



