解题方法
1 . 已知双曲线 的焦点为
的焦点为 和
和 ,一条渐近线方程为
,一条渐近线方程为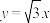 ,则
,则 的方程为
的方程为_________ .
 的焦点为
的焦点为 和
和 ,一条渐近线方程为
,一条渐近线方程为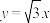 ,则
,则 的方程为
的方程为
您最近一年使用:0次
解题方法
2 . 已知双曲线 (
( ,
, )的左、右焦点分别为
)的左、右焦点分别为 ,
, ,过
,过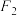 且斜率为
且斜率为 的直线与双曲线在第一象限的交点为A,若
的直线与双曲线在第一象限的交点为A,若 ,则此双曲线的标准方程可能为( )
,则此双曲线的标准方程可能为( )
 (
( ,
, )的左、右焦点分别为
)的左、右焦点分别为 ,
, ,过
,过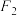 且斜率为
且斜率为 的直线与双曲线在第一象限的交点为A,若
的直线与双曲线在第一象限的交点为A,若 ,则此双曲线的标准方程可能为( )
,则此双曲线的标准方程可能为( )A.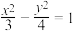 | B.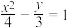 |
C. | D. |
您最近一年使用:0次
解题方法
3 . 已知点 在双曲线
在双曲线 上,且
上,且 的离心率为
的离心率为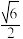 ,直线
,直线 交
交 于
于 ,
, 两点,直线
两点,直线 ,
, 的倾斜角互补.
的倾斜角互补.
(1)求直线 的倾斜角;
的倾斜角;
(2)若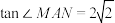 ,求
,求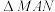 内切圆的面积.
内切圆的面积.
 在双曲线
在双曲线 上,且
上,且 的离心率为
的离心率为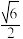 ,直线
,直线 交
交 于
于 ,
, 两点,直线
两点,直线 ,
, 的倾斜角互补.
的倾斜角互补.(1)求直线
 的倾斜角;
的倾斜角;(2)若
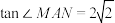 ,求
,求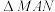 内切圆的面积.
内切圆的面积.
您最近一年使用:0次
名校
解题方法
4 . 已知A,B分别是双曲线 的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为
的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为 ,且
,且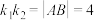 .
.
(1)求双曲线C的方程;
(2)已知过点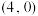 的直线
的直线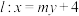 ,交C的左,右两支于D,E两点(异于A,B).
,交C的左,右两支于D,E两点(异于A,B).
(i)求m的取值范围;
(ii)设直线AD与直线BE交于点Q,求证:点Q在定直线上.
 的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为
的左、右顶点,P是C上异于A,B的一点,直线PA,PB的斜率分别为 ,且
,且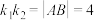 .
.(1)求双曲线C的方程;
(2)已知过点
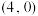 的直线
的直线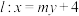 ,交C的左,右两支于D,E两点(异于A,B).
,交C的左,右两支于D,E两点(异于A,B).(i)求m的取值范围;
(ii)设直线AD与直线BE交于点Q,求证:点Q在定直线上.
您最近一年使用:0次
名校
解题方法
5 . 已知双曲线 的渐近线为
的渐近线为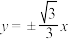 ,左顶点为
,左顶点为 .
.
(1)求双曲线 的方程;
的方程;
(2)直线 交
交 轴于点
轴于点 ,过
,过 点的直线交双曲线
点的直线交双曲线 于
于 ,
, ,直线
,直线 ,
, 分别交
分别交 于
于 ,
, ,若
,若 ,
, ,
, ,
, 均在圆
均在圆 上,
上,
①求 的值,并求点
的值,并求点 的横坐标;
的横坐标;
②求圆 面积的取值范围.
面积的取值范围.
 的渐近线为
的渐近线为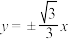 ,左顶点为
,左顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)直线
 交
交 轴于点
轴于点 ,过
,过 点的直线交双曲线
点的直线交双曲线 于
于 ,
, ,直线
,直线 ,
, 分别交
分别交 于
于 ,
, ,若
,若 ,
, ,
, ,
, 均在圆
均在圆 上,
上,①求
 的值,并求点
的值,并求点 的横坐标;
的横坐标;②求圆
 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
6 . 已知双曲线 经过点
经过点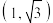 ,其一条渐近线方程为
,其一条渐近线方程为 ,则双曲线
,则双曲线 的标准方程为
的标准方程为______ ,离心率
______ .
 经过点
经过点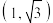 ,其一条渐近线方程为
,其一条渐近线方程为 ,则双曲线
,则双曲线 的标准方程为
的标准方程为
您最近一年使用:0次
解题方法
7 . 已知双曲线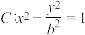 的图像经过点
的图像经过点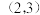 ,点
,点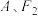 分别是双曲线
分别是双曲线 的左顶点和右焦点.设过
的左顶点和右焦点.设过 的直线
的直线 交
交 的右支于
的右支于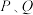 两点,其中点
两点,其中点 在第一象限.
在第一象限. 的标准方程;
的标准方程;
(2)若直线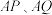 分别交直线
分别交直线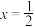 于
于 两点,证明:
两点,证明: 为定值;
为定值;
(3)是否存在常数 ,使得
,使得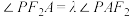 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
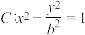 的图像经过点
的图像经过点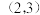 ,点
,点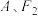 分别是双曲线
分别是双曲线 的左顶点和右焦点.设过
的左顶点和右焦点.设过 的直线
的直线 交
交 的右支于
的右支于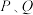 两点,其中点
两点,其中点 在第一象限.
在第一象限.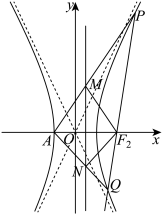
 的标准方程;
的标准方程;(2)若直线
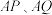 分别交直线
分别交直线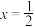 于
于 两点,证明:
两点,证明: 为定值;
为定值;(3)是否存在常数
 ,使得
,使得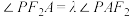 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
解题方法
8 . 已知双曲线C的标准方程为 .若虚轴长为
.若虚轴长为 ,且双曲线上的任意一点P到左右两个焦点
,且双曲线上的任意一点P到左右两个焦点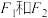 距离之差的绝对值为2.
距离之差的绝对值为2.
(1)求双曲线C的标准方程;
(2)若点 (0,1),求
(0,1),求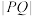 的取值范围;
的取值范围;
(3)若斜率为 的直线
的直线 过右焦点
过右焦点 ,且与C的右支相交于A、B两点,问:在x轴上是否存在定点M,使得无论直线
,且与C的右支相交于A、B两点,问:在x轴上是否存在定点M,使得无论直线 绕点
绕点 怎样转动,总有
怎样转动,总有 成立?如果存在,求出定点M的坐标;如果不存在,请说明理由.
成立?如果存在,求出定点M的坐标;如果不存在,请说明理由.
 .若虚轴长为
.若虚轴长为 ,且双曲线上的任意一点P到左右两个焦点
,且双曲线上的任意一点P到左右两个焦点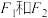 距离之差的绝对值为2.
距离之差的绝对值为2.(1)求双曲线C的标准方程;
(2)若点
 (0,1),求
(0,1),求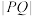 的取值范围;
的取值范围;(3)若斜率为
 的直线
的直线 过右焦点
过右焦点 ,且与C的右支相交于A、B两点,问:在x轴上是否存在定点M,使得无论直线
,且与C的右支相交于A、B两点,问:在x轴上是否存在定点M,使得无论直线 绕点
绕点 怎样转动,总有
怎样转动,总有 成立?如果存在,求出定点M的坐标;如果不存在,请说明理由.
成立?如果存在,求出定点M的坐标;如果不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
9 . 已知双曲线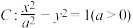 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 为双曲线上一点,且
为双曲线上一点,且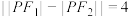
(1)求双曲线 的标准方程及其渐近线方程;
的标准方程及其渐近线方程;
(2)已知直线 与双曲线
与双曲线 交于
交于 两点,且
两点,且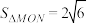 ,其中
,其中 为坐标原点,求
为坐标原点,求 的值.
的值.
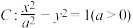 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 为双曲线上一点,且
为双曲线上一点,且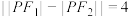
(1)求双曲线
 的标准方程及其渐近线方程;
的标准方程及其渐近线方程;(2)已知直线
 与双曲线
与双曲线 交于
交于 两点,且
两点,且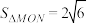 ,其中
,其中 为坐标原点,求
为坐标原点,求 的值.
的值.
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线 的离心率为2,顶点到渐近线的距离为
的离心率为2,顶点到渐近线的距离为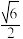 .
.
(1)求 的方程;
的方程;
(2)若直线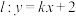 交
交 于
于 两点,
两点, 为坐标原点,且
为坐标原点,且 的面积为
的面积为 ,求
,求 的值.
的值.
 的离心率为2,顶点到渐近线的距离为
的离心率为2,顶点到渐近线的距离为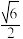 .
.(1)求
 的方程;
的方程;(2)若直线
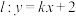 交
交 于
于 两点,
两点, 为坐标原点,且
为坐标原点,且 的面积为
的面积为 ,求
,求 的值.
的值.
您最近一年使用:0次



