1 . 已知椭圆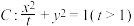 的左、右焦点分别为
的左、右焦点分别为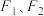 ,直线
,直线 与椭圆
与椭圆 交于
交于 两点(
两点( 点在
点在 点的上方),与
点的上方),与 轴交于点
轴交于点 .
.
(1)当 时,点
时,点 为椭圆
为椭圆 上除顶点外任一点,求
上除顶点外任一点,求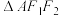 的周长;
的周长;
(2)当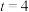 且直线
且直线 过点
过点 时,设
时,设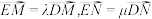 ,求证:
,求证: 为定值,并求出该值;
为定值,并求出该值;
(3)若椭圆 的离心率为
的离心率为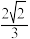 ,当
,当 为何值时,
为何值时,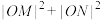 恒为定值;并求此时
恒为定值;并求此时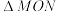 面积的最大值.
面积的最大值.
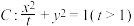 的左、右焦点分别为
的左、右焦点分别为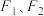 ,直线
,直线 与椭圆
与椭圆 交于
交于 两点(
两点( 点在
点在 点的上方),与
点的上方),与 轴交于点
轴交于点 .
.(1)当
 时,点
时,点 为椭圆
为椭圆 上除顶点外任一点,求
上除顶点外任一点,求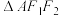 的周长;
的周长;(2)当
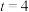 且直线
且直线 过点
过点 时,设
时,设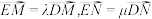 ,求证:
,求证: 为定值,并求出该值;
为定值,并求出该值;(3)若椭圆
 的离心率为
的离心率为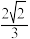 ,当
,当 为何值时,
为何值时,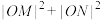 恒为定值;并求此时
恒为定值;并求此时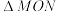 面积的最大值.
面积的最大值.
您最近半年使用:0次
名校
解题方法
2 . 在平面直角坐标系 中,已知点
中,已知点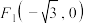 ,
,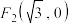 ,
,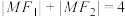 ,记
,记 的轨迹为
的轨迹为 .
.
(1)求 的方程;
的方程;
(2)过点 的直线
的直线 与
与 交于
交于 ,
, 两点,
两点,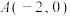 ,
,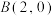 ,设直线
,设直线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
,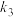 .证明:
.证明: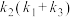 为定值.
为定值.
 中,已知点
中,已知点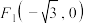 ,
,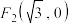 ,
,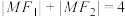 ,记
,记 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)过点
 的直线
的直线 与
与 交于
交于 ,
, 两点,
两点,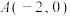 ,
,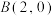 ,设直线
,设直线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
,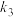 .证明:
.证明: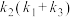 为定值.
为定值.
您最近半年使用:0次
2024高三下·全国·专题练习
3 . 已知点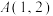 在抛物线C:
在抛物线C: 上,点P,Q是抛物线C上的两个动点(均不与A重合),直线AP,AQ的斜率分别为
上,点P,Q是抛物线C上的两个动点(均不与A重合),直线AP,AQ的斜率分别为 ,
, ,且
,且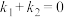 .
.
(1)求直线PQ的斜率;
(2)设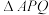 的外接圆为圆G,过点A作抛物线C的切线l,试判断直线l与圆G的位置关系,并说明理由.
的外接圆为圆G,过点A作抛物线C的切线l,试判断直线l与圆G的位置关系,并说明理由.
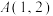 在抛物线C:
在抛物线C: 上,点P,Q是抛物线C上的两个动点(均不与A重合),直线AP,AQ的斜率分别为
上,点P,Q是抛物线C上的两个动点(均不与A重合),直线AP,AQ的斜率分别为 ,
, ,且
,且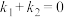 .
.(1)求直线PQ的斜率;
(2)设
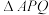 的外接圆为圆G,过点A作抛物线C的切线l,试判断直线l与圆G的位置关系,并说明理由.
的外接圆为圆G,过点A作抛物线C的切线l,试判断直线l与圆G的位置关系,并说明理由.
您最近半年使用:0次
名校
解题方法
4 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,D为椭圆C的右顶点,且
,D为椭圆C的右顶点,且 .
.
(1)求椭圆C的方程;
(2)设 ,过点
,过点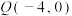 的直线与椭圆C交于A,B两点(A点在B点左侧),直线AM与直线
的直线与椭圆C交于A,B两点(A点在B点左侧),直线AM与直线 交于点N,设直线NA,NB的斜率分别为
交于点N,设直线NA,NB的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 的左、右焦点分别为
的左、右焦点分别为 ,D为椭圆C的右顶点,且
,D为椭圆C的右顶点,且 .
.(1)求椭圆C的方程;
(2)设
 ,过点
,过点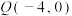 的直线与椭圆C交于A,B两点(A点在B点左侧),直线AM与直线
的直线与椭圆C交于A,B两点(A点在B点左侧),直线AM与直线 交于点N,设直线NA,NB的斜率分别为
交于点N,设直线NA,NB的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
您最近半年使用:0次
5 . 在平面直角坐标系 中,一动圆经过点
中,一动圆经过点 且与直线
且与直线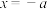 相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
(1)当 时,求曲线K的轨迹方程;
时,求曲线K的轨迹方程;
(2)已知过点A 且斜率为k的直线l与曲线K交于B,C 两点,若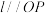 且直线
且直线 与直线
与直线 交于Q点.求证:
交于Q点.求证:  为定值:
为定值:
(3)若
 且点 D,E在y轴上,
且点 D,E在y轴上, 的内切圆的方程为
的内切圆的方程为
 求
求 面积的最小值.
面积的最小值.
 中,一动圆经过点
中,一动圆经过点 且与直线
且与直线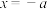 相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.
相切,设该动圆圆心的轨迹为曲线K, P是曲线K上一点.(1)当
 时,求曲线K的轨迹方程;
时,求曲线K的轨迹方程;(2)已知过点A 且斜率为k的直线l与曲线K交于B,C 两点,若
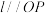 且直线
且直线 与直线
与直线 交于Q点.求证:
交于Q点.求证:  为定值:
为定值:(3)若

 且点 D,E在y轴上,
且点 D,E在y轴上, 的内切圆的方程为
的内切圆的方程为
 求
求 面积的最小值.
面积的最小值.
您最近半年使用:0次
6 . 已知椭圆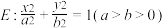 ,点
,点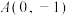 是椭圆中心与该椭圆一个顶点的中点,点
是椭圆中心与该椭圆一个顶点的中点,点 为椭圆与
为椭圆与 轴正半轴的交点,且离心率为
轴正半轴的交点,且离心率为 ,过点
,过点 的直线(与
的直线(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线 和直线
和直线 的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
(3)若圆 的方程为
的方程为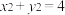 ,直线
,直线 ,
, 分别交圆
分别交圆 于
于 ,
, 两点,试证明:直线
两点,试证明:直线 恒过定点.
恒过定点.
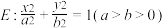 ,点
,点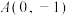 是椭圆中心与该椭圆一个顶点的中点,点
是椭圆中心与该椭圆一个顶点的中点,点 为椭圆与
为椭圆与 轴正半轴的交点,且离心率为
轴正半轴的交点,且离心率为 ,过点
,过点 的直线(与
的直线(与 轴不重合)交椭圆
轴不重合)交椭圆 于
于 ,
, 两点.
两点.(1)求椭圆
 的标准方程;
的标准方程;(2)直线
 和直线
和直线 的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;
的斜率之积是否为定值?若是,求出这个值,若不是请说明理由;(3)若圆
 的方程为
的方程为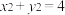 ,直线
,直线 ,
, 分别交圆
分别交圆 于
于 ,
, 两点,试证明:直线
两点,试证明:直线 恒过定点.
恒过定点.
您最近半年使用:0次
7 . 已知双曲线 的一条渐近线方程为
的一条渐近线方程为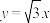 ,右焦点
,右焦点 到渐近线的距离为
到渐近线的距离为 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)过点 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,
两点, .求
.求 的值.
的值.
 的一条渐近线方程为
的一条渐近线方程为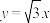 ,右焦点
,右焦点 到渐近线的距离为
到渐近线的距离为 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)过点
 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,
两点, .求
.求 的值.
的值.
您最近半年使用:0次
8 . 已知点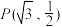 在椭圆
在椭圆 上,F为右焦点,PF垂直于x轴.A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.
上,F为右焦点,PF垂直于x轴.A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.
(1)求椭圆E的方程;
(2)设 ,
, ,满足
,满足 ,判断
,判断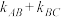 的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
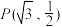 在椭圆
在椭圆 上,F为右焦点,PF垂直于x轴.A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.
上,F为右焦点,PF垂直于x轴.A,B,C,D为椭圆上四个动点,且AC,BD交于原点O.(1)求椭圆E的方程;
(2)设
 ,
, ,满足
,满足 ,判断
,判断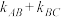 的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
的值是否为定值,若是,求出此定值,并求出四边形ABCD面积的最大值,否则请说明理由.
您最近半年使用:0次
9 . 已知曲线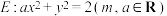 .
.
(1)当 时,若曲线
时,若曲线 交
交 轴于
轴于 、
、 两点,
两点, 为曲线
为曲线 上异于
上异于 、
、 的点,求直线
的点,求直线 、
、 的斜率之积;
的斜率之积;
(2)若直线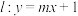 与曲线
与曲线 交于
交于 、
、 两点,
两点,
①当 时,求
时,求 面积的最大值;
面积的最大值;
②当实数 为何值时,对任意
为何值时,对任意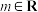 ,都有
,都有 为定值
为定值 ?并求出
?并求出 的值.
的值.
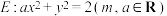 .
.(1)当
 时,若曲线
时,若曲线 交
交 轴于
轴于 、
、 两点,
两点, 为曲线
为曲线 上异于
上异于 、
、 的点,求直线
的点,求直线 、
、 的斜率之积;
的斜率之积;(2)若直线
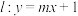 与曲线
与曲线 交于
交于 、
、 两点,
两点,①当
 时,求
时,求 面积的最大值;
面积的最大值;②当实数
 为何值时,对任意
为何值时,对任意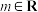 ,都有
,都有 为定值
为定值 ?并求出
?并求出 的值.
的值.
您最近半年使用:0次
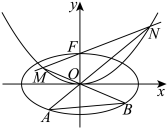
10 . 如图,已知椭圆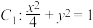 和抛物线
和抛物线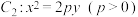 ,
, 的焦点
的焦点 是
是 的上顶点,过
的上顶点,过 的直线交
的直线交 于
于 、
、 两点,连接
两点,连接 、
、 并延长之,分别交
并延长之,分别交 于
于 、
、 两点,连接
两点,连接 ,设
,设 、
、 的面积分别为
的面积分别为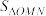 、
、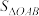 .
. 的值;
的值;
(2)求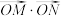 的值;
的值;
(3)求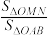 的取值范围.
的取值范围.
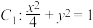 和抛物线
和抛物线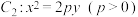 ,
, 的焦点
的焦点 是
是 的上顶点,过
的上顶点,过 的直线交
的直线交 于
于 、
、 两点,连接
两点,连接 、
、 并延长之,分别交
并延长之,分别交 于
于 、
、 两点,连接
两点,连接 ,设
,设 、
、 的面积分别为
的面积分别为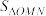 、
、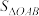 .
.
 的值;
的值;(2)求
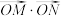 的值;
的值;(3)求
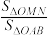 的取值范围.
的取值范围.
您最近半年使用:0次



