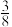名校
解题方法
1 . 设有穷数列 的项数为
的项数为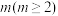 ,若正整数
,若正整数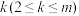 满足:
满足: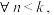
 ,则称
,则称 为数列
为数列 的“
的“ 点”.
点”.
(1)若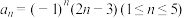 ,求数列
,求数列 的“
的“ 点”;
点”;
(2)已知有穷等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 .若数列
.若数列 存在“
存在“ 点”,求正数
点”,求正数 的取值范围;
的取值范围;
(3)若 ,数列
,数列 的“
的“ 点”的个数为
点”的个数为 ,证明:
,证明: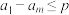 .
.
 的项数为
的项数为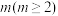 ,若正整数
,若正整数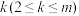 满足:
满足: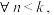
 ,则称
,则称 为数列
为数列 的“
的“ 点”.
点”.(1)若
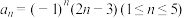 ,求数列
,求数列 的“
的“ 点”;
点”;(2)已知有穷等比数列
 的公比为
的公比为 ,前
,前 项和为
项和为 .若数列
.若数列 存在“
存在“ 点”,求正数
点”,求正数 的取值范围;
的取值范围;(3)若
 ,数列
,数列 的“
的“ 点”的个数为
点”的个数为 ,证明:
,证明: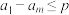 .
.
您最近一年使用:0次
今日更新
|
71次组卷
|
2卷引用:重庆市开州中学2023-2024学年高三下学期高考模拟考试数学试题(四)
名校
解题方法
2 . (1)已知函数 ,证明:
,证明: ,
, ,
,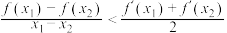 .
.
(2)已知函数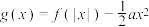 ,定义:若存在
,定义:若存在 ,
,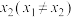 ,使得曲线
,使得曲线 在点
在点 与点
与点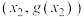 处有相同的切线
处有相同的切线 ,则称切线
,则称切线 为“自公切线”.
为“自公切线”.
①证明:当 时,曲线
时,曲线 不存在“自公切线”;
不存在“自公切线”;
②讨论曲线 的“自公切线”的条数.
的“自公切线”的条数.
 ,证明:
,证明: ,
, ,
,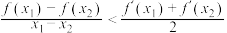 .
.(2)已知函数
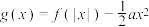 ,定义:若存在
,定义:若存在 ,
,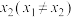 ,使得曲线
,使得曲线 在点
在点 与点
与点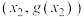 处有相同的切线
处有相同的切线 ,则称切线
,则称切线 为“自公切线”.
为“自公切线”.①证明:当
 时,曲线
时,曲线 不存在“自公切线”;
不存在“自公切线”;②讨论曲线
 的“自公切线”的条数.
的“自公切线”的条数.
您最近一年使用:0次
名校
3 . 某公司为了解年研发资金 (单位:亿元)对年产值
(单位:亿元)对年产值 (单位:亿元)的影响,对公司近8年的年研发资金
(单位:亿元)的影响,对公司近8年的年研发资金 和年产值
和年产值 (
(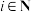 ,
,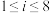 )的数据对比分析中,选用了两个回归模型,并利用最小二乘法求得相应的
)的数据对比分析中,选用了两个回归模型,并利用最小二乘法求得相应的 关于
关于 的经验回归方程:
的经验回归方程:
①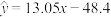 ;②
;②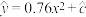 .
.
(1)求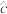 的值;
的值;
(2)已知①中的残差平方和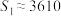 ,②中的残差平方和
,②中的残差平方和 ,请根据决定系数选择拟合效果更好的经验回归方程,并利用该经验回归方程预测年研发资金为20亿元时的年产值.
,请根据决定系数选择拟合效果更好的经验回归方程,并利用该经验回归方程预测年研发资金为20亿元时的年产值.
参考数据: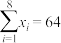 ,
,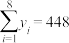 ,
,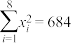 ,
,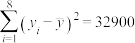 .
.
参考公式;刻画回归模型拟合效果的决定系数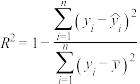 .
.
 (单位:亿元)对年产值
(单位:亿元)对年产值 (单位:亿元)的影响,对公司近8年的年研发资金
(单位:亿元)的影响,对公司近8年的年研发资金 和年产值
和年产值 (
(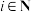 ,
,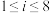 )的数据对比分析中,选用了两个回归模型,并利用最小二乘法求得相应的
)的数据对比分析中,选用了两个回归模型,并利用最小二乘法求得相应的 关于
关于 的经验回归方程:
的经验回归方程:①
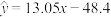 ;②
;②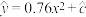 .
.(1)求
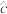 的值;
的值;(2)已知①中的残差平方和
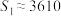 ,②中的残差平方和
,②中的残差平方和 ,请根据决定系数选择拟合效果更好的经验回归方程,并利用该经验回归方程预测年研发资金为20亿元时的年产值.
,请根据决定系数选择拟合效果更好的经验回归方程,并利用该经验回归方程预测年研发资金为20亿元时的年产值.参考数据:
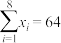 ,
,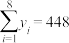 ,
,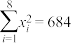 ,
,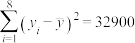 .
.参考公式;刻画回归模型拟合效果的决定系数
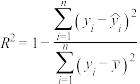 .
.
您最近一年使用:0次
名校
解题方法
4 . 设集合 (
( ),
), 为
为 的非空子集,随机变量
的非空子集,随机变量 ,
, 分别表示取到子集
分别表示取到子集 中得最大元素和最小元素的数值.
中得最大元素和最小元素的数值.
(1)若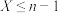 的概率为
的概率为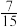 ,求
,求 ;
;
(2)若 ,求
,求 且
且 的概率;
的概率;
(3)已知:对于随机变量 ,
, ,有
,有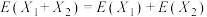 .求随机变量
.求随机变量 的均值
的均值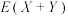 .
.
 (
( ),
), 为
为 的非空子集,随机变量
的非空子集,随机变量 ,
, 分别表示取到子集
分别表示取到子集 中得最大元素和最小元素的数值.
中得最大元素和最小元素的数值.(1)若
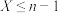 的概率为
的概率为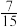 ,求
,求 ;
;(2)若
 ,求
,求 且
且 的概率;
的概率;(3)已知:对于随机变量
 ,
, ,有
,有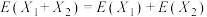 .求随机变量
.求随机变量 的均值
的均值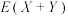 .
.
您最近一年使用:0次
名校
解题方法
5 . 2006年,在国家节能减排的宏观政策指导下,科技部在“十一五”启动了“863”计划新能源汽车重大项目.自2011年起,国家相关部门重点扶持新能源汽车的发展,也逐步得到消费者的认可.如下表是统计的2014年-2023年全国新能源汽车保有量(百万辆)数据:
并计算得: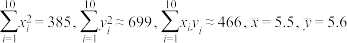 .
.
(1)根据表中数据,求相关年份与全国新能源汽车保有量的样本相关系数(精确到0.01);
(2)现苏同学购买第1辆汽车时随机在新能源汽车和非新能源汽车中选择.如果第1辆购买新能源汽车,那么第2辆仍选择购买新能源汽车的概率为0.6;如果第1辆购买非新能源汽车,那么第2辆购买新能源汽车的概率为0.8,计算苏同学第2辆购买新能源汽车的概率;
(3)某汽车网站为调查新能源汽车车主的用车体验,决定从12名候选车主中选3名车主进行访谈,已知有4名候选车主是新能源汽车车主,假设每名候选人都有相同的机会被选到,求被选到新能源汽车车主的分布列及数学期望.
附:相关系数: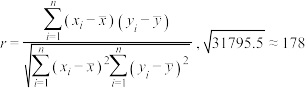 .
.
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
保有量 | 0.12 | 0.50 | 1.09 | 1.60 | 2.61 | 3.81 | 4.92 | 7.84 | 13.10 | 20.41 |
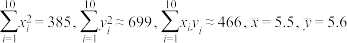 .
.(1)根据表中数据,求相关年份与全国新能源汽车保有量的样本相关系数(精确到0.01);
(2)现苏同学购买第1辆汽车时随机在新能源汽车和非新能源汽车中选择.如果第1辆购买新能源汽车,那么第2辆仍选择购买新能源汽车的概率为0.6;如果第1辆购买非新能源汽车,那么第2辆购买新能源汽车的概率为0.8,计算苏同学第2辆购买新能源汽车的概率;
(3)某汽车网站为调查新能源汽车车主的用车体验,决定从12名候选车主中选3名车主进行访谈,已知有4名候选车主是新能源汽车车主,假设每名候选人都有相同的机会被选到,求被选到新能源汽车车主的分布列及数学期望.
附:相关系数:
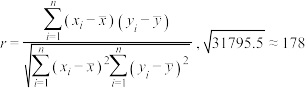 .
.
您最近一年使用:0次
昨日更新
|
205次组卷
|
2卷引用:重庆市开州中学2023-2024学年高三下学期高考模拟考试数学试题(四)
名校
6 . 对任意两个非零向量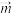 ,
, ,定义:
,定义:
(1)若向量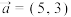 ,
, ,求
,求 的值;
的值;
(2)若单位向量 ,
, 满足
满足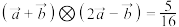 ,求向量
,求向量 与
与 的夹角的余弦值;
的夹角的余弦值;
(3)若非零向量 ,
, 满足
满足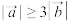 ,向量
,向量 与
与 的夹角是锐角,且
的夹角是锐角,且 是整数,求
是整数,求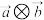 的取值范围.
的取值范围.
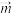 ,
, ,定义:
,定义:
(1)若向量
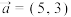 ,
, ,求
,求 的值;
的值;(2)若单位向量
 ,
, 满足
满足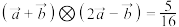 ,求向量
,求向量 与
与 的夹角的余弦值;
的夹角的余弦值;(3)若非零向量
 ,
, 满足
满足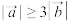 ,向量
,向量 与
与 的夹角是锐角,且
的夹角是锐角,且 是整数,求
是整数,求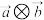 的取值范围.
的取值范围.
您最近一年使用:0次
名校
7 . 已知 为圆
为圆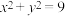 上一个动点,MN垂直
上一个动点,MN垂直 轴,垂足为N,O为坐标原点,
轴,垂足为N,O为坐标原点, 的重心为
的重心为 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)记(1)中的轨迹为曲线 ,直线
,直线 与曲线
与曲线 相交于A、B两点,点
相交于A、B两点,点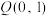 ,若点
,若点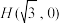 恰好是
恰好是 的垂心,求直线
的垂心,求直线 的方程.
的方程.
 为圆
为圆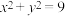 上一个动点,MN垂直
上一个动点,MN垂直 轴,垂足为N,O为坐标原点,
轴,垂足为N,O为坐标原点, 的重心为
的重心为 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)记(1)中的轨迹为曲线
 ,直线
,直线 与曲线
与曲线 相交于A、B两点,点
相交于A、B两点,点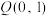 ,若点
,若点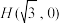 恰好是
恰好是 的垂心,求直线
的垂心,求直线 的方程.
的方程.
您最近一年使用:0次
名校
解题方法
8 . 已知函数 .
.
(1)当 时,
时,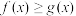 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)已知直线 是曲线
是曲线 的两条切线,且直线
的两条切线,且直线 的斜率之积为1.
的斜率之积为1.
(i)记 为直线
为直线 交点的横坐标,求证:
交点的横坐标,求证: ;
;
(ii)若 也与曲线
也与曲线 相切,求
相切,求 的关系式并求出
的关系式并求出 的取值范围.
的取值范围.
 .
.(1)当
 时,
时,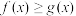 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)已知直线
 是曲线
是曲线 的两条切线,且直线
的两条切线,且直线 的斜率之积为1.
的斜率之积为1.(i)记
 为直线
为直线 交点的横坐标,求证:
交点的横坐标,求证: ;
;(ii)若
 也与曲线
也与曲线 相切,求
相切,求 的关系式并求出
的关系式并求出 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知 是二维离散型随机变量,其中X、Y是两个相互独立的离散型随机变量,
是二维离散型随机变量,其中X、Y是两个相互独立的离散型随机变量, 的分布列用表格表示如下:
的分布列用表格表示如下:
(1)求 和
和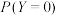 ;
;
(2)“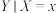 ”表示在
”表示在 条件下的
条件下的 的取值,求“
的取值,求“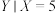 ”的分布列;
”的分布列;
(3) 为
为 的数学期望,
的数学期望,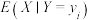 为“
为“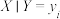 ”的分布的期望,证明:
”的分布的期望,证明: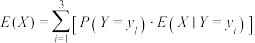 .
.
 是二维离散型随机变量,其中X、Y是两个相互独立的离散型随机变量,
是二维离散型随机变量,其中X、Y是两个相互独立的离散型随机变量, 的分布列用表格表示如下:
的分布列用表格表示如下:
X | 0 | 3 | 6 |
0 |
|
|
|
5 |
|
|
|
(1)求
 和
和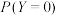 ;
;(2)“
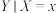 ”表示在
”表示在 条件下的
条件下的 的取值,求“
的取值,求“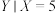 ”的分布列;
”的分布列;(3)
 为
为 的数学期望,
的数学期望,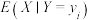 为“
为“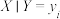 ”的分布的期望,证明:
”的分布的期望,证明: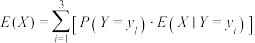 .
.
您最近一年使用:0次
名校
解题方法
10 . 定义空间中既有大小又有方向的量为空间向量.起点为 ,终点为
,终点为 的空间向量记作
的空间向量记作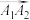 ,其大小称为
,其大小称为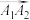 的模,记作
的模,记作 等于
等于 两点间的距离.模为零的向量称为零向量,记作
两点间的距离.模为零的向量称为零向量,记作 .空间向量的加法、减法以及数乘运算的定义与性质和平面向量一致,如:对任意空间向量
.空间向量的加法、减法以及数乘运算的定义与性质和平面向量一致,如:对任意空间向量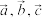 ,均有
,均有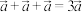
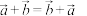 ,
,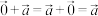 ,
,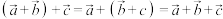 ;对任意实数
;对任意实数 和空间向量
和空间向量 ,均有
,均有 ;对任意三点
;对任意三点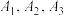 ,均有
,均有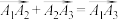 等.已知体积为
等.已知体积为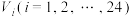 的三棱锥
的三棱锥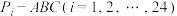 的底面均为
的底面均为 ,在
,在 中,
中,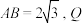 是
是 内一点,
内一点,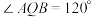 .记
.记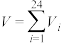 .
.
(1)若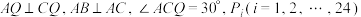 到平面
到平面 的距离均为1,求
的距离均为1,求 ;
;
(2)若 是
是 的重心,且对任意
的重心,且对任意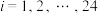 ,均有
,均有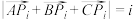 .
.
(i)求 的最大值;
的最大值;
(ii)当 最大时,5个分别由24个实数组成的24元数组
最大时,5个分别由24个实数组成的24元数组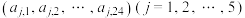 满足对任意
满足对任意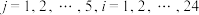 ,均有
,均有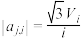 ,且对任意
,且对任意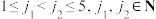 均有
均有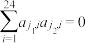 求证:
求证: 不可能对任意
不可能对任意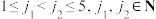 及
及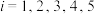 均成立.
均成立.
(参考公式: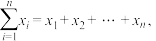
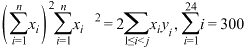 )
)
 ,终点为
,终点为 的空间向量记作
的空间向量记作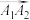 ,其大小称为
,其大小称为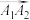 的模,记作
的模,记作 等于
等于 两点间的距离.模为零的向量称为零向量,记作
两点间的距离.模为零的向量称为零向量,记作 .空间向量的加法、减法以及数乘运算的定义与性质和平面向量一致,如:对任意空间向量
.空间向量的加法、减法以及数乘运算的定义与性质和平面向量一致,如:对任意空间向量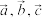 ,均有
,均有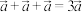
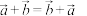 ,
,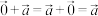 ,
,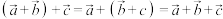 ;对任意实数
;对任意实数 和空间向量
和空间向量 ,均有
,均有 ;对任意三点
;对任意三点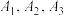 ,均有
,均有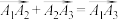 等.已知体积为
等.已知体积为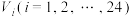 的三棱锥
的三棱锥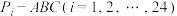 的底面均为
的底面均为 ,在
,在 中,
中,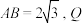 是
是 内一点,
内一点,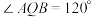 .记
.记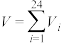 .
.(1)若
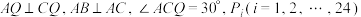 到平面
到平面 的距离均为1,求
的距离均为1,求 ;
;(2)若
 是
是 的重心,且对任意
的重心,且对任意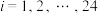 ,均有
,均有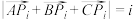 .
.(i)求
 的最大值;
的最大值;(ii)当
 最大时,5个分别由24个实数组成的24元数组
最大时,5个分别由24个实数组成的24元数组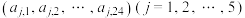 满足对任意
满足对任意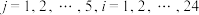 ,均有
,均有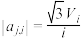 ,且对任意
,且对任意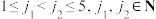 均有
均有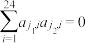 求证:
求证: 不可能对任意
不可能对任意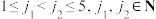 及
及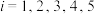 均成立.
均成立.(参考公式:
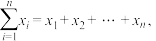
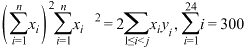 )
)
您最近一年使用:0次