解题方法
1 . 已知双曲线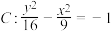 的焦点分别为
的焦点分别为 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )
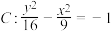 的焦点分别为
的焦点分别为 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )A.渐近线方程为 |
B.双曲线 与椭圆 与椭圆 的离心率互为倒数 的离心率互为倒数 |
C.若双曲线 上一点 上一点 满足 满足 ,则 ,则 的周长为34 的周长为34 |
D.若从双曲线 的左、右支上任取一点,则这两点的最短距离为6 的左、右支上任取一点,则这两点的最短距离为6 |
您最近一年使用:0次
2 . 某研发团队研究出了一种新型智能产品,经过调研发现该产品推出市场的时间 (单位:年)与市场占有率
(单位:年)与市场占有率 可近似用函数
可近似用函数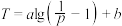 来描述,其中
来描述,其中 ,
, 是常数.已知该产品市场占有率为
是常数.已知该产品市场占有率为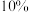 时,需要1年;市场占有率为
时,需要1年;市场占有率为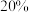 时,需要1.5年,则市场占有率达到
时,需要1.5年,则市场占有率达到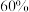 时约需( )(
时约需( )(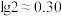 ,
, )
)
 (单位:年)与市场占有率
(单位:年)与市场占有率 可近似用函数
可近似用函数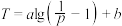 来描述,其中
来描述,其中 ,
, 是常数.已知该产品市场占有率为
是常数.已知该产品市场占有率为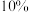 时,需要1年;市场占有率为
时,需要1年;市场占有率为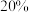 时,需要1.5年,则市场占有率达到
时,需要1.5年,则市场占有率达到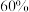 时约需( )(
时约需( )(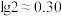 ,
, )
)| A.2.32年 | B.2.43年 | C.2.58年 | D.2.81年 |
您最近一年使用:0次
3 . 我国杂交水稻技术在世界上处于先进水平,某农场有甲、乙两块面积相同的稻田,种植同一品种杂交水稻,连续6年的产量如下,则下列说法正确的是( )
| 年份序号 | 1 | 2 | 3 | 4 | 5 | 6 |
甲稻田产量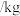 | 900 | 920 | 900 | 850 | 910 | 920 |
乙稻田产量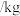 | 890 | 960 | 950 | 850 | 860 | 890 |
| A.甲、乙两块稻田的样本平均数相等 |
| B.将两组数据按从小到大的顺序排成一行,则中位数为900 |
| C.两组数据的方差相同 |
| D.甲组数据的标准差大于乙组数据的标准差 |
您最近一年使用:0次
4 . 在政府精准扶贫政策的扶持下,甲、乙,丙三位学徒跟老李师傅学习制作某种陶器,经过一段时间的学习后,他们各自能制作成功该陶器的概率分别为 ,
, ,
, ,且
,且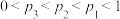 .现需要他们三人制作一件该陶器,每次只有一个人制作,且每个人只制作一次,如果有一个人制作失败则换下一个人重新制作,若陶器制作成功则结束.
.现需要他们三人制作一件该陶器,每次只有一个人制作,且每个人只制作一次,如果有一个人制作失败则换下一个人重新制作,若陶器制作成功则结束.
(1)按照甲、乙、丙的顺序制作该陶器,若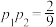 ,且
,且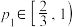 ,求制作该陶器的人数均值的最大值;
,求制作该陶器的人数均值的最大值;
(2)若这种陶器制作成功后需要两轮检测都合格才能上市销售,已知学徒甲制作的陶器第一轮检测合格的概率为 ,第二轮检测合格的概率为
,第二轮检测合格的概率为 ,且两轮检测是否合格相互之间没有影响.如果这种陶器可以上市销售,则每件陶器可获利100元;如果这种陶器不能上市销售,则每件陶器亏损80元.现有学徒甲制作的这种陶器4件,求这4件陶器获利220元的概率.
,且两轮检测是否合格相互之间没有影响.如果这种陶器可以上市销售,则每件陶器可获利100元;如果这种陶器不能上市销售,则每件陶器亏损80元.现有学徒甲制作的这种陶器4件,求这4件陶器获利220元的概率.
 ,
, ,
, ,且
,且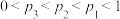 .现需要他们三人制作一件该陶器,每次只有一个人制作,且每个人只制作一次,如果有一个人制作失败则换下一个人重新制作,若陶器制作成功则结束.
.现需要他们三人制作一件该陶器,每次只有一个人制作,且每个人只制作一次,如果有一个人制作失败则换下一个人重新制作,若陶器制作成功则结束.(1)按照甲、乙、丙的顺序制作该陶器,若
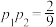 ,且
,且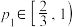 ,求制作该陶器的人数均值的最大值;
,求制作该陶器的人数均值的最大值;(2)若这种陶器制作成功后需要两轮检测都合格才能上市销售,已知学徒甲制作的陶器第一轮检测合格的概率为
 ,第二轮检测合格的概率为
,第二轮检测合格的概率为 ,且两轮检测是否合格相互之间没有影响.如果这种陶器可以上市销售,则每件陶器可获利100元;如果这种陶器不能上市销售,则每件陶器亏损80元.现有学徒甲制作的这种陶器4件,求这4件陶器获利220元的概率.
,且两轮检测是否合格相互之间没有影响.如果这种陶器可以上市销售,则每件陶器可获利100元;如果这种陶器不能上市销售,则每件陶器亏损80元.现有学徒甲制作的这种陶器4件,求这4件陶器获利220元的概率.
您最近一年使用:0次
5 . 如图是清代的时钟,以中国传统的一日十二个时辰为表盘显水,其内部结构与普通机械钟表的内部结构相似,内部表盘为圆形,外部环形装饰部分宽度为5厘米,此表挂在墙上,最高点距离地面的高度为2.35米,最低点距离地面的高度为1.95米,以子时为正向上方向,一官员去上早朝时,看到家中时钟的指针指向寅时(指针尖的轨迹为表盘边沿),若4个半时辰后回到家中,此时指针尖到地面的高度约为(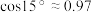 )( )
)( )

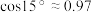 )( )
)( )
| A.199.1cm | B.201.1cm | C.200.5cm | D.218.9cm |
您最近一年使用:0次
6 . 有一组样本数据如下:
56,62,63,63,65,66,68,69,71,74,76,76,77,78,79,79,82,85,87,88,95,98
则其25%分位数、中位数与75%分位数分别为( )
56,62,63,63,65,66,68,69,71,74,76,76,77,78,79,79,82,85,87,88,95,98
则其25%分位数、中位数与75%分位数分别为( )
| A.65,76,82 | B.66,74,82 | C.66,76,79 | D.66,76,82 |
您最近一年使用:0次
2023-05-04更新
|
1246次组卷
|
7卷引用:海南省2022届高三高考全真模拟卷(四)数学试题
海南省2022届高三高考全真模拟卷(四)数学试题(已下线)9.2.2 总体百分位数的估计(已下线)期末模拟卷(A卷·基础通关卷)-【单元测试】湖南省长沙市明德中学2022-2023学年高一下学期5月月考数学试题(已下线)第05讲 统计与概率14种常见考法归类(2)广东湛江市2022-2023学年高二下学期期末数学试题云南省祥华教育集团2023-2024学年高一下学期5月联考数学试题
解题方法
7 . 新冠病毒在传播过程中会发生变异,现在已有多种变异毒株,传播能力和重症率都各不相同.某地卫生部门统计了本地新冠确诊病例中感染每种毒株的患者在总病例中的比例和各自的重症率,数据统计如下表所示.
已知当地将阿尔法、贝尔塔、德尔塔三种类型病例全部集中收治在甲医院,奥密克戎病例全部单独收治在乙医院.以频率估计概率回答下列问题.
(1)某医生从甲医院新冠确诊病例名单中任取1人,求其为重症病例的概率;
(2)某医生从乙医院新冠确诊病例名单中任取2人,已知2人中有重症病例,求2人都是重症病例的概率(结果保留4位小数).
| 病毒类型 | 在确诊病例中的比例 | 重症率 |
阿尔法 | 10% | 2.4% |
贝尔特 | 15% | 3.8% |
德尔塔 | 25% | 4% |
奥密克戎 | 50% | 2% |
(1)某医生从甲医院新冠确诊病例名单中任取1人,求其为重症病例的概率;
(2)某医生从乙医院新冠确诊病例名单中任取2人,已知2人中有重症病例,求2人都是重症病例的概率(结果保留4位小数).
您最近一年使用:0次
解题方法
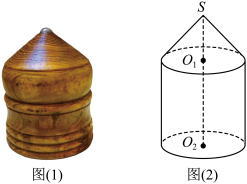
8 . 陀螺是中国民间最早的娱乐工具之一,起源于石器时代,它是绕一个支点高速转动的几何体,其上半部分为圆锥,下半部分为同底的圆柱.如图(1)为陀螺实物体,图(2)为陀螺的直观图.已知 ,
, 分别为圆柱两个底面圆心,设一个陀螺的外接球(圆柱上、下底面圆周与圆锥顶点均在球面上)的半径为
分别为圆柱两个底面圆心,设一个陀螺的外接球(圆柱上、下底面圆周与圆锥顶点均在球面上)的半径为 ,球心为
,球心为 ,点
,点 为圆锥顶点.若圆锥与圆柱的体积比为
为圆锥顶点.若圆锥与圆柱的体积比为 ,则圆柱的体积为
,则圆柱的体积为_________ .
 ,
, 分别为圆柱两个底面圆心,设一个陀螺的外接球(圆柱上、下底面圆周与圆锥顶点均在球面上)的半径为
分别为圆柱两个底面圆心,设一个陀螺的外接球(圆柱上、下底面圆周与圆锥顶点均在球面上)的半径为 ,球心为
,球心为 ,点
,点 为圆锥顶点.若圆锥与圆柱的体积比为
为圆锥顶点.若圆锥与圆柱的体积比为 ,则圆柱的体积为
,则圆柱的体积为
您最近一年使用:0次
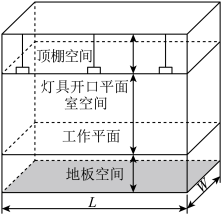
9 . 在建筑学中,照明设计通常要参考“顶棚空间比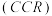 、室空间比
、室空间比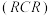 和地板空间比
和地板空间比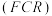 ”,因此通常将一个房间分为“顶棚空间、室空间和地板空间”,如图所示,其中室空间比的计算公式为:
”,因此通常将一个房间分为“顶棚空间、室空间和地板空间”,如图所示,其中室空间比的计算公式为: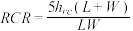 (
(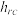 表示灯具开口平面至工作平面的高度,
表示灯具开口平面至工作平面的高度, ,
, 表示房间的长和宽),现有一教室尺寸(长
表示房间的长和宽),现有一教室尺寸(长 宽
宽 高)为
高)为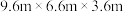 ,灯具开口平面离顶棚
,灯具开口平面离顶棚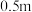 ,工作平面离地板平面
,工作平面离地板平面 ,则室空间比
,则室空间比 的值约为( )
的值约为( )
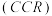 、室空间比
、室空间比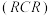 和地板空间比
和地板空间比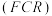 ”,因此通常将一个房间分为“顶棚空间、室空间和地板空间”,如图所示,其中室空间比的计算公式为:
”,因此通常将一个房间分为“顶棚空间、室空间和地板空间”,如图所示,其中室空间比的计算公式为: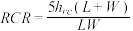 (
(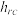 表示灯具开口平面至工作平面的高度,
表示灯具开口平面至工作平面的高度, ,
, 表示房间的长和宽),现有一教室尺寸(长
表示房间的长和宽),现有一教室尺寸(长 宽
宽 高)为
高)为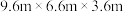 ,灯具开口平面离顶棚
,灯具开口平面离顶棚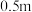 ,工作平面离地板平面
,工作平面离地板平面 ,则室空间比
,则室空间比 的值约为( )
的值约为( )
| A.2.64 | B.2.94 | C.3.16 | D.3.24 |
您最近一年使用:0次
解题方法
10 . 近年来青少年近视问题日趋严重,引起了政府、教育部门和社会各界的高度关切.一研究机构为了解近视与户外活动时间的关系,对某地区的小学生随机调查了100人,得到如下数据:
(1)从这些小学生中任选1人,A表示事件“该小学生近视”,B表示事件“该小学生平均每天户外活动时间不足1小时”,分别求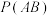 和
和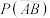 ;
;
(2)完成下面的列联表,根据小概率值 的独立性检验,能否认为近视与户外活动时间有关系?
的独立性检验,能否认为近视与户外活动时间有关系?
附:
| 平均每天户外活动时间 | 不足1小时 | 1小时以上,不足2小时 | 2小时以上 |
| 近视 | 15 | 8 | 2 |
| 不近视 | 15 | 32 | 28 |
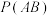 和
和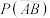 ;
;(2)完成下面的列联表,根据小概率值
 的独立性检验,能否认为近视与户外活动时间有关系?
的独立性检验,能否认为近视与户外活动时间有关系?| 平均每天户外活动时间 | 不足2小时 | 2小时以上 |
| 近视 | ||
| 不近视 |

 | 0.05 | 0.01 | 0.005 |
 | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次



