名校
解题方法
1 . 德国数学家黎曼(Ricmann)提出的黎曼函数r(x)在分析学中有着广泛的应用.黎曼函数r(x)的定义为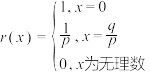 ,(p∈N*,q∈Z,q≠0且p,q互素),下列命题中,正确的有( )
,(p∈N*,q∈Z,q≠0且p,q互素),下列命题中,正确的有( )
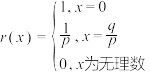 ,(p∈N*,q∈Z,q≠0且p,q互素),下列命题中,正确的有( )
,(p∈N*,q∈Z,q≠0且p,q互素),下列命题中,正确的有( )A.存在常数T > 0,使得对任意的x∈R,都有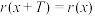 |
B.对任意的x∈R,有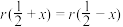 |
C.存在a,b,a + b∈[0,1],使得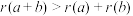 |
D.给定正整数t,记S =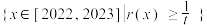 ,则S有 ,则S有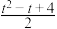 个元素 个元素 |
您最近一年使用:0次
2022-11-05更新
|
427次组卷
|
2卷引用:四川省四川外国语大学附属外国语学校2022-2023学年高一上学期期中数学试题
解题方法
2 . 下列各项说法正确的有( )
A. 可以表示y是x的函数 可以表示y是x的函数 | B.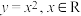 与 与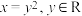 是相同函数 是相同函数 |
C.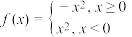 是奇函数 是奇函数 | D. 在定义域内是减函数 在定义域内是减函数 |
您最近一年使用:0次
名校
解题方法
3 . 若定义域是 的函数
的函数 满足:①
满足:① ,
, ,都有
,都有 ;②
;② ,
, ,且
,且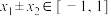 ,都有
,都有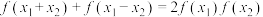 .则下列结论正确的是( )
.则下列结论正确的是( )
 的函数
的函数 满足:①
满足:① ,
, ,都有
,都有 ;②
;② ,
, ,且
,且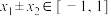 ,都有
,都有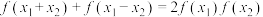 .则下列结论正确的是( )
.则下列结论正确的是( )A. | B.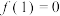 |
C.函数 是偶函数 是偶函数 | D. ,都有 ,都有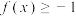 |
您最近一年使用:0次
2022-10-30更新
|
784次组卷
|
4卷引用:云南师范大学附属中学2022-2023学年高一上学期教学测评期中卷数学试题
名校
4 . 函数 满足
满足 ,
,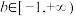 ,
, (a,b不同时为
(a,b不同时为 ),当
),当 时,
时,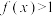 .若
.若 在集合
在集合 或
或 上是偶函数,数列
上是偶函数,数列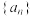 满足
满足 ,
,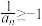 ,
,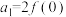 ,
, ,则( )
,则( )
 满足
满足 ,
,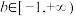 ,
, (a,b不同时为
(a,b不同时为 ),当
),当 时,
时,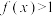 .若
.若 在集合
在集合 或
或 上是偶函数,数列
上是偶函数,数列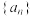 满足
满足 ,
,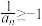 ,
,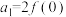 ,
, ,则( )
,则( )A. 在区间 在区间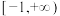 上单调递减 上单调递减 |
B.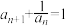 |
C.不等式 的解集为 的解集为 |
D. |
您最近一年使用:0次
名校
解题方法
5 . 下列命题中是真命题的是( )
A.“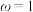 ”是“ ”是“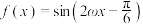 的最小正周期为 的最小正周期为 ”的必要不充分条件 ”的必要不充分条件 |
B.已知平面向量 , , 的夹角为 的夹角为 , , , ,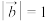 ,则 ,则 |
C.为了得到函数 的图象,只需把函数 的图象,只需把函数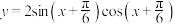 的图象向左平行移动 的图象向左平行移动 个单位长度 个单位长度 |
D.函数 是定义在 是定义在 上的偶函数且在 上的偶函数且在 上为减函数, 上为减函数, ,则不等式 ,则不等式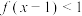 的解集为 的解集为 |
您最近一年使用:0次
2022-09-29更新
|
605次组卷
|
2卷引用:辽宁省本溪市本溪县高级中学2022-2023学年高三上学期第一次月考数学试题
名校
6 . 下列命题中正确的是( )
A.幂函数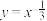 在 在 内是减函数 内是减函数 |
B.函数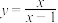 在区间 在区间 内是减函数 内是减函数 |
C.如果函数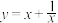 在 在 上是增函数,那么它在 上是增函数,那么它在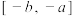 上是减函数 上是减函数 |
D.若定义在 上的函数 上的函数 的图象关于直线 的图象关于直线 对称,且 对称,且 在直线 在直线 的右侧单减,则函数 的右侧单减,则函数 在直线 在直线 的左侧单增 的左侧单增 |
您最近一年使用:0次
名校
解题方法
7 . 设函数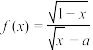 ,则下列说法正确的是( )
,则下列说法正确的是( )
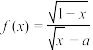 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若 ,则 ,则 在 在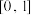 上单调递减 上单调递减 | B.若 , , 无最大值,也无最小值 无最大值,也无最小值 |
C.若 ,则 ,则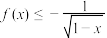 | D.若 ,则 ,则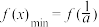 |
您最近一年使用:0次
2022-09-21更新
|
784次组卷
|
3卷引用:2022年浙江省温州市摇篮杯高一数学竞赛试题
名校
解题方法
8 . 已知函数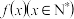 与
与 满足:①
满足:①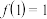 ,②
,② ,③
,③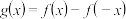 ,则下列结论正确的是( )
,则下列结论正确的是( )
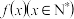 与
与 满足:①
满足:①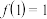 ,②
,② ,③
,③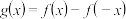 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 在定义域内单调递增 在定义域内单调递增 |
B.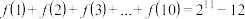 |
C. 在定义域内单调递减 在定义域内单调递减 |
D.当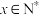 时,存在 时,存在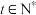 使得 使得 成立 成立 |
您最近一年使用:0次
2022-08-22更新
|
586次组卷
|
2卷引用:云南省昆明市第一中学高中新课标2023届高三第一次摸底测试数学试题
名校
9 . 已知  两点位于直线
两点位于直线  两侧,
两侧,  是直线
是直线  上两点, 且
上两点, 且  的面积是
的面积是  的面积的 2 倍,若
的面积的 2 倍,若 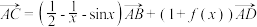 , 下列说法正确的是( )
, 下列说法正确的是( )
 两点位于直线
两点位于直线  两侧,
两侧,  是直线
是直线  上两点, 且
上两点, 且  的面积是
的面积是  的面积的 2 倍,若
的面积的 2 倍,若 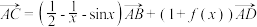 , 下列说法正确的是( )
, 下列说法正确的是( )A. 为奇函数 为奇函数 |
B. 在 在 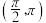 单调递减 单调递减 |
C. 在 在  有且仅有两个零点 有且仅有两个零点 |
D. 是周期函数 是周期函数 |
您最近一年使用:0次
2022-07-21更新
|
1349次组卷
|
5卷引用:吉林省东北师范大学附属中学2021-2022学年高一下学期阶段性考试数学试题
名校
解题方法
10 . 设函数 ,且
,且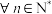 都有
都有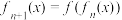 ,则下列判断正确的是( )
,则下列判断正确的是( )
 ,且
,且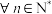 都有
都有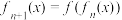 ,则下列判断正确的是( )
,则下列判断正确的是( )A.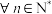 , , 的图象关于原点对称 的图象关于原点对称 |
B.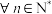 ,直线 ,直线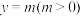 和 和 的图象至多只有一个交点 的图象至多只有一个交点 |
C.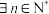 ,命题“ ,命题“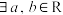 ,满足 ,满足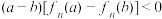 ”成立 ”成立 |
D.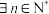 ,使得 ,使得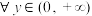 ,都有 ,都有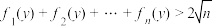 成立 成立 |
您最近一年使用:0次
2022-07-11更新
|
301次组卷
|
2卷引用:福建省漳州市四校2021-2022学年高二下学期期末联考数学试题



