解题方法
1 . 已知偶函数 在
在 上单调递增,
上单调递增,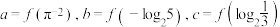 ,则( )
,则( )
 在
在 上单调递增,
上单调递增,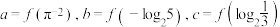 ,则( )
,则( )A.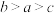 | B. |
C.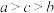 | D.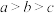 |
您最近一年使用:0次
名校
解题方法
2 . 设函数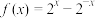 ,则使得
,则使得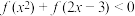 成立的
成立的 的
的解集 是____________ .
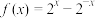 ,则使得
,则使得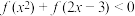 成立的
成立的 的
的
您最近一年使用:0次
2024-10-14更新
|
1995次组卷
|
4卷引用:江苏省前黄高级中学2024-2025学年高三上学期期初检测数学试题
3 . 设函数 若
若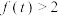 ,则
,则 的取值范围是( )
的取值范围是( )
 若
若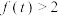 ,则
,则 的取值范围是( )
的取值范围是( )A. | B. |
C.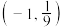 | D.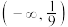 |
您最近一年使用:0次
名校
4 . 以下函数满足 的是( )
的是( )
 的是( )
的是( )A.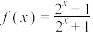 | B. |
C.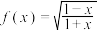 | D.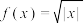 |
您最近一年使用:0次
2024-10-12更新
|
289次组卷
|
3卷引用:广东省部分学校大联考2022-2023学年高三下学期模拟(二)数学试题
名校
5 . 函数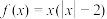 在
在 上的最小值为
上的最小值为 ,最大值为1,则
,最大值为1,则 的最大值为
的最大值为______ .
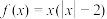 在
在 上的最小值为
上的最小值为 ,最大值为1,则
,最大值为1,则 的最大值为
的最大值为
您最近一年使用:0次
名校
6 . 定义在R上的奇函数 满足:任意
满足:任意 ,都有
,都有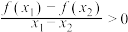 ,设
,设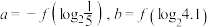 ,
,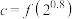 ,则
,则 的大小关系为( )
的大小关系为( )
 满足:任意
满足:任意 ,都有
,都有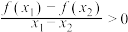 ,设
,设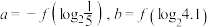 ,
,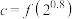 ,则
,则 的大小关系为( )
的大小关系为( )A.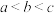 | B.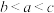 | C.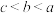 | D. |
您最近一年使用:0次
2024-10-12更新
|
1047次组卷
|
6卷引用:山西省大同市阳高县第一中学2022-2023学年高一上学期期末数学试题
名校
解题方法
7 . 已知定义在R的偶函数 对任意的x满足
对任意的x满足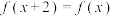 ,当
,当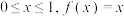 ,函数
,函数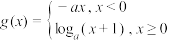 ,(
,( 且
且 ),则下列结论正确的有( )
),则下列结论正确的有( )
 对任意的x满足
对任意的x满足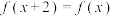 ,当
,当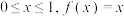 ,函数
,函数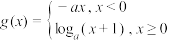 ,(
,( 且
且 ),则下列结论正确的有( )
),则下列结论正确的有( )A.函数 图象关于直线 图象关于直线 对称 对称 |
B.当 时, 时, |
C.若 在R上单调递减,则 在R上单调递减,则 |
D.若方程 在R上有4个不同的实数根,则实数a的取值范围是 在R上有4个不同的实数根,则实数a的取值范围是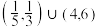 |
您最近一年使用:0次
名校
解题方法
8 . 已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,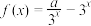 ,且
,且 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在正实数m,n,使得当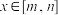 时,函数
时,函数 的值域为
的值域为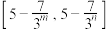 .若存在,求出m,n的值;若不存在,请说明理由.
.若存在,求出m,n的值;若不存在,请说明理由.
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,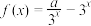 ,且
,且 .
.(1)求函数
 的解析式;
的解析式;(2)是否存在正实数m,n,使得当
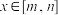 时,函数
时,函数 的值域为
的值域为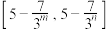 .若存在,求出m,n的值;若不存在,请说明理由.
.若存在,求出m,n的值;若不存在,请说明理由.
您最近一年使用:0次
解题方法
9 . 已知函数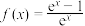 .
.
(1)求函数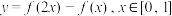 的值域;
的值域;
(2)若不等式 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;
(3)当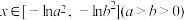 时,函数
时,函数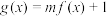 的值域为
的值域为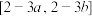 ,求正数
,求正数 的取值范围.
的取值范围.
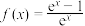 .
.(1)求函数
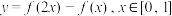 的值域;
的值域;(2)若不等式
 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围;(3)当
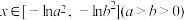 时,函数
时,函数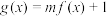 的值域为
的值域为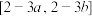 ,求正数
,求正数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-10-10更新
|
327次组卷
|
2卷引用:九师联盟2025届高三上学期10月联考数学试卷
名校
解题方法
10 . 设 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.
(1)求函数 在
在 上的解析式;
上的解析式;
(2)解关于 的不等式
的不等式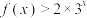 .
.
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.(1)求函数
 在
在 上的解析式;
上的解析式;(2)解关于
 的不等式
的不等式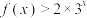 .
.
您最近一年使用:0次
2024-10-09更新
|
426次组卷
|
3卷引用:河北省保定市2022-2023学年高一上学期期末调研考试数学试题
河北省保定市2022-2023学年高一上学期期末调研考试数学试题(已下线)专题2 函数解析式与值域的求法【讲】(高一期中压轴专项)解答题广东省深圳市高级中学2024-2025学年高三上学期第一次诊断测试数学试题



