名校
解题方法
1 . 现定义“ 维形态复数
维形态复数 ”:
”: ,其中
,其中 为虚数单位,
为虚数单位, ,
, .
.
(1)当 时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
(2)若“2维形态复数”与“3维形态复数”相等,求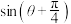 的值;
的值;
(3)若正整数 ,
,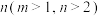 ,满足
,满足 ,
, ,证明:存在有理数
,证明:存在有理数 ,使得
,使得 .
.
 维形态复数
维形态复数 ”:
”: ,其中
,其中 为虚数单位,
为虚数单位, ,
, .
.(1)当
 时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;
时,证明:“2维形态复数”与“1维形态复数”之间存在平方关系;(2)若“2维形态复数”与“3维形态复数”相等,求
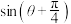 的值;
的值;(3)若正整数
 ,
,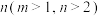 ,满足
,满足 ,
, ,证明:存在有理数
,证明:存在有理数 ,使得
,使得 .
.
您最近一年使用:0次
名校
2 . 在复平面内复数 ,
,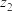 所对应的点为
所对应的点为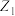 ,
,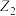 ,
, 为坐标原点,
为坐标原点, 是虚数单位.
是虚数单位.
(1) ,
,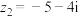 ,计算
,计算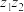 与
与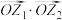 ;
;
(2)设 ,
,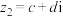
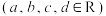 ,求证:
,求证: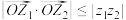 ,并指出向量
,并指出向量 ,
,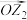 满足什么条件时该不等式取等号.
满足什么条件时该不等式取等号.
 ,
,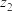 所对应的点为
所对应的点为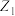 ,
,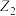 ,
, 为坐标原点,
为坐标原点, 是虚数单位.
是虚数单位.(1)
 ,
,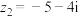 ,计算
,计算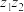 与
与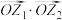 ;
;(2)设
 ,
,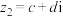
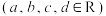 ,求证:
,求证: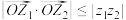 ,并指出向量
,并指出向量 ,
,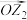 满足什么条件时该不等式取等号.
满足什么条件时该不等式取等号.
您最近一年使用:0次
3 . 我们把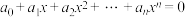 (其中
(其中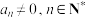 )称为一元
)称为一元 次多项式方程.代数基本定理:任何一元
次多项式方程.代数基本定理:任何一元 次复系数多项式方程(即
次复系数多项式方程(即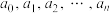 为实数)在复数集内至少有一个复数根;由此推得,任何一元
为实数)在复数集内至少有一个复数根;由此推得,任何一元 次复系数多项式方程在复数集内有且仅有
次复系数多项式方程在复数集内有且仅有 个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元
个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元 次复系数多项式在复数集内一定可以分解因式,转化为
次复系数多项式在复数集内一定可以分解因式,转化为 个一元一次多项式的积.即
个一元一次多项式的积.即 ,其中
,其中 ,
, 为方程
为方程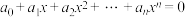 的根.进一步可以推出:在实系数范围内(即
的根.进一步可以推出:在实系数范围内(即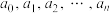 为实数),方程
为实数),方程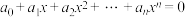 有实数根,则多项式
有实数根,则多项式 必可分解因式.例如:观察可知,
必可分解因式.例如:观察可知, 是方程
是方程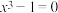 的一个根,则
的一个根,则 一定是多项式
一定是多项式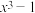 的一个因式,即
的一个因式,即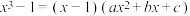 ,由待定系数法可知,
,由待定系数法可知, .
.
(1)在复数集内解方程: ;
;
(2)设 ,其中
,其中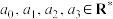 ,且
,且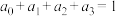 .
.
(i)分解因式: ;
;
(ii)记点 是
是 的图象与直线
的图象与直线 在第一象限内离原点最近的交点.求证:当
在第一象限内离原点最近的交点.求证:当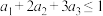 时,
时,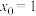 .
.
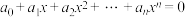 (其中
(其中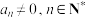 )称为一元
)称为一元 次多项式方程.代数基本定理:任何一元
次多项式方程.代数基本定理:任何一元 次复系数多项式方程(即
次复系数多项式方程(即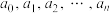 为实数)在复数集内至少有一个复数根;由此推得,任何一元
为实数)在复数集内至少有一个复数根;由此推得,任何一元 次复系数多项式方程在复数集内有且仅有
次复系数多项式方程在复数集内有且仅有 个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元
个复数根(重根按重数计算).那么我们由代数基本定理可知:任何一元 次复系数多项式在复数集内一定可以分解因式,转化为
次复系数多项式在复数集内一定可以分解因式,转化为 个一元一次多项式的积.即
个一元一次多项式的积.即 ,其中
,其中 ,
, 为方程
为方程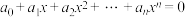 的根.进一步可以推出:在实系数范围内(即
的根.进一步可以推出:在实系数范围内(即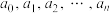 为实数),方程
为实数),方程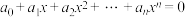 有实数根,则多项式
有实数根,则多项式 必可分解因式.例如:观察可知,
必可分解因式.例如:观察可知, 是方程
是方程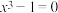 的一个根,则
的一个根,则 一定是多项式
一定是多项式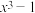 的一个因式,即
的一个因式,即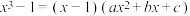 ,由待定系数法可知,
,由待定系数法可知, .
.(1)在复数集内解方程:
 ;
;(2)设
 ,其中
,其中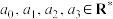 ,且
,且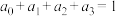 .
.(i)分解因式:
 ;
;(ii)记点
 是
是 的图象与直线
的图象与直线 在第一象限内离原点最近的交点.求证:当
在第一象限内离原点最近的交点.求证:当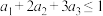 时,
时,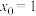 .
.
您最近一年使用:0次
2024高一下·全国·专题练习
4 . 求证:
(1)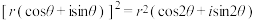 ;
;
(2) .
.
(1)
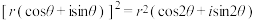 ;
;(2)
 .
.
您最近一年使用:0次
2024高一下·江苏·专题练习
5 . 设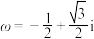 ,求证:
,求证:
(1)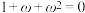 ;
;
(2)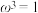 .
.
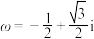 ,求证:
,求证:(1)
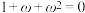 ;
;(2)
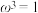 .
.
您最近一年使用:0次
名校
解题方法
6 . 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受.形如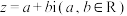 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当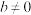 且时,
且时, 为纯虚数.其中
为纯虚数.其中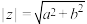 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,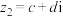 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成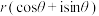 的形式,即
的形式,即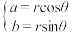 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定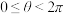 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.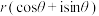 叫做复数
叫做复数 的三角形式.
的三角形式.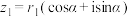 ,
,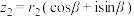 ,求
,求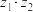 、
、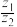 的三角形式;
的三角形式;
(2)设复数 ,
,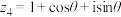 ,其中
,其中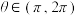 ,求
,求 ;
;
(3)在 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
① ;
;
②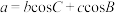 ,
,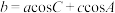 ,
,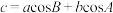 .
.
注意:使用复数以外的方法证明不给分.
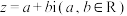 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当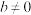 且时,
且时, 为纯虚数.其中
为纯虚数.其中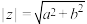 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,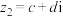 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成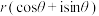 的形式,即
的形式,即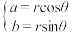 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定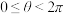 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.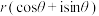 叫做复数
叫做复数 的三角形式.
的三角形式.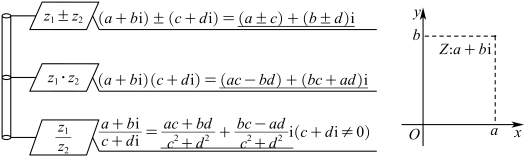
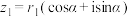 ,
,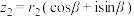 ,求
,求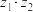 、
、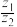 的三角形式;
的三角形式;(2)设复数
 ,
,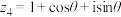 ,其中
,其中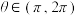 ,求
,求 ;
;(3)在
 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:①
 ;
;②
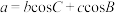 ,
,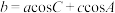 ,
,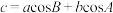 .
.注意:使用复数以外的方法证明不给分.
您最近一年使用:0次
2024-03-12更新
|
523次组卷
|
3卷引用:黑龙江省哈尔滨师范大学附属中学2023-2024学年高一下学期开学考试数学试卷
7 . 对于非空集合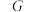 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在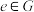 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得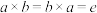 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意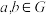 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群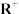 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群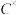 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
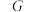 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
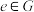 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得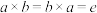 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意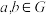 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
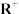 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群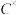 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近一年使用:0次
解题方法
8 . 设M是由复数组成的集合,对M的一个子集A,若存在复平面上的一个圆,使得A的所有数在复平面上对应的点都在圆内或圆周上,且 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
(1)判断 是否是
是否是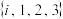 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;
(2)设复数z满足 ,其中
,其中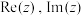 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: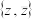 是
是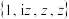 的“可分离子集”当且仅当
的“可分离子集”当且仅当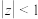 .
.
 中的数对应的点都在圆外,则称A是一个M的“可分离子集”.
中的数对应的点都在圆外,则称A是一个M的“可分离子集”.(1)判断
 是否是
是否是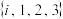 的“可分离子集”,并说明理由;
的“可分离子集”,并说明理由;(2)设复数z满足
 ,其中
,其中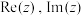 分别表示z的实部和虚部.证明:
分别表示z的实部和虚部.证明: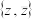 是
是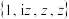 的“可分离子集”当且仅当
的“可分离子集”当且仅当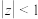 .
.
您最近一年使用:0次
2024高三·全国·专题练习
9 . 设 ,
,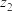 ,
, ,
, ,
, 为
为 个复数.
个复数.
(1)如果 ,求证:
,求证: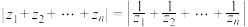 ;
;
(2)若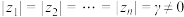 ,则有什么样的结果?
,则有什么样的结果?
 ,
,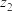 ,
, ,
, ,
, 为
为 个复数.
个复数.(1)如果
 ,求证:
,求证: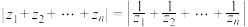 ;
;(2)若
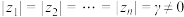 ,则有什么样的结果?
,则有什么样的结果?
您最近一年使用:0次
2024高三上·全国·专题练习
10 . 设 是虚数,
是虚数,
(1)求证 为实数的充要条件为
为实数的充要条件为 ;
;
(2)若 ,推测
,推测 为实数的充要条件;
为实数的充要条件;
(3)由上结论,求满足条件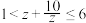 ,及实部与虚部均为整数的复数
,及实部与虚部均为整数的复数 .
.
 是虚数,
是虚数,(1)求证
 为实数的充要条件为
为实数的充要条件为 ;
;(2)若
 ,推测
,推测 为实数的充要条件;
为实数的充要条件;(3)由上结论,求满足条件
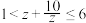 ,及实部与虚部均为整数的复数
,及实部与虚部均为整数的复数 .
.
您最近一年使用:0次



