名校
解题方法
1 . 对于正实数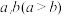 有基本不等式:
有基本不等式: ,其中
,其中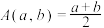 ,为
,为 的算术平均数,
的算术平均数,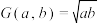 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设 ,求证:
,求证: :
:
(2)①证明不等式: :
:
②若不等式 对于任意的正实数
对于任意的正实数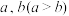 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
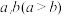 有基本不等式:
有基本不等式: ,其中
,其中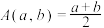 ,为
,为 的算术平均数,
的算术平均数,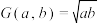 ,为
,为 的几何平均数.现定义
的几何平均数.现定义 的对数平均数:
的对数平均数:
(1)设
 ,求证:
,求证: :
:(2)①证明不等式:
 :
:②若不等式
 对于任意的正实数
对于任意的正实数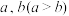 恒成立,求正实数
恒成立,求正实数 的最大值.
的最大值.
您最近半年使用:0次
2022-05-11更新
|
466次组卷
|
6卷引用:浙江省宁波市十校2021-2022学年高三上学期期末联考数学试题
名校
2 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴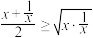 ,即
,即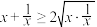 ,∴
,∴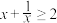 ,
,
当且仅当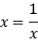 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值:
①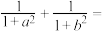 ___________.
___________.
②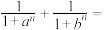 ___________.
___________.
(2)若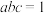 ,解方程
,解方程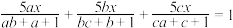 .
.
(3)若正数a、b满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴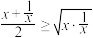 ,即
,即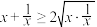 ,∴
,∴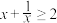 ,
,当且仅当
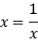 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值:①
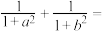 ___________.
___________.②
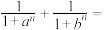 ___________.
___________.(2)若
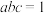 ,解方程
,解方程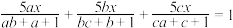 .
.(3)若正数a、b满足
 ,求
,求 的最小值.
的最小值.
您最近半年使用:0次
2021-10-29更新
|
512次组卷
|
3卷引用:江苏省南通中学2020-2021学年高一上学期开学考试数学试题
江苏省南通中学2020-2021学年高一上学期开学考试数学试题江西省南昌市第二中学2023-2024学年高一上学期月考数学试题(一)(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)
3 . 定义:函数 的导函数为
的导函数为 ,我们称函数
,我们称函数 的导函数
的导函数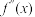 为函数
为函数 的二阶导函数.已知
的二阶导函数.已知 ,
,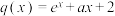 .
.
(1)求函数 的二阶导函数;
的二阶导函数;
(2)已知定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,
,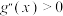 恒成立.
恒成立. 为曲线
为曲线 上的任意一点.求证:除点
上的任意一点.求证:除点 外,曲线
外,曲线 上每一点都在点
上每一点都在点 处切线的上方;
处切线的上方;
(3)试给出一个实数 的值,使得曲线
的值,使得曲线 与曲线
与曲线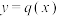 有且仅有一条公切线,并证明你的结论.
有且仅有一条公切线,并证明你的结论.
 的导函数为
的导函数为 ,我们称函数
,我们称函数 的导函数
的导函数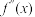 为函数
为函数 的二阶导函数.已知
的二阶导函数.已知 ,
,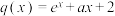 .
.(1)求函数
 的二阶导函数;
的二阶导函数;(2)已知定义在
 上的函数
上的函数 满足:对任意
满足:对任意 ,
,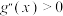 恒成立.
恒成立. 为曲线
为曲线 上的任意一点.求证:除点
上的任意一点.求证:除点 外,曲线
外,曲线 上每一点都在点
上每一点都在点 处切线的上方;
处切线的上方;(3)试给出一个实数
 的值,使得曲线
的值,使得曲线 与曲线
与曲线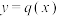 有且仅有一条公切线,并证明你的结论.
有且仅有一条公切线,并证明你的结论.
您最近半年使用:0次
4 . 现新定义两个复数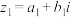 (
( 、
、 )和
)和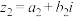 (
( 、
、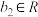 )之间的一个新运算
)之间的一个新运算 ,其运算法则为:
,其运算法则为: .
.
(1)请证明新运算 对于复数的加法满足分配律,即求证:
对于复数的加法满足分配律,即求证: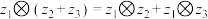 ;
;
(2)设运算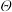 为运算
为运算 的逆运算,请推导运算
的逆运算,请推导运算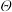 的运算法则.
的运算法则.
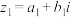 (
( 、
、 )和
)和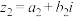 (
( 、
、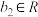 )之间的一个新运算
)之间的一个新运算 ,其运算法则为:
,其运算法则为: .
.(1)请证明新运算
 对于复数的加法满足分配律,即求证:
对于复数的加法满足分配律,即求证: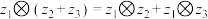 ;
;(2)设运算
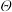 为运算
为运算 的逆运算,请推导运算
的逆运算,请推导运算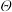 的运算法则.
的运算法则.
您最近半年使用:0次
2020-07-16更新
|
314次组卷
|
6卷引用:上海市静安区2019-2020学年高二下学期期末数学试题
上海市静安区2019-2020学年高二下学期期末数学试题(已下线)第三章 数系的扩充与复数的引入【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-2)沪教版(2020) 必修第二册 同步跟踪练习 第9章 复数 9.1~9.2 阶段综合训练苏教版(2019) 必修第二册 必杀技 专练1 新定义、新情境专练沪教版(2020) 必修第二册 同步跟踪练习 第9章 9.1~9.2阶段综合训练(已下线)7.2.2 复数的乘、除运算 (精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)
名校
5 . 已知函数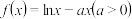 ,设
,设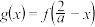 .
.
(1)判断函数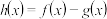 零点的个数,并给出证明;
零点的个数,并给出证明;
(2)首项为 的数列
的数列 满足:①
满足:①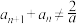 ;②
;② .其中
.其中 .求证:对于任意的
.求证:对于任意的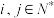 ,均有
,均有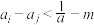 .
.
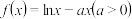 ,设
,设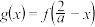 .
.(1)判断函数
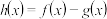 零点的个数,并给出证明;
零点的个数,并给出证明;(2)首项为
 的数列
的数列 满足:①
满足:①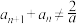 ;②
;② .其中
.其中 .求证:对于任意的
.求证:对于任意的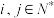 ,均有
,均有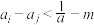 .
.
您最近半年使用:0次
2017-06-06更新
|
1718次组卷
|
3卷引用:湖南省长沙市雅礼中学2017届高考模拟试卷(二)数学(理)试题
名校
6 . 定义:若函数 图象上恰好存在相异的两点
图象上恰好存在相异的两点 满足曲线
满足曲线 在
在 和
和 处的切线重合,则称
处的切线重合,则称 为曲线
为曲线 的“双重切点”,直线
的“双重切点”,直线 为曲线
为曲线 的“双重切线”.
的“双重切线”.
(1)直线 是否为曲线
是否为曲线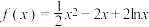 的“双重切线”,请说明理由;
的“双重切线”,请说明理由;
(2)已知函数 求曲线
求曲线 的“双重切线”的方程;
的“双重切线”的方程;
(3)已知函数 ,直线
,直线 为曲线
为曲线 的“双重切线”,记直线
的“双重切线”,记直线 的斜率所有可能的取值为
的斜率所有可能的取值为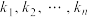 ,若
,若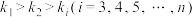 ,证明:
,证明: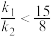 .
.
 图象上恰好存在相异的两点
图象上恰好存在相异的两点 满足曲线
满足曲线 在
在 和
和 处的切线重合,则称
处的切线重合,则称 为曲线
为曲线 的“双重切点”,直线
的“双重切点”,直线 为曲线
为曲线 的“双重切线”.
的“双重切线”.(1)直线
 是否为曲线
是否为曲线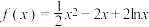 的“双重切线”,请说明理由;
的“双重切线”,请说明理由;(2)已知函数
 求曲线
求曲线 的“双重切线”的方程;
的“双重切线”的方程;(3)已知函数
 ,直线
,直线 为曲线
为曲线 的“双重切线”,记直线
的“双重切线”,记直线 的斜率所有可能的取值为
的斜率所有可能的取值为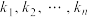 ,若
,若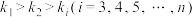 ,证明:
,证明: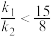 .
.
您最近半年使用:0次
2024-04-21更新
|
507次组卷
|
2卷引用:广西2024届高三4月模拟考试数学试卷
7 . 已知无穷数列 是首项为1,各项均为正整数的递增数列,集合
是首项为1,各项均为正整数的递增数列,集合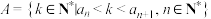 .若对于集合A中的元素k,数列
.若对于集合A中的元素k,数列 中存在不相同的项
中存在不相同的项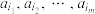 ,使得
,使得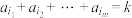 ,则称数列
,则称数列 具有性质
具有性质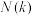 ,记集合
,记集合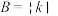 数列
数列 具有性质
具有性质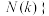 .
.
(1)若数列 的通项公式为
的通项公式为 写出集合A与集合B;
写出集合A与集合B;
(2)若集合A与集合B都是非空集合,且集合A中的最小元素为t,集合B中的最小元素为s,当 时,证明:
时,证明: ;
;
(3)若 满足
满足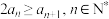 ,证明:
,证明: .
.
 是首项为1,各项均为正整数的递增数列,集合
是首项为1,各项均为正整数的递增数列,集合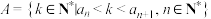 .若对于集合A中的元素k,数列
.若对于集合A中的元素k,数列 中存在不相同的项
中存在不相同的项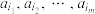 ,使得
,使得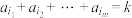 ,则称数列
,则称数列 具有性质
具有性质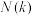 ,记集合
,记集合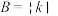 数列
数列 具有性质
具有性质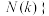 .
.(1)若数列
 的通项公式为
的通项公式为 写出集合A与集合B;
写出集合A与集合B;(2)若集合A与集合B都是非空集合,且集合A中的最小元素为t,集合B中的最小元素为s,当
 时,证明:
时,证明: ;
;(3)若
 满足
满足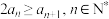 ,证明:
,证明: .
.
您最近半年使用:0次
8 . 对于非空集合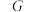 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:
1.(封闭性)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
2.(结合律)对于规定的“×”运算,对任意 ,都须满足
,都须满足 ;
;
3.(恒等元)存在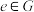 ,使得对任意
,使得对任意 ,
, ;
;
4.(逆的存在性)对任意 ,都存在
,都存在 ,使得
,使得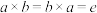 .
.
记群 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意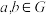 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).
(1)证明:所有实数在普通加法运算下构成群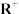 ;
;
(2)记 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群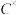 ,并说明理由;
,并说明理由;
(3)所有阶数小于等于四的群 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
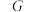 ,定义其在某一运算(统称乘法)“×”下的代数结构称为“群”
,定义其在某一运算(统称乘法)“×”下的代数结构称为“群” ,简记为
,简记为 .而判断
.而判断 是否为一个群,需验证以下三点:
是否为一个群,需验证以下三点:1.(封闭性)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;2.(结合律)对于规定的“×”运算,对任意
 ,都须满足
,都须满足 ;
;3.(恒等元)存在
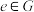 ,使得对任意
,使得对任意 ,
, ;
;4.(逆的存在性)对任意
 ,都存在
,都存在 ,使得
,使得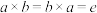 .
.记群
 所含的元素个数为
所含的元素个数为 ,则群
,则群 也称作“
也称作“ 阶群”.若群
阶群”.若群 的“×”运算满足交换律,即对任意
的“×”运算满足交换律,即对任意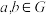 ,
, ,我们称
,我们称 为一个阿贝尔群(或交换群).
为一个阿贝尔群(或交换群).(1)证明:所有实数在普通加法运算下构成群
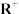 ;
;(2)记
 为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得
为所有模长为1的复数构成的集合,请找出一个合适的“×”运算使得 在该运算下构成一个群
在该运算下构成一个群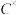 ,并说明理由;
,并说明理由;(3)所有阶数小于等于四的群
 是否都是阿贝尔群?请说明理由.
是否都是阿贝尔群?请说明理由.
您最近半年使用:0次
名校
解题方法
9 . 英国数学家泰勒发现了如下公式: 其中
其中 为自然对数的底数,
为自然对数的底数,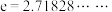 .以上公式称为泰勒公式.设
.以上公式称为泰勒公式.设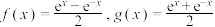 ,根据以上信息,并结合高中所学的数学知识,解决如下问题.
,根据以上信息,并结合高中所学的数学知识,解决如下问题.
(1)证明: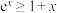 ;
;
(2)设 ,证明:
,证明: ;
;
(3)设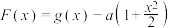 ,若
,若 是
是 的极小值点,求实数
的极小值点,求实数 的取值范围.
的取值范围.
 其中
其中 为自然对数的底数,
为自然对数的底数,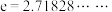 .以上公式称为泰勒公式.设
.以上公式称为泰勒公式.设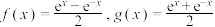 ,根据以上信息,并结合高中所学的数学知识,解决如下问题.
,根据以上信息,并结合高中所学的数学知识,解决如下问题.(1)证明:
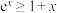 ;
;(2)设
 ,证明:
,证明: ;
;(3)设
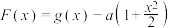 ,若
,若 是
是 的极小值点,求实数
的极小值点,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2024-03-03更新
|
1744次组卷
|
11卷引用:贵州省贵阳市2024届高三下学期适应性考试数学试卷(一)
贵州省贵阳市2024届高三下学期适应性考试数学试卷(一)贵州省安顺市2024届高三下学期模拟考试(一)数学试卷云南省玉溪市第一中学2023-2024学年高二下学期3月月考数学试题海南省海南华侨中学2023-2024学年高三下学期第二次模拟考试数学试题重庆市礼嘉中学2023-2024学年高二下学期第一次月考数学试题吉林省通化市梅河口市第五中学2023-2024学年高二下学期第一次月考数学试题重庆第十一中学校2023-2024学年高二下学期3月月考数学试题重庆市璧山中学校2023-2024学年高二下学期第一次月考数学试题广东省东莞市光明中学2023-2024学年高二下学期第一次月考数学试题四川省达州外国语学校2023-2024学年高二下学期3月月考数学试题黑龙江省哈尔滨市双城区兆麟中学2023-2024学年高二下学期第一次月考(4月)数学试题
名校
解题方法
10 . 给出下列两个定义:
I.对于函数 ,定义域为
,定义域为 ,且其在
,且其在 上是可导的,若其导函数定义域也为
上是可导的,若其导函数定义域也为 ,则称该函数是“同定义函数”.
,则称该函数是“同定义函数”.
II.对于一个“同定义函数” ,若有以下性质:
,若有以下性质:
①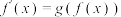 ;②
;②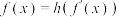 ,其中
,其中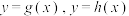 为两个新的函数,
为两个新的函数, 是
是 的导函数.
的导函数.
我们将具有其中一个性质的函数 称之为“单向导函数”,将两个性质都具有的函数
称之为“单向导函数”,将两个性质都具有的函数 称之为“双向导函数”,将
称之为“双向导函数”,将 称之为“自导函数”.
称之为“自导函数”.
(1)判断函数 和
和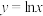 是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
(2)已知命题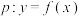 是“双向导函数”且其“自导函数”为常值函数,命题
是“双向导函数”且其“自导函数”为常值函数,命题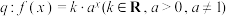 .判断命题
.判断命题 是
是 的什么条件,证明你的结论;
的什么条件,证明你的结论;
(3)已知函数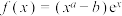 .
.
①若 的“自导函数”是
的“自导函数”是 ,试求
,试求 的取值范围;
的取值范围;
②若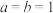 ,且定义
,且定义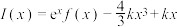 ,若对任意
,若对任意 ,不等式
,不等式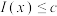 恒成立,求
恒成立,求 的取值范围.
的取值范围.
I.对于函数
 ,定义域为
,定义域为 ,且其在
,且其在 上是可导的,若其导函数定义域也为
上是可导的,若其导函数定义域也为 ,则称该函数是“同定义函数”.
,则称该函数是“同定义函数”.II.对于一个“同定义函数”
 ,若有以下性质:
,若有以下性质:①
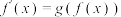 ;②
;②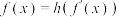 ,其中
,其中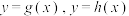 为两个新的函数,
为两个新的函数, 是
是 的导函数.
的导函数.我们将具有其中一个性质的函数
 称之为“单向导函数”,将两个性质都具有的函数
称之为“单向导函数”,将两个性质都具有的函数 称之为“双向导函数”,将
称之为“双向导函数”,将 称之为“自导函数”.
称之为“自导函数”.(1)判断函数
 和
和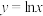 是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;
是“单向导函数”,或者“双向导函数”,说明理由.如果具有性质①,则写出其对应的“自导函数”;(2)已知命题
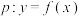 是“双向导函数”且其“自导函数”为常值函数,命题
是“双向导函数”且其“自导函数”为常值函数,命题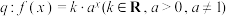 .判断命题
.判断命题 是
是 的什么条件,证明你的结论;
的什么条件,证明你的结论;(3)已知函数
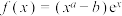 .
.①若
 的“自导函数”是
的“自导函数”是 ,试求
,试求 的取值范围;
的取值范围;②若
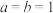 ,且定义
,且定义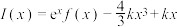 ,若对任意
,若对任意 ,不等式
,不等式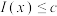 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近半年使用:0次
2024-02-20更新
|
2120次组卷
|
10卷引用:上海市普陀区桃浦中学2022-2023学年高二上学期12月月考数学试题
上海市普陀区桃浦中学2022-2023学年高二上学期12月月考数学试题上海市普陀区桃浦中学2022-2023学年高二上学期10月月考数学试题湖南省长沙市雅礼中学2024届高三月考试卷数学(六)浙江省湖州市第二中学2024届高三下学期新高考模拟数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编2024届高三新改革适应性模拟测试数学试卷四(九省联考题型)辽宁省沈阳市东北育才学校科学高中部2023-2024学年高三下学期第六次模拟考试数学试卷(已下线)上海市奉贤区2024届高三一模数学试题变式题16-21湖北省武昌实验中学2023-2024学年高二下学期三月月考数学试卷



