名校
解题方法
1 . 已知函数 ,
, ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)证明: 时,
时,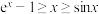 ;
;
(2)求函数 在
在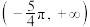 内的零点个数;
内的零点个数;
(3)若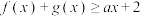 ,求
,求 的取值范围.
的取值范围.
 ,
, ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)证明:
 时,
时,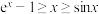 ;
;(2)求函数
 在
在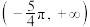 内的零点个数;
内的零点个数;(3)若
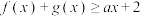 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2 . 如图,已知双曲线 的离心率为2,点
的离心率为2,点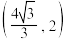 在C上,A,B为双曲线的左、右顶点,
在C上,A,B为双曲线的左、右顶点, 为右支上的动点,直线AP和直线x=1交于点N,直线NB交C的右支于点Q.
为右支上的动点,直线AP和直线x=1交于点N,直线NB交C的右支于点Q.
(2)探究直线PQ是否过定点,若过定点,求出该定点坐标,请说明理由;
(3)设S1,S2分别为△ABN和△NPQ的外接圆面积,求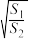 的取值范围.
的取值范围.
 的离心率为2,点
的离心率为2,点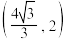 在C上,A,B为双曲线的左、右顶点,
在C上,A,B为双曲线的左、右顶点, 为右支上的动点,直线AP和直线x=1交于点N,直线NB交C的右支于点Q.
为右支上的动点,直线AP和直线x=1交于点N,直线NB交C的右支于点Q.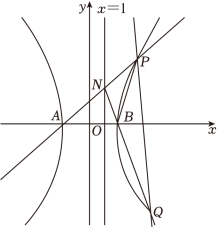
(2)探究直线PQ是否过定点,若过定点,求出该定点坐标,请说明理由;
(3)设S1,S2分别为△ABN和△NPQ的外接圆面积,求
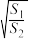 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-20更新
|
332次组卷
|
6卷引用:福建省福州市八县市一中2024届高三模拟预测数学试题
福建省福州市八县市一中2024届高三模拟预测数学试题安徽省池州市第一中学2024届高三第一次模拟联合检测数学试题吉林市第一中学2024届高三高考适应性训练(二)数学试题2024届吉林省吉林市第一中学高三数学适应性试卷(二)(已下线)专题7 圆锥曲线硬解定理【讲】(已下线)2025年新高考数学一轮复习收官卷02
名校
解题方法
3 . 已知线段 是圆
是圆 的一条长为2的弦,则
的一条长为2的弦,则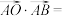 ( )
( )
 是圆
是圆 的一条长为2的弦,则
的一条长为2的弦,则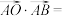 ( )
( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
名校
4 . 已知某种机器的电源电压U(单位:V)服从正态分布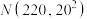 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
(1)求该机器生产的零件为不合格品时,电压不超过200V的概率;
(2)从该机器生产的零件中随机抽取n( )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.
附:若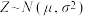 ,取
,取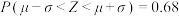 ,
,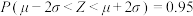 .
.
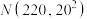 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.(1)求该机器生产的零件为不合格品时,电压不超过200V的概率;
(2)从该机器生产的零件中随机抽取n(
 )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.附:若
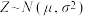 ,取
,取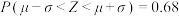 ,
,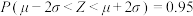 .
.
您最近一年使用:0次
2024-06-16更新
|
960次组卷
|
3卷引用:福建省福州市八县市一中2024届高三模拟预测数学试题
名校
解题方法
5 . 已知函数 在点
在点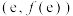 处的切线平行于直线
处的切线平行于直线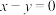 .
.
(1)若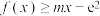 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)若 是函数
是函数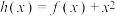 的极值点,求证:
的极值点,求证: .
.
 在点
在点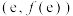 处的切线平行于直线
处的切线平行于直线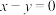 .
.(1)若
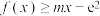 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)若
 是函数
是函数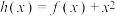 的极值点,求证:
的极值点,求证: .
.
您最近一年使用:0次
2024-06-16更新
|
711次组卷
|
2卷引用:福建省福州市八县市一中2024届高三模拟预测数学试题
名校
6 . 已知点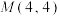 在抛物线
在抛物线 :
: (
( )上,
)上, 为
为 的焦点,则
的焦点,则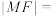 ( )
( )
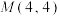 在抛物线
在抛物线 :
: (
( )上,
)上, 为
为 的焦点,则
的焦点,则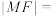 ( )
( )| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
7 . 将甲、乙等5名同学分配到3个社区进行志愿服务,要求每人只去一个社区,每个社区不能少于1人,且甲、乙在同一社区,则不同的安排方法数为( )
| A.54 | B.45 | C.36 | D.27 |
您最近一年使用:0次
8 . 在 中,角
中,角 所对应的边分别为
所对应的边分别为 ,点
,点 为边
为边 的中点,若
的中点,若 ,
,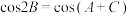 ,则
,则 ( )
( )
 中,角
中,角 所对应的边分别为
所对应的边分别为 ,点
,点 为边
为边 的中点,若
的中点,若 ,
,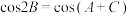 ,则
,则 ( )
( )A. | B. | C.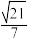 | D.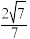 |
您最近一年使用:0次
名校
解题方法
9 . 如图,在四棱锥 中,
中,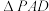 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,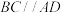 ,
, ,
, ,
, ,
, 分别为
分别为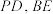 的中点.
的中点. 四点共面;
四点共面;
(2)求直线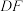 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,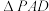 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,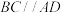 ,
, ,
, ,
, ,
, 分别为
分别为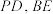 的中点.
的中点.
 四点共面;
四点共面;(2)求直线
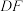 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
10 . 当药品 注射到人体内,它在血液中的残余量会以每小时
注射到人体内,它在血液中的残余量会以每小时 的速度减少,另一种药物
的速度减少,另一种药物 注射到人体内,它在血液中的残余量会以每小时
注射到人体内,它在血液中的残余量会以每小时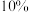 的速度减少.现同时给两位患者分别注射
的速度减少.现同时给两位患者分别注射 药品A和
药品A和 药品B,当两位患者体内药品的残余量恰好相等时,所经过的时间约为( )(参考数据:
药品B,当两位患者体内药品的残余量恰好相等时,所经过的时间约为( )(参考数据: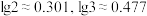 )
)
 注射到人体内,它在血液中的残余量会以每小时
注射到人体内,它在血液中的残余量会以每小时 的速度减少,另一种药物
的速度减少,另一种药物 注射到人体内,它在血液中的残余量会以每小时
注射到人体内,它在血液中的残余量会以每小时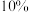 的速度减少.现同时给两位患者分别注射
的速度减少.现同时给两位患者分别注射 药品A和
药品A和 药品B,当两位患者体内药品的残余量恰好相等时,所经过的时间约为( )(参考数据:
药品B,当两位患者体内药品的残余量恰好相等时,所经过的时间约为( )(参考数据: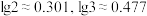 )
)A. | B.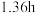 | C.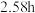 | D. |
您最近一年使用:0次



