名校
1 . 已知函数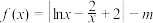 (
(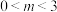 )有两个不同的零点
)有两个不同的零点 ,
, (
( ),下列关于
),下列关于 ,
, 的说法正确的有( )个
的说法正确的有( )个
①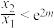 ②
② ③
③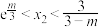 ④
④
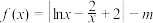 (
(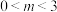 )有两个不同的零点
)有两个不同的零点 ,
, (
( ),下列关于
),下列关于 ,
, 的说法正确的有( )个
的说法正确的有( )个①
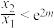 ②
② ③
③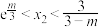 ④
④
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2024-01-08更新
|
809次组卷
|
8卷引用:江西省等七省联考2024届高三上学期最后一卷数学猜题卷(一)
江西省等七省联考2024届高三上学期最后一卷数学猜题卷(一)四川省南充市2024届高三一模数学(理)试题四川省南充市2024届高三一模数学(理)试题重庆市南开中学校2023-2024学年高二下学期阶段测试数学试题(已下线)思想02 运用数形结合的思想方法解题(4大题型)(练习)(已下线)【一题多变】函数零点问题(已下线)【一题多变】函数零点问题1(已下线)高二下学期第一次月考选择题压轴题十四大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
解题方法
2 . 定义域为 的函数
的函数 ,
, 的导函数分别为
的导函数分别为 ,
,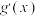 ,且
,且 ,
, ,则下列说法错误的为( )
,则下列说法错误的为( )
 的函数
的函数 ,
, 的导函数分别为
的导函数分别为 ,
,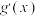 ,且
,且 ,
, ,则下列说法错误的为( )
,则下列说法错误的为( )A.当 是 是 的零点时, 的零点时, 是 是 的极大值点 的极大值点 |
B.当 是 是 的零点时, 的零点时, 是 是 的极小值点 的极小值点 |
C. , , 可能有相同的零点 可能有相同的零点 |
D. , , 可能有相同的极值点 可能有相同的极值点 |
您最近一年使用:0次
2024-01-07更新
|
251次组卷
|
2卷引用:江西省上饶市广丰贞白中学2024届高三上学期1月考试数学试题
名校
3 . 已知函数 .
.
(1)若 ,判断
,判断 在
在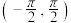 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)当 ,探究
,探究 在
在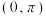 上的极值点个数.
上的极值点个数.
 .
.(1)若
 ,判断
,判断 在
在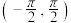 上的单调性,并说明理由;
上的单调性,并说明理由;(2)当
 ,探究
,探究 在
在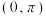 上的极值点个数.
上的极值点个数.
您最近一年使用:0次
2024-01-04更新
|
1632次组卷
|
8卷引用:江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(三)
江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(三)四川省遂宁市2024届高三一模数学(文)试题四川省广安市2024届高三一模数学(文)试题四川省雅安市2024届高三一模数学(文)试题四川省资阳市2024届高三二模数学(文)试题四川省眉山市2024届高三一模数学(文)试题(已下线)模块三 大招9 函数零点问题的处理大招(已下线)重难点06 导数必考压轴解答题全归类【十一大题型】
名校
4 . 已知函数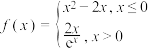 ,若关于
,若关于 的方程
的方程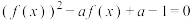 恰有四个不同的实数根,则实数
恰有四个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
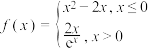 ,若关于
,若关于 的方程
的方程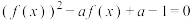 恰有四个不同的实数根,则实数
恰有四个不同的实数根,则实数 的取值范围是( )
的取值范围是( )A. | B.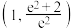 | C.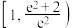 | D.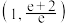 |
您最近一年使用:0次
7日内更新
|
466次组卷
|
9卷引用:江西省八所重点中学2022届高三4月联考数学(文)试题
23-24高三上·江西·阶段练习
名校
5 . 已知函数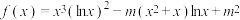 恰有4个零点,则
恰有4个零点,则 的取值范围是( )
的取值范围是( )
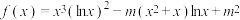 恰有4个零点,则
恰有4个零点,则 的取值范围是( )
的取值范围是( )A.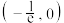 | B.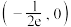 | C.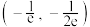 | D.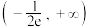 |
您最近一年使用:0次
2023-12-22更新
|
359次组卷
|
4卷引用:江西省“三新”协同教研共同体2024届高三上学期12月联考数学试题
(已下线)江西省“三新”协同教研共同体2024届高三上学期12月联考数学试题江西省部分学校2024届高三上学期12月联考数学试题广东省广州市执信中学2024届高三上学期元月阶段测试数学试题(已下线)微考点2-1 新高考新试卷结构中导数中零点根的个数问题(2大题型)
名校
6 . 已知函数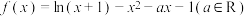 .
.
(1)当 时,存在
时,存在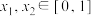 ,使得
,使得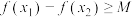 ,求M的最大值;
,求M的最大值;
(2)已知m,n是 的两个零点,记
的两个零点,记 为
为 的导函数,若
的导函数,若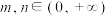 ,且
,且 ,证明:
,证明: .
.
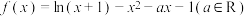 .
.(1)当
 时,存在
时,存在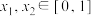 ,使得
,使得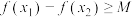 ,求M的最大值;
,求M的最大值;(2)已知m,n是
 的两个零点,记
的两个零点,记 为
为 的导函数,若
的导函数,若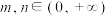 ,且
,且 ,证明:
,证明: .
.
您最近一年使用:0次
2023-12-20更新
|
473次组卷
|
4卷引用:江西省部分学校2024届高三上学期12月联考数学试题
名校
7 . 已知函数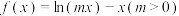 .
.
(1)若 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)若 有两个不同的零点
有两个不同的零点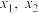 ,且
,且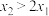 ,求实数
,求实数 的取值范围.
的取值范围.
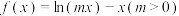 .
.(1)若
 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)若
 有两个不同的零点
有两个不同的零点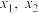 ,且
,且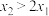 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-19更新
|
1210次组卷
|
5卷引用:江西省宜春市宜丰中学2024届高三上学期期末数学试题
8 . 已知函数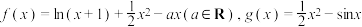 ,
,
(1)讨论 的单调性;
的单调性;
(2)若函数 与
与 的图象恰有一个交点,求
的图象恰有一个交点,求 的取值范围.
的取值范围.
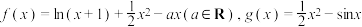 ,
,(1)讨论
 的单调性;
的单调性;(2)若函数
 与
与 的图象恰有一个交点,求
的图象恰有一个交点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-16更新
|
438次组卷
|
3卷引用:江西省赣州市南康中学2024届高三上学期"七省联考"考前数学猜题卷(十)
名校
解题方法
9 . 已知函数 ,则下列结论正确的有( )
,则下列结论正确的有( )
 ,则下列结论正确的有( )
,则下列结论正确的有( )A.当 时,方程 时,方程 存在实数根 存在实数根 |
B.当 时,函数 时,函数 在R上单调递减 在R上单调递减 |
C.当 时,函数 时,函数 有最小值,且最小值在 有最小值,且最小值在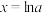 处取得 处取得 |
D.当 时,不等式 时,不等式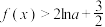 恒成立 恒成立 |
您最近一年使用:0次
2023-12-16更新
|
440次组卷
|
2卷引用:江西省上饶市广丰一中2024届高三上学期12月月考数学试题
名校
10 . 已知函数 .
.
(1)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)讨论函数 的零点个数.
的零点个数.
 .
.(1)若函数
 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(2)讨论函数
 的零点个数.
的零点个数.
您最近一年使用:0次
2023-12-01更新
|
535次组卷
|
4卷引用:江西省宜春市铜鼓中学2023届高三上学期第三次阶段性测试数学试题
江西省宜春市铜鼓中学2023届高三上学期第三次阶段性测试数学试题湖南省衡阳市第八中学等2024届高三上学期11月质量检测数学试题湖南省衡阳市第八中学2024届高三上学期11月质量检测数学试题(已下线)专题1.8 导数的零点问题(强化训练)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)



