解题方法
1 . 已知 是等差数列
是等差数列 的前
的前 项和,
项和, ,数列
,数列 是公比大于1的等比数列,且
是公比大于1的等比数列,且 ,
,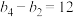 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设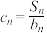 ,求使
,求使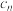 取得最大值时
取得最大值时 的值.
的值.
 是等差数列
是等差数列 的前
的前 项和,
项和, ,数列
,数列 是公比大于1的等比数列,且
是公比大于1的等比数列,且 ,
,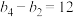 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)设
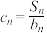 ,求使
,求使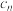 取得最大值时
取得最大值时 的值.
的值.
您最近一年使用:0次
解题方法
2 . 等比数列 中,
中, 为其前
为其前 项和,
项和, ,且
,且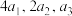 成等差数列,则
成等差数列,则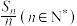 的最小值为( )
的最小值为( )
 中,
中, 为其前
为其前 项和,
项和, ,且
,且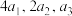 成等差数列,则
成等差数列,则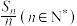 的最小值为( )
的最小值为( )A. | B.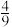 | C.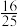 | D.1 |
您最近一年使用:0次
名校
解题方法
3 . 设数列 满足
满足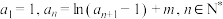 ,若对一切
,若对一切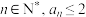 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
 满足
满足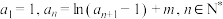 ,若对一切
,若对一切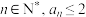 ,则实数
,则实数 的取值范围是( )
的取值范围是( )A. | B.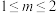 | C. | D.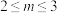 |
您最近一年使用:0次
解题方法
4 . 设无穷数列 的通项公式为
的通项公式为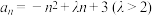 .若
.若 是单调递减数列,则
是单调递减数列,则 的一个取值为
的一个取值为____ .
 的通项公式为
的通项公式为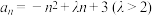 .若
.若 是单调递减数列,则
是单调递减数列,则 的一个取值为
的一个取值为
您最近一年使用:0次
5 . 在数列 中,
中, ,
, ,
,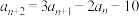 ,则
,则 的前n项和
的前n项和 的最大值为
的最大值为______ .
 中,
中, ,
, ,
,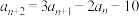 ,则
,则 的前n项和
的前n项和 的最大值为
的最大值为
您最近一年使用:0次
6 . 已知数列 的前n项和为
的前n项和为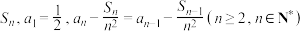 ,且关于n的不等式
,且关于n的不等式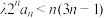 有3个解,则
有3个解,则 的取值范围是( )
的取值范围是( )
 的前n项和为
的前n项和为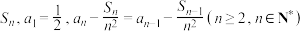 ,且关于n的不等式
,且关于n的不等式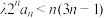 有3个解,则
有3个解,则 的取值范围是( )
的取值范围是( )A.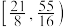 | B.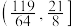 | C.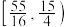 | D.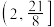 |
您最近一年使用:0次
7 . 已知数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,且
的等比数列,且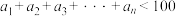 ,则
,则 的最大值为
的最大值为______ .
 是首项为
是首项为 ,公比为
,公比为 的等比数列,且
的等比数列,且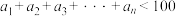 ,则
,则 的最大值为
的最大值为
您最近一年使用:0次
名校
解题方法
8 . 已知数列 的通项公式为
的通项公式为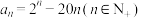 ,则数列
,则数列 中的最小项的值为
中的最小项的值为__________ .(用具体数字作答)
 的通项公式为
的通项公式为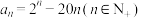 ,则数列
,则数列 中的最小项的值为
中的最小项的值为
您最近一年使用:0次
9 . 南宋数学家杨辉为我国古代数学研究作出了杰出贡献,他的著名研究成果 “杨辉三 角” 记录于其重要著作《详解九章算法》中, 该著作中的 “垛积术” 问题介绍了高 阶等差数列. 以高阶等差数列中的二阶等差数列为例,其特点是从数列中第二项开始,每一项与前一项的差构成等差数列. 若某个二阶等差数列  的前四项分别为:
的前四项分别为:  ,则下列说法错误的是( )
,则下列说法错误的是( )
 的前四项分别为:
的前四项分别为:  ,则下列说法错误的是( )
,则下列说法错误的是( )A. | B. |
C.数列  是单调递增数列 是单调递增数列 | D.数列 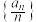 有最大项 有最大项 |
您最近一年使用:0次
解题方法
10 . 已知数列 的通项公式为
的通项公式为 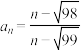 ,前
,前  项积为
项积为  ,则下列说法正确的是( )
,则下列说法正确的是( )
 的通项公式为
的通项公式为 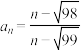 ,前
,前  项积为
项积为  ,则下列说法正确的是( )
,则下列说法正确的是( )A.在数列 中, 中, 是最大项 是最大项 | B.在数列 中, 中,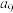 是最小项 是最小项 |
C.数列 单调递减 单调递减 | D.使 取得最小值的 取得最小值的 为 9 为 9 |
您最近一年使用:0次



