解题方法
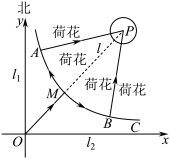
1 . 如图,某市建有贯穿东西和南北的两条垂直公路 ,
, ,在它们交叉路口点
,在它们交叉路口点 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线 上,
上, 与环形公路的交点记作
与环形公路的交点记作 .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路 先到达环形公路
先到达环形公路 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路 ,
, 的环形公路上选
的环形公路上选 ,
, 两处(
两处( ,
, 关于直线
关于直线 对称)修建直达观景台
对称)修建直达观景台 的玻璃栈道
的玻璃栈道 ,
, .以
.以 ,
, 所在的直线为
所在的直线为 ,
, 轴建立平面直角坐标系
轴建立平面直角坐标系 ,靠近公路
,靠近公路 ,
, 的环形公路可用曲线
的环形公路可用曲线 近似表示,曲线
近似表示,曲线 符合函数
符合函数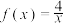 .
.
(1)若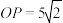 百米,点
百米,点 到
到 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道 的总长度;
的总长度;
(2)若要使得玻璃栈道 的总长度最小为
的总长度最小为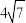 百米,求观景台
百米,求观景台 的位置.
的位置.
 ,
, ,在它们交叉路口点
,在它们交叉路口点 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线 上,
上, 与环形公路的交点记作
与环形公路的交点记作 .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路 先到达环形公路
先到达环形公路 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路 ,
, 的环形公路上选
的环形公路上选 ,
, 两处(
两处( ,
, 关于直线
关于直线 对称)修建直达观景台
对称)修建直达观景台 的玻璃栈道
的玻璃栈道 ,
, .以
.以 ,
, 所在的直线为
所在的直线为 ,
, 轴建立平面直角坐标系
轴建立平面直角坐标系 ,靠近公路
,靠近公路 ,
, 的环形公路可用曲线
的环形公路可用曲线 近似表示,曲线
近似表示,曲线 符合函数
符合函数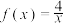 .
.
(1)若
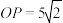 百米,点
百米,点 到
到 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道 的总长度;
的总长度;(2)若要使得玻璃栈道
 的总长度最小为
的总长度最小为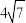 百米,求观景台
百米,求观景台 的位置.
的位置.
您最近一年使用:0次
2020-03-09更新
|
393次组卷
|
4卷引用:2020届江苏省苏州市张家港市高三阶段性调研测试数学试题
名校
2 . 已知函数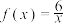 ,
, ,
,
(1)求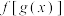 的解析式;
的解析式;
(2)关于 的不等式
的不等式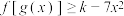 的解集为一切实数,求实数
的解集为一切实数,求实数 的取值范围;
的取值范围;
(3)关于 的不等式
的不等式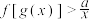 的解集中的正整数解恰有
的解集中的正整数解恰有 个,求实数
个,求实数 的取值范围.
的取值范围.
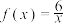 ,
, ,
,(1)求
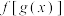 的解析式;
的解析式;(2)关于
 的不等式
的不等式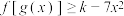 的解集为一切实数,求实数
的解集为一切实数,求实数 的取值范围;
的取值范围;(3)关于
 的不等式
的不等式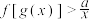 的解集中的正整数解恰有
的解集中的正整数解恰有 个,求实数
个,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-03-05更新
|
2273次组卷
|
2卷引用:上海市上海外国语大学附属外国语学校2015-2016学年高一上学期期末数学试题
名校
解题方法
3 . 已知函数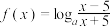 (
( 且
且 ).
).
(1)求函数 的定义域,并求出当
的定义域,并求出当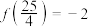 时,常数
时,常数 的值;
的值;
(2)在(1)的条件下,判断函数 在
在 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)设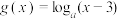 ,若方程
,若方程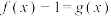 有实根,求
有实根,求 的取值范围.
的取值范围.
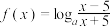 (
( 且
且 ).
).(1)求函数
 的定义域,并求出当
的定义域,并求出当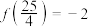 时,常数
时,常数 的值;
的值;(2)在(1)的条件下,判断函数
 在
在 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;(3)设
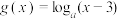 ,若方程
,若方程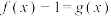 有实根,求
有实根,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-03-04更新
|
429次组卷
|
2卷引用:广东省汕头市金山中学2019-2020学年高一上学期期中数学试题
解题方法
4 . 已知函数 ,
,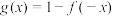 ,且
,且 是R上的奇函数,
是R上的奇函数,
(1)求实数a的值;
(2)判断函数 )的单调性(不必说明理由),并求不等式
)的单调性(不必说明理由),并求不等式 的解集;
的解集;
(3)若不等式 对任意的
对任意的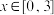 恒成立,求实数b的取值范围.
恒成立,求实数b的取值范围.
 ,
,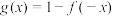 ,且
,且 是R上的奇函数,
是R上的奇函数,(1)求实数a的值;
(2)判断函数
 )的单调性(不必说明理由),并求不等式
)的单调性(不必说明理由),并求不等式 的解集;
的解集;(3)若不等式
 对任意的
对任意的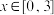 恒成立,求实数b的取值范围.
恒成立,求实数b的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 已知奇函数f(x)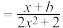 ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ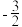 ,θ∈[m,
,θ∈[m, ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
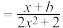 ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ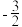 ,θ∈[m,
,θ∈[m, ].m,b∈R.
].m,b∈R.(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
您最近一年使用:0次
2020-03-04更新
|
436次组卷
|
2卷引用:江苏省无锡市江阴市2019-2020学年高一上学期期末数学试题
名校
解题方法
6 . 已知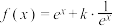 ,
,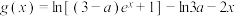 .
.
(1)若函数 在
在 为增函数,求实数
为增函数,求实数 的值;
的值;
(2)若函数 为偶函数,对于任意
为偶函数,对于任意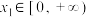 ,任意
,任意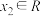 ,使得
,使得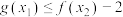 成立,求
成立,求 的取值范围.
的取值范围.
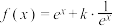 ,
,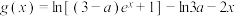 .
.(1)若函数
 在
在 为增函数,求实数
为增函数,求实数 的值;
的值;(2)若函数
 为偶函数,对于任意
为偶函数,对于任意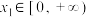 ,任意
,任意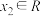 ,使得
,使得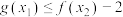 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-03-03更新
|
2682次组卷
|
8卷引用:四川省绵阳市三台中学实验学校2019-2020学年高一上学期期末数学试题
名校
7 . 若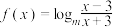 ,设其定义域上的区间
,设其定义域上的区间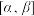 (
(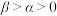 ).
).
(1)判断该函数的奇偶性,并证明;
(2)当 时,判断函数在区间
时,判断函数在区间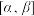 (
(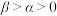 )上的单调性,并证明;
)上的单调性,并证明;
(3)当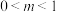 时,若存在区间
时,若存在区间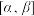 (
(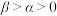 ),使函数
),使函数 在该区间上的值域为
在该区间上的值域为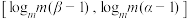 ,求实数
,求实数 的取值范围.
的取值范围.
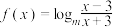 ,设其定义域上的区间
,设其定义域上的区间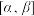 (
(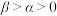 ).
).(1)判断该函数的奇偶性,并证明;
(2)当
 时,判断函数在区间
时,判断函数在区间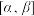 (
(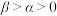 )上的单调性,并证明;
)上的单调性,并证明;(3)当
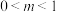 时,若存在区间
时,若存在区间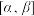 (
(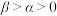 ),使函数
),使函数 在该区间上的值域为
在该区间上的值域为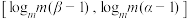 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-03-02更新
|
627次组卷
|
2卷引用:上海市上海外国语附属外国语学校2018-2019学年高一下学期3月月考数学试题
解题方法
8 . 若存在常数 ,使得对任意
,使得对任意 ,
, ,均有
,均有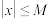 ,则称
,则称 为有界集合,同时称
为有界集合,同时称 为集合
为集合 的上界.
的上界.
(1)设 ,
,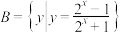 ,试判断
,试判断 是否为有界集合,并说明理由;
是否为有界集合,并说明理由;
(2)已知常数 ,若函数
,若函数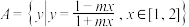 为有界集合,求集合
为有界集合,求集合 的上界
的上界 最小值
最小值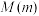 .
.
(3)已知函数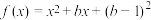 ,记
,记 ,
,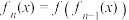 ,
, ,
, ,求使得集合
,求使得集合 为有界集合时
为有界集合时 的取值范围.
的取值范围.
 ,使得对任意
,使得对任意 ,
, ,均有
,均有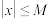 ,则称
,则称 为有界集合,同时称
为有界集合,同时称 为集合
为集合 的上界.
的上界.(1)设
 ,
,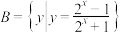 ,试判断
,试判断 是否为有界集合,并说明理由;
是否为有界集合,并说明理由;(2)已知常数
 ,若函数
,若函数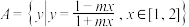 为有界集合,求集合
为有界集合,求集合 的上界
的上界 最小值
最小值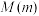 .
.(3)已知函数
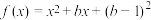 ,记
,记 ,
,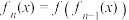 ,
, ,
, ,求使得集合
,求使得集合 为有界集合时
为有界集合时 的取值范围.
的取值范围.
您最近一年使用:0次
名校
9 . 国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,新标准规定,车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下:
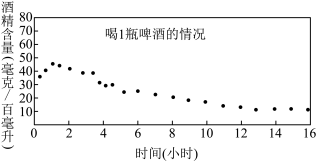
该函数模型如下,
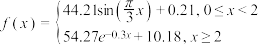 .
.
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据: )
)

该函数模型如下,
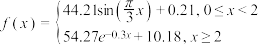 .
.根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据:
 )
)
您最近一年使用:0次
2020-03-02更新
|
1872次组卷
|
12卷引用:湖北省襄阳市2018-2019学年高一上学期期末数学试题
湖北省襄阳市2018-2019学年高一上学期期末数学试题河北省石家庄市藁城区第一中学2019-2020学年高一上学期第三次月考数学试题湖北省武汉市武昌实验中学2020-2021学年高一上学期12月月考数学试题(已下线)8.2 函数与数学模型黑龙江省大兴安岭实验中学(东校区)2021-2022学年高一上学期期中考试数学试题湖北省武汉市华中科技大学附属中学2021-2022学年高一上学期12月月考数学试题湖南师范大学附属中学2021-2022学年高一上学期期末数学试题湖北省黄冈市红安县第一中学2021-2022学年高一下学期开学检测数学试题新疆岳普湖县2021-2022学年高一下学期第一次学情调研测试数学试题云南省北大附中云南实验学校2020-2021学年高一下学期期中考试数学试题(已下线)7.4 三角函数的应用-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)安徽省宿州市省、市示范高中2023-2024学年高一上学期期末教学质量检测数学试题
名校
10 . 已知二次函数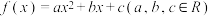 的最小值为-1,且关于
的最小值为-1,且关于 的方程
的方程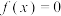 的两根为0和-2.
的两根为0和-2.
(1)求函数 的解析式;
的解析式;
(2)设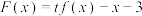 其中
其中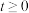 ,求函数
,求函数 在
在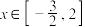 时的最大值
时的最大值 ;
;
(3)若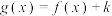 (
( 为实数),对任意
为实数),对任意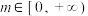 ,总存在
,总存在 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
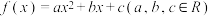 的最小值为-1,且关于
的最小值为-1,且关于 的方程
的方程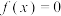 的两根为0和-2.
的两根为0和-2. (1)求函数
 的解析式;
的解析式;(2)设
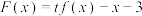 其中
其中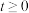 ,求函数
,求函数 在
在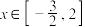 时的最大值
时的最大值 ;
;(3)若
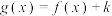 (
( 为实数),对任意
为实数),对任意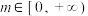 ,总存在
,总存在 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-03-02更新
|
603次组卷
|
5卷引用:四川省成都市田家炳中学2018-2019学年高一上学期期中数学试题



