2024高三下·江苏·专题练习
解题方法
1 . 已知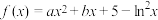 ,当
,当 时,若
时,若 有两个极值点
有两个极值点 ,求证:
,求证: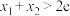 .
.
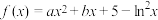 ,当
,当 时,若
时,若 有两个极值点
有两个极值点 ,求证:
,求证: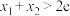 .
.
您最近半年使用:0次
2 . 已知函数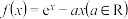 (
( 为自然对数的底数).
为自然对数的底数).
(1)求函数 的单调区间;
的单调区间;
(2)若 ,
,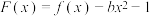 的导数
的导数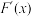 在
在 上是增函数,求实数b的最大值;
上是增函数,求实数b的最大值;
(3)在(2)的条件下,求证: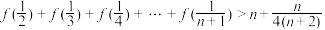 对一切正整数
对一切正整数 均成立.
均成立.
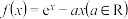 (
( 为自然对数的底数).
为自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)若
 ,
,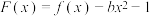 的导数
的导数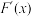 在
在 上是增函数,求实数b的最大值;
上是增函数,求实数b的最大值;(3)在(2)的条件下,求证:
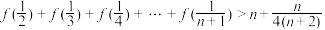 对一切正整数
对一切正整数 均成立.
均成立.
您最近半年使用:0次
2024·全国·模拟预测
3 . 若函数 在
在 上满足
上满足 且不恒为0,则称函数
且不恒为0,则称函数 为区间
为区间 上的绝对增函数,
上的绝对增函数, 称为函数
称为函数 的特征函数,称任意的实数
的特征函数,称任意的实数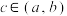 为绝对增点(
为绝对增点( 为函数
为函数 的导函数).
的导函数).
(1)若1为函数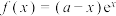 的绝对增点,求
的绝对增点,求 的取值范围;
的取值范围;
(2)绝对增函数 的特征函数
的特征函数 的唯一零点为
的唯一零点为 .
.
(ⅰ)证明: 是
是 的极值点;
的极值点;
(ⅱ)证明: 不是绝对增函数.
不是绝对增函数.
 在
在 上满足
上满足 且不恒为0,则称函数
且不恒为0,则称函数 为区间
为区间 上的绝对增函数,
上的绝对增函数, 称为函数
称为函数 的特征函数,称任意的实数
的特征函数,称任意的实数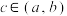 为绝对增点(
为绝对增点( 为函数
为函数 的导函数).
的导函数).(1)若1为函数
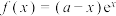 的绝对增点,求
的绝对增点,求 的取值范围;
的取值范围;(2)绝对增函数
 的特征函数
的特征函数 的唯一零点为
的唯一零点为 .
.(ⅰ)证明:
 是
是 的极值点;
的极值点;(ⅱ)证明:
 不是绝对增函数.
不是绝对增函数.
您最近半年使用:0次
4 . 材料一:有理数都能表示成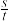 ,(
,(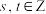 ,且
,且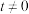 ,s与t互质)的形式,进而有理数集可以表示为{
,s与t互质)的形式,进而有理数集可以表示为{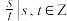 且
且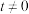 ,s与t互质}.
,s与t互质}.
材料二:我们知道.当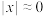 时,可以用一次多项式近似表达指数函数,即
时,可以用一次多项式近似表达指数函数,即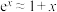 ;为提高精确度.可以用更高次的多项式逼近指数函数.
;为提高精确度.可以用更高次的多项式逼近指数函数.
设 对等式两边求导,
对等式两边求导,
得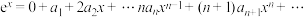
对比各项系数,可得: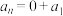 ,
,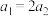 ,
, ,…,
,…, ;
;
所以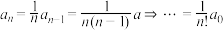 ,取
,取 ,有
,有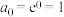 ,
,
代回原式: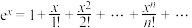 .
.
材料三:对于公比为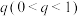 的等比数列
的等比数列 ,当
,当 时,数列
时,数列 的前n项和
的前n项和 .
.
阅读上述材料,完成以下两个问题:
(1)证明:无限循环小数3.7为有理数;
(2)用反证法证明:e为无理数(e=2.7182^为自然对数底数).
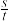 ,(
,(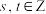 ,且
,且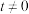 ,s与t互质)的形式,进而有理数集可以表示为{
,s与t互质)的形式,进而有理数集可以表示为{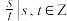 且
且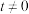 ,s与t互质}.
,s与t互质}.材料二:我们知道.当
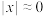 时,可以用一次多项式近似表达指数函数,即
时,可以用一次多项式近似表达指数函数,即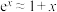 ;为提高精确度.可以用更高次的多项式逼近指数函数.
;为提高精确度.可以用更高次的多项式逼近指数函数. 设
 对等式两边求导,
对等式两边求导,得
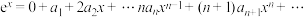
对比各项系数,可得:
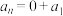 ,
,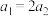 ,
, ,…,
,…, ;
;所以
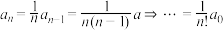 ,取
,取 ,有
,有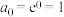 ,
,代回原式:
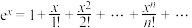 .
.材料三:对于公比为
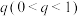 的等比数列
的等比数列 ,当
,当 时,数列
时,数列 的前n项和
的前n项和 .
.阅读上述材料,完成以下两个问题:
(1)证明:无限循环小数3.7为有理数;
(2)用反证法证明:e为无理数(e=2.7182^为自然对数底数).
您最近半年使用:0次
名校
解题方法
5 . 已知 ,
,
(1)当 时,求
时,求 在点
在点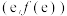 处的切线方程;
处的切线方程;
(2)讨论 的单调性;
的单调性;
(3)若函数 存在极大值,且极大值为1,求证:
存在极大值,且极大值为1,求证: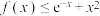 .
.
 ,
,(1)当
 时,求
时,求 在点
在点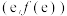 处的切线方程;
处的切线方程;(2)讨论
 的单调性;
的单调性;(3)若函数
 存在极大值,且极大值为1,求证:
存在极大值,且极大值为1,求证: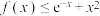 .
.
您最近半年使用:0次
名校
6 . 已知函数 .
.
(1)当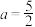 时,判断
时,判断 的单调性;
的单调性;
(2)若 存在两个极值点
存在两个极值点 ,
, ,且
,且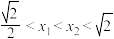 ,求证:
,求证: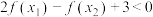 .
.
 .
.(1)当
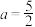 时,判断
时,判断 的单调性;
的单调性;(2)若
 存在两个极值点
存在两个极值点 ,
, ,且
,且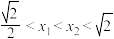 ,求证:
,求证: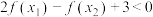 .
.
您最近半年使用:0次
名校
7 . 设函数 与
与 的定义域为
的定义域为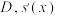 与
与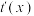 分别为函数
分别为函数 与
与 的导函数,若存在
的导函数,若存在 ,满足
,满足 且
且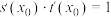 ,则称函数
,则称函数 与
与 为“优美函数”.已知函数
为“优美函数”.已知函数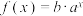 与
与 .
.
(1)已知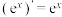 和
和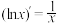 ,求证:
,求证: 和
和 ;
;
(2)当 时,若函数
时,若函数 与
与 为“优美函数”,求
为“优美函数”,求 的取值范围;
的取值范围;
(3)当 时,已知函数
时,已知函数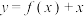 与
与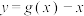 为“优美函数”,求证:
为“优美函数”,求证: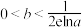 .
.
 与
与 的定义域为
的定义域为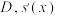 与
与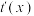 分别为函数
分别为函数 与
与 的导函数,若存在
的导函数,若存在 ,满足
,满足 且
且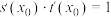 ,则称函数
,则称函数 与
与 为“优美函数”.已知函数
为“优美函数”.已知函数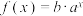 与
与 .
.(1)已知
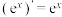 和
和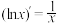 ,求证:
,求证: 和
和 ;
;(2)当
 时,若函数
时,若函数 与
与 为“优美函数”,求
为“优美函数”,求 的取值范围;
的取值范围;(3)当
 时,已知函数
时,已知函数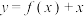 与
与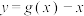 为“优美函数”,求证:
为“优美函数”,求证: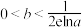 .
.
您最近半年使用:0次
名校
8 . 根据多元微分求条件极值理论,要求二元函数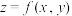 在约束条件
在约束条件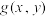 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数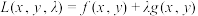 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对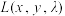 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下:
 ,解此方程组,得出解
,解此方程组,得出解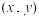 ,就是二元函数
,就是二元函数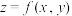 在约束条件
在约束条件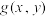 的可能极值点.
的可能极值点. 的值代入到
的值代入到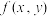 中即为极值.
中即为极值.
补充说明:【例】求函数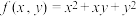 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的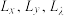 表示分别对
表示分别对 进行求导.
进行求导.
(1)求函数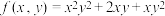 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.
(2)利用拉格朗日乘数法求:设实数 满足
满足 ,求
,求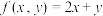 的最大值.
的最大值.
(3)①若 为实数,且
为实数,且 ,证明:
,证明: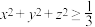 .
.
②设 ,求
,求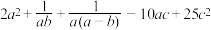 的最小值.
的最小值.
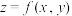 在约束条件
在约束条件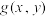 的可能极值点,首先构造出一个拉格朗日辅助函数
的可能极值点,首先构造出一个拉格朗日辅助函数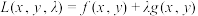 ,其中
,其中 为拉格朗日系数.分别对
为拉格朗日系数.分别对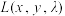 中的
中的 部分求导,并使之为0,得到三个方程组,如下:
部分求导,并使之为0,得到三个方程组,如下: ,解此方程组,得出解
,解此方程组,得出解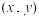 ,就是二元函数
,就是二元函数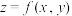 在约束条件
在约束条件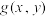 的可能极值点.
的可能极值点. 的值代入到
的值代入到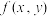 中即为极值.
中即为极值.补充说明:【例】求函数
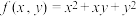 关于变量
关于变量 的导数.即:将变量
的导数.即:将变量 当做常数,即:
当做常数,即: ,下标加上
,下标加上 ,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的
,代表对自变量x进行求导.即拉格朗日乘数法方程组之中的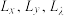 表示分别对
表示分别对 进行求导.
进行求导.(1)求函数
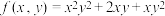 关于变量
关于变量 的导数并求当
的导数并求当 处的导数值.
处的导数值.(2)利用拉格朗日乘数法求:设实数
 满足
满足 ,求
,求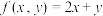 的最大值.
的最大值.(3)①若
 为实数,且
为实数,且 ,证明:
,证明: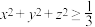 .
.②设
 ,求
,求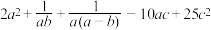 的最小值.
的最小值.
您最近半年使用:0次
名校
9 . 已知函数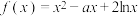 ,
, .
.
(1)讨论 的单调性;
的单调性;
(2)已知 有两个极值点
有两个极值点 ,且
,且 ,证明:
,证明: .
.
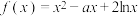 ,
, .
.(1)讨论
 的单调性;
的单调性;(2)已知
 有两个极值点
有两个极值点 ,且
,且 ,证明:
,证明: .
.
您最近半年使用:0次
2023-11-23更新
|
332次组卷
|
2卷引用:山东省临沂市2023-2024学年高三上学期期中考试数学试题
名校
10 . 已知曲线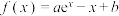 在
在 处的切线过点
处的切线过点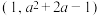 .
.
(1)试求 ,
, 满足的关系式;(用
满足的关系式;(用 表示
表示 )
)
(2)讨论 的单调性;
的单调性;
(3)证明:当 时,
时,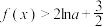 .
.
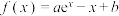 在
在 处的切线过点
处的切线过点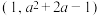 .
.(1)试求
 ,
, 满足的关系式;(用
满足的关系式;(用 表示
表示 )
)(2)讨论
 的单调性;
的单调性;(3)证明:当
 时,
时,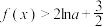 .
.
您最近半年使用:0次
2024-04-01更新
|
510次组卷
|
3卷引用:江苏省江都中学2023-2024学年高二下学期3月联考数学试卷



