名校
解题方法
1 . 如图,在四棱锥 中,
中, 底面
底面 ,底面
,底面 为正方形,
为正方形, ,
, 为
为 的中点,
的中点, 为
为 的中点,则异面直线
的中点,则异面直线 与
与 所成角的正弦值为( )
所成角的正弦值为( )
 中,
中, 底面
底面 ,底面
,底面 为正方形,
为正方形, ,
, 为
为 的中点,
的中点, 为
为 的中点,则异面直线
的中点,则异面直线 与
与 所成角的正弦值为( )
所成角的正弦值为( )
A. | B.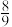 | C. | D.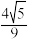 |
您最近一年使用:0次
2021-10-19更新
|
935次组卷
|
20卷引用:专题9.6—立体几何—异面直线所成的角2—2022届高三数学一轮复习精讲精练
(已下线)专题9.6—立体几何—异面直线所成的角2—2022届高三数学一轮复习精讲精练湖湘大联考2021-2022学年高二上学期10月月考数学试题吉林省四平市第一高级中学2021-2022学年高二上学期10月月考数学试题山西省大同市新世纪中学2021-2022学年高二上学期第一次月考数学试题湖南省郴州市嘉禾县第一中学2021-2022学年高二上学期9月月考数学试题(已下线)期中考试模拟卷02-【一堂好课】2021-2022学年高二数学上学期同步精品课堂(人教A版2019选择性必修第一册)湖北省鄂东南三校联考2021-2022学年高二上学期阶段考试(一)数学试题重庆市万州清泉中学2022-2023学年高二上学期9月月考数学试题河南省郑州市第二高级中学2022-2023学年高二上学期10月月考数学试题河南省商城县观庙高级中学2022-2023学年高二上学期第一次月考理科数学试题浙江省温州市平阳县万全综合高级中学2022-2023学年高二上学期10月检测数学试题重庆市涪陵第二中学校2022-2023学年高二上学期第一次月考数学试题新疆石河子第一中学2022-2023学年高二上学期10月月考数学(理)试题安徽省芜湖市无为襄安中学2022-2023学年高二上学期11月期中数学试题安徽省合肥市庐江县第五中学(庐巢八校联考)2022-2023学年高二上学期12月月考数学试题黑龙江省绥化市绥棱县第一中学2023-2024学年高二上学期9月月考数学试题山西省运城市稷山县稷山中学2023-2024学年高二上学期11月月考数学试题河北省深州中学2023-2024学年高二上学期期末考试数学试题山西省介休市第一中学校2022-2023学年高二上学期开学考试数学试题西藏山南市普通高中2023-2024学年高二上学期期末考试数学试题
名校
2 . 如图,在三棱柱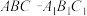 中,点E,F分别在棱
中,点E,F分别在棱 ,
, 上(均异于端点),
上(均异于端点), ,
, ,
,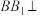 平面
平面 .
.
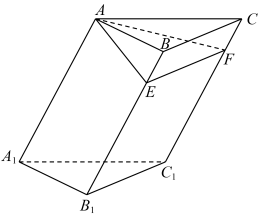
(1)求证:四边形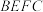 是矩形;
是矩形;
(2)若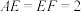 ,
,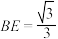 ,求平面
,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
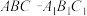 中,点E,F分别在棱
中,点E,F分别在棱 ,
, 上(均异于端点),
上(均异于端点), ,
, ,
,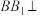 平面
平面 .
.
(1)求证:四边形
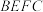 是矩形;
是矩形;(2)若
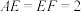 ,
,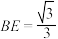 ,求平面
,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
您最近一年使用:0次
2021-09-18更新
|
1741次组卷
|
4卷引用:湖北省新高考九师联盟2021届高三下学期2月质检巩固数学试题
湖北省新高考九师联盟2021届高三下学期2月质检巩固数学试题(已下线)专题04 二面角(含探索性问题)-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)四川省内江市第六中学2022届高三下学期考前强化训练二数学(理科)试题黑龙江省哈尔滨市第三中学2021-2022学年高二上学期10月月考数学试题
3 . 在四棱锥 中,
中, 平面
平面 ,
, ,
, ,
,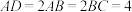 ,
, 为
为 的中点,
的中点, 为
为 的中点
的中点 .
.

(Ⅰ)线段 上是否存在点
上是否存在点 ,使得
,使得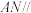 平面
平面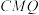 ?若存在,指出点
?若存在,指出点 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;
(Ⅱ)若异面直线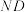 与
与 所成角的余弦值为
所成角的余弦值为 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
 中,
中, 平面
平面 ,
, ,
, ,
,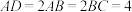 ,
, 为
为 的中点,
的中点, 为
为 的中点
的中点 .
.
(Ⅰ)线段
 上是否存在点
上是否存在点 ,使得
,使得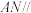 平面
平面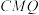 ?若存在,指出点
?若存在,指出点 的位置;若不存在,请说明理由;
的位置;若不存在,请说明理由;(Ⅱ)若异面直线
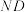 与
与 所成角的余弦值为
所成角的余弦值为 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
您最近一年使用:0次
名校
4 . 已知四棱锥 中,
中, 平面
平面 ,且
,且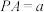 ,底面
,底面 是边长为b的菱形,
是边长为b的菱形, .
.
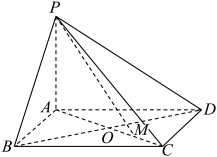
(1)求证:平面 平面
平面 ;
;
(2)设 与
与 交于点
交于点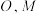 为
为 中点,若二面角
中点,若二面角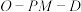 的正切值是
的正切值是 ,求
,求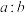 的值.
的值.
 中,
中, 平面
平面 ,且
,且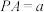 ,底面
,底面 是边长为b的菱形,
是边长为b的菱形, .
.
(1)求证:平面
 平面
平面 ;
;(2)设
 与
与 交于点
交于点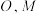 为
为 中点,若二面角
中点,若二面角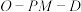 的正切值是
的正切值是 ,求
,求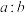 的值.
的值.
您最近一年使用:0次
2021-09-13更新
|
1159次组卷
|
3卷引用:山东省师范大学附属中学2021-2022学年高三上学期开学考试数学试题
山东省师范大学附属中学2021-2022学年高三上学期开学考试数学试题广东省汕头市澄海中学2022届高三上学期第一学段考试数学试题(已下线)第35讲 利用传统方法解决立体几何中的角度与距离问题-2022年新高考数学二轮专题突破精练
5 . 在四棱锥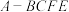 中,底面
中,底面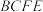 为梯形﹐
为梯形﹐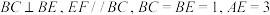 ,
,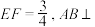 平面
平面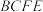 .
.
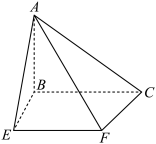
(1)证明:平面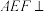 平面
平面 ;
;
(2)求直线 与平面
与平面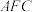 所成角的正弦值.
所成角的正弦值.
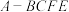 中,底面
中,底面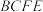 为梯形﹐
为梯形﹐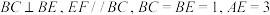 ,
,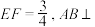 平面
平面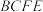 .
.
(1)证明:平面
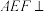 平面
平面 ;
;(2)求直线
 与平面
与平面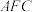 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2021-09-13更新
|
2126次组卷
|
8卷引用:神州智达省级联测2021-2022学年高三上学期第一次考试数学试题
神州智达省级联测2021-2022学年高三上学期第一次考试数学试题河北省省级联测2022届高三上学期第一次考试数学试题(已下线)专题03 直线与平面所成角(含探索性问题)-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)黑龙江省牡丹江市海林市朝鲜族中学2022-2023学年高三上学期第三次月考数学(理)试题黑龙江省七台河市勃利县高级中学2021-2022学年高二上学期9月月考数学试题山西省太原市第五十六中学校2022-2023学年高二上学期10月联考数学试题安徽省阜阳市阜南实验中学2022-2023学年高二上学期第二次质量检测数学试题广东省兴宁市沐彬中学2022-2023学年高二上学期第二次月考数学试题
名校
解题方法
6 . 如图,在三棱台 中,平面
中,平面 平面
平面 ,
,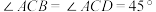 ,
,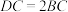 .
.

(1)证明: ;
;
(2)求二面角 的正弦值.
的正弦值.
 中,平面
中,平面 平面
平面 ,
,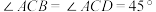 ,
,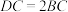 .
.
(1)证明:
 ;
;(2)求二面角
 的正弦值.
的正弦值.
您最近一年使用:0次
2021-09-12更新
|
1253次组卷
|
3卷引用:第34讲 利用坐标法解决立体几何的角度与距离问题-2022年新高考数学二轮专题突破精练
(已下线)第34讲 利用坐标法解决立体几何的角度与距离问题-2022年新高考数学二轮专题突破精练重庆市第十八中学2020-2021学年高二下学期3月月考数学试题广东省深圳市布吉中学2021-2022学年高二上学期期中数学试题
解题方法
7 . 如图,四棱锥 的底面为矩形,
的底面为矩形,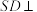 底面
底面 ,设平面
,设平面 与平面
与平面 的交线为m.
的交线为m.
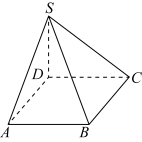
(1)证明: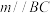 ,且
,且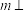 平面
平面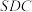 ;
;
(2)已知 ,R为m上的点求
,R为m上的点求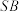 与平面
与平面 所成角的余弦值的最小值.
所成角的余弦值的最小值.
 的底面为矩形,
的底面为矩形,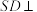 底面
底面 ,设平面
,设平面 与平面
与平面 的交线为m.
的交线为m.
(1)证明:
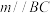 ,且
,且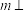 平面
平面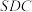 ;
;(2)已知
 ,R为m上的点求
,R为m上的点求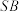 与平面
与平面 所成角的余弦值的最小值.
所成角的余弦值的最小值.
您最近一年使用:0次
名校
解题方法
8 . 如图,直三棱柱 的侧面
的侧面 为矩形,
为矩形,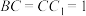 ,
,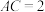 ,
, .
.
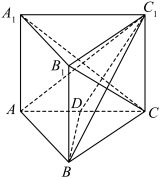
(1)求证:平面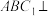 平面
平面 ;
;
(2)设 为
为 的中点,求平面
的中点,求平面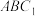 与平面
与平面 所成锐角的余弦值.
所成锐角的余弦值.
 的侧面
的侧面 为矩形,
为矩形,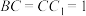 ,
,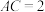 ,
, .
.
(1)求证:平面
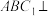 平面
平面 ;
;(2)设
 为
为 的中点,求平面
的中点,求平面 与平面
与平面 所成锐角的余弦值.
所成锐角的余弦值.
您最近一年使用:0次
2021-09-09更新
|
960次组卷
|
2卷引用:四川省成都市蒲江县蒲江中学2020年高三上学期11月月考数学(理)试题
名校
9 . 如图在三棱锥P-ABC中,平面PAB⊥平面PBC,PB⊥BC,PD=DB=BC=AB=AD=2.
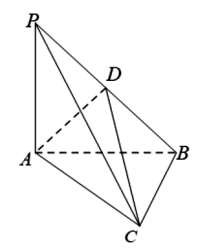
(1)证明:PA⊥平面ABC;
(2)求二面角B-AD-C的余弦值.

(1)证明:PA⊥平面ABC;
(2)求二面角B-AD-C的余弦值.
您最近一年使用:0次
2021-09-05更新
|
1545次组卷
|
4卷引用:安徽省名校联盟2021-2022学年高三上学期开学考试理科数学试题
安徽省名校联盟2021-2022学年高三上学期开学考试理科数学试题(已下线)2021年全国高考甲卷数学(理)试题变式题16-20题(已下线)2021年全国高考甲卷数学(理)试题变式题16-20题海南省琼海市嘉积中学2021-2022学年高一下学期期末数学试题
名校
解题方法
10 . 如图,棱长为1的正方体 中,
中, 为线段
为线段 上的动点(不含端点),则下列结论正确的是( )
上的动点(不含端点),则下列结论正确的是( )

 中,
中, 为线段
为线段 上的动点(不含端点),则下列结论正确的是( )
上的动点(不含端点),则下列结论正确的是( )
A.直线 与 与 所成的角可能是 所成的角可能是 |
B.平面 平面 平面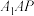 |
C.三棱锥 的体积为定值 的体积为定值 |
D.平面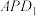 截正方体所得的截面可能是等腰梯形 截正方体所得的截面可能是等腰梯形 |
您最近一年使用:0次
2021-09-04更新
|
2198次组卷
|
6卷引用:河北省衡水市武邑中学2024届高三上学期第三次调研考试数学试题



