名校
解题方法
1 . 手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间.为
了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各7台,在相同条件下进行测试,统计结果如下:
其中, ,
, 是正整数,且
是正整数,且 .
.
(1)该卖场有56台A型手机,试估计其中待机时间不少于123小时的台数;
(2)从A型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为 ,求
,求 的分布列;
的分布列;
(3)设A,B两个型号被测试手机待机时间的平均值相等,当B型号被测试手机待机时间的方差最小时,写出 ,
, 的值(结论不要求证明).
的值(结论不要求证明).
了解A,B两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A,B两个型号的手机各7台,在相同条件下进行测试,统计结果如下:
手机编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
A型待机时间 | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
B型待机时间 | 118 | 123 | 127 | 120 | 124 |
|
|
 ,
, 是正整数,且
是正整数,且 .
.(1)该卖场有56台A型手机,试估计其中待机时间不少于123小时的台数;
(2)从A型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为
 ,求
,求 的分布列;
的分布列;(3)设A,B两个型号被测试手机待机时间的平均值相等,当B型号被测试手机待机时间的方差最小时,写出
 ,
, 的值(结论不要求证明).
的值(结论不要求证明).
您最近一年使用:0次
2024-05-22更新
|
240次组卷
|
2卷引用:河北省邢台市南宫中学2024届高三下学期高考模拟数学试题
名校
2 . 一个1,两个2,三个3组成一个六位数,则相同数字不相邻的个数为__________ .相同数字不相邻的概率为__________ .
您最近一年使用:0次
2024-05-20更新
|
564次组卷
|
3卷引用:河北省邢台市南宫中学2024届高三下学期高考模拟数学试题
名校
解题方法
3 . 中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设 ,
, ,
,
 为整数,若
为整数,若 和
和 同时除以
同时除以 所得的余数相同,则称
所得的余数相同,则称 和
和 对模
对模 同余,记为
同余,记为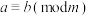 .若
.若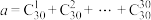 ,
, ,则
,则 的值可以是( )
的值可以是( )
 ,
, ,
,
 为整数,若
为整数,若 和
和 同时除以
同时除以 所得的余数相同,则称
所得的余数相同,则称 和
和 对模
对模 同余,记为
同余,记为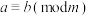 .若
.若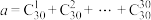 ,
, ,则
,则 的值可以是( )
的值可以是( )| A.2021 | B.2022 | C.2023 | D.2024 |
您最近一年使用:0次
2024-05-19更新
|
693次组卷
|
5卷引用:【练】专题二 二项式定理应用问题(压轴大全)
(已下线)【练】专题二 二项式定理应用问题(压轴大全)(已下线)7.2 二项式定理河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题(已下线)第五章 概率统计创新问题 专题七 概率统计中的新定义问题 微点1 概率统计中的新定义问题(一)【培优版】江西省上饶市稳派上进六校联考2024届高三5月第二次联合考试数学试题
名校
解题方法
4 . 下列说法正确的是( )
A.设A,B为两个事件,且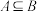 , ,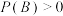 ,则 ,则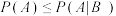 |
B.若变量x与变量y满足关系 ,变量y与变量z是正相关,则x与z负相关 ,变量y与变量z是正相关,则x与z负相关 |
| C.若在一组数据2,3,3,4,6中增加一个数据4,则方差变小 |
D.根据分类变量X与Y的成对样本数据,计算得到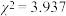 ,根据小概率值 ,根据小概率值 的独立性检验( 的独立性检验( ),可判断X与Y有关联,此推断犯错的概率不大于0.05 ),可判断X与Y有关联,此推断犯错的概率不大于0.05 |
您最近一年使用:0次
2024-05-19更新
|
776次组卷
|
3卷引用:河北省邢台市南宫中学2023-2024学年高三高考考前定心卷3数学试题
名校
5 . 已知盒子中有6个大小相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两球,每次取一球,记第一次取出的球的数字是 ,第二次取出的球的数字是
,第二次取出的球的数字是 .若事件
.若事件 “
“ 为偶数”,事件
为偶数”,事件 “
“ ,
, 中有偶数且
中有偶数且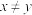 ”,则
”,则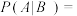 ( )
( )
 ,第二次取出的球的数字是
,第二次取出的球的数字是 .若事件
.若事件 “
“ 为偶数”,事件
为偶数”,事件 “
“ ,
, 中有偶数且
中有偶数且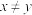 ”,则
”,则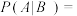 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2024-05-12更新
|
947次组卷
|
7卷引用:专题1 现实生活情境
(已下线)专题1 现实生活情境(已下线)易错点9 概率类型定不准致误河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题(已下线)专题4 古典概型 分别计数(经典好题母题)【讲】陕西省渭南市临渭区2024届高三下学期质量检测(三模)文科数学试题黑龙江省大庆市2023-2024学年高三下学期第三次教学质量检测数学试卷四川省成都列五中学2024-2025学年高三上学期入学摸底测试数学试题
名校
6 . 在对于一些敏感性问题调查时,被调查者往往不愿意给出真实答复,因此需要特别的调查方法消除被调查者的顾虑,使他们能如实回答问题.某单位为提升员工的工作效率,规范管理,决定出台新的员工考勤管理方案,方案起草后,为了解员工对新方案是否满意,决定采取如下随机化回答技术进行问卷调查:随机选取150名男员工和150名女员工进行问卷调查.问卷调查中设置了两个问题:①你公历生日是奇数吗?②你对新考勤管理方案是否满意.调查分两个环节,第一个环节:确定回答的问题,让被调查者从装有4个红球,6个黑球(除颜色外完全相同)的袋子中随机摸取两个球.摸到两球同色的员工如实回答第一个问题,摸到两球异色的员工如实回答第二个问题,第二个环节:填写问卷(问卷中不含问题,只有“是”与“否”).已知统计问卷中有198个“是”.(参考数据: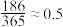 )
)
(1)根据以上的调查结果,利用你所学的知识,估计员工对新考勤管理方案满意的概率 ;
;
(2)据核实,以上的300名员工中有15名员工对新考勤管理方案不满意,其中男3人,女12人,试判断是否有97.5%的把握认为与对新考勤管理方案是否满意与性别有关;
参考公式和数据如下: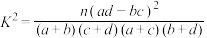 ,
, .
.
(3)从该单位任取10人,恰有X人对考勤管理方案不满意,利用(1)中的结果,写出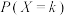 的表达式(其中
的表达式(其中 ,
,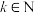 ),并求出X的数学期望.
),并求出X的数学期望.
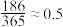 )
)(1)根据以上的调查结果,利用你所学的知识,估计员工对新考勤管理方案满意的概率
 ;
;(2)据核实,以上的300名员工中有15名员工对新考勤管理方案不满意,其中男3人,女12人,试判断是否有97.5%的把握认为与对新考勤管理方案是否满意与性别有关;
参考公式和数据如下:
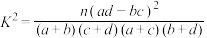 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 7.879 |
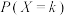 的表达式(其中
的表达式(其中 ,
,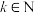 ),并求出X的数学期望.
),并求出X的数学期望.
您最近一年使用:0次
2024-05-11更新
|
590次组卷
|
3卷引用:河北省邢台市第一中学2024届高三下学期二轮复习质量检测数学试题
河北省邢台市第一中学2024届高三下学期二轮复习质量检测数学试题(已下线)第五章 概率统计创新问题 专题六 概率统计中的数学文化 微点5 概率统计中的数学文化综合训练【培优版】重庆市重庆乌江新高考协作体2024届高三下学期模拟监测(三)数学试题
名校
解题方法
7 . 为加强学生体质健康,邢台市第一中学积极组织学生参加课外体育活动.现操场上甲、乙两人玩投篮游戏,每次由其中一人投篮,规则如下:若投中,则继续投篮,若未投中,则换另一人投篮.假设甲每次投篮的命中率均为 ,乙每次投篮的命中率均为
,乙每次投篮的命中率均为 ,由掷两枚硬币的方式确定第一次投篮的人选(一正一反向上是甲投篮,同正或同反是乙投篮),以下选项正确的是( )
,由掷两枚硬币的方式确定第一次投篮的人选(一正一反向上是甲投篮,同正或同反是乙投篮),以下选项正确的是( )
 ,乙每次投篮的命中率均为
,乙每次投篮的命中率均为 ,由掷两枚硬币的方式确定第一次投篮的人选(一正一反向上是甲投篮,同正或同反是乙投篮),以下选项正确的是( )
,由掷两枚硬币的方式确定第一次投篮的人选(一正一反向上是甲投篮,同正或同反是乙投篮),以下选项正确的是( )A.第一次投篮的人是甲的概率为 |
B.第三次投篮的人是乙的概率为 |
C.已知第二次投篮的人是乙的情况下,第一次投篮的人是甲的概率为 |
D.设第n次投篮的人是甲的概率为 ,则 ,则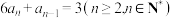 |
您最近一年使用:0次
2024-05-11更新
|
900次组卷
|
3卷引用:河北省邢台市第一中学2024届高三下学期二轮复习质量检测数学试题
名校
解题方法
8 . 已知在 的二项展开式中,第6项为常数项,若在展开式中任取3项,其中有理项的个数为
的二项展开式中,第6项为常数项,若在展开式中任取3项,其中有理项的个数为 ,则
,则 =( )
=( )
 的二项展开式中,第6项为常数项,若在展开式中任取3项,其中有理项的个数为
的二项展开式中,第6项为常数项,若在展开式中任取3项,其中有理项的个数为 ,则
,则 =( )
=( )A. | B.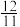 | C. | D. |
您最近一年使用:0次
2024-05-11更新
|
803次组卷
|
2卷引用:河北省邢台市第一中学2024届高三下学期二轮复习质量检测数学试题
名校
9 . 甲企业生产线上生产的零件尺寸的误差 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.
(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量 ,则
,则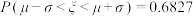 ,
,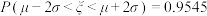 ,
,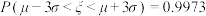 )
)
 服从正态分布
服从正态分布 ,规定
,规定 的零件为优等品,
的零件为优等品, 的零件为合格品.
的零件为合格品.(1)从该生产线上随机抽取100个零件,估计抽到合格品但非优等品的个数(精确到整数);
(2)乙企业拟向甲企业购买这批零件,先对该批零件进行质量抽检,检测的方案是:从这批零件中任取2个作检测,若这2个零件都是优等品,则通过检测;若这2个零件中恰有1个为优等品,1个为合格品但非优等品,则再从这批零件中任取1个作检测,若为优等品,则通过检测;其余情况都不通过检测.求这批零件通过检测时,检测了2个零件的概率(精确到0.01).
(附:若随机变量
 ,则
,则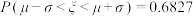 ,
,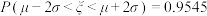 ,
,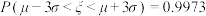 )
)
您最近一年使用:0次
2024-05-07更新
|
1386次组卷
|
5卷引用:专题2 科学研究情境
(已下线)专题2 科学研究情境河北省邢台市南宫中学2023-2024学年高三高考考前定心卷3数学试题(已下线)二项分布与超几何分布、正态分布-一轮复习考点专练(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-1福建省福州市2023-2024学年高三下学期4月末质量检测数学试卷
名校
10 . 在科技飞速发展的今天,人工智能领域迎来革命性的突破.类似于OpenAI的人工智能大模型不仅具有高度智能化、自主化和自适应的特点,它们的学习能力和信息储存能力也远远超越人类,更是拥有强大的语音识别和语言理解能力.某机构分别用 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.
(1)完成下列 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?
(2)将频率视为概率,用 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式及参考数据: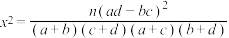 ,
, .
.
 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.(1)完成下列
 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?| 回答正确 | 回答错误 | 合计 | |
 人工智能大模型 人工智能大模型 | |||
 人工智能大模型 人工智能大模型 | |||
| 合计 |
 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式及参考数据:
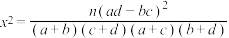 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-03更新
|
976次组卷
|
6卷引用:情境2 最新科技前沿
(已下线)情境2 最新科技前沿(已下线)高二期末模拟卷02(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题贵州省凯里市第一中学2024届高三模拟考试(二模)数学试题湖北省宜昌市远安县第一高级中学2023-2024学年高二下学期5月月考数学试卷