名校
解题方法
1 . 2022年暑假,某社区8名大学生(其中男生5人,女生3人),任选3人参加志愿服务.
(1)设“女生甲被选中”为事件 ,“男生乙被选中”为事件
,“男生乙被选中”为事件 ,求
,求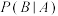 ;
;
(2)设所选3人中男生人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(1)设“女生甲被选中”为事件
 ,“男生乙被选中”为事件
,“男生乙被选中”为事件 ,求
,求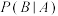 ;
;(2)设所选3人中男生人数为
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2024-09-05更新
|
259次组卷
|
2卷引用:河北省保定部分高中2023届高三第三次模拟数学试题
名校
2 . 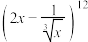 的展开式中常数项为
的展开式中常数项为__________ .
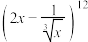 的展开式中常数项为
的展开式中常数项为
您最近一年使用:0次
2024-09-05更新
|
603次组卷
|
5卷引用:河北省保定部分高中2023届高三第三次模拟数学试题
名校
解题方法
3 . 在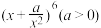 的展开式中,常数项为75,则
的展开式中,常数项为75,则
________ .
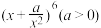 的展开式中,常数项为75,则
的展开式中,常数项为75,则
您最近一年使用:0次
2024-06-17更新
|
406次组卷
|
2卷引用:河北省唐县第一中学2024届高三第三次模拟考试数学试题
4 . 一只口袋装有形状、大小完全相同的3只小球,其中红球、黄球、黑球各1只.现从口袋中先后有放回地取球 次
次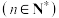 ,且每次取1只球,
,且每次取1只球, 表示
表示 次取球中取到红球的次数,
次取球中取到红球的次数,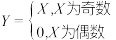 ,则
,则 的数学期望为
的数学期望为______ (用 表示).
表示).
 次
次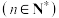 ,且每次取1只球,
,且每次取1只球, 表示
表示 次取球中取到红球的次数,
次取球中取到红球的次数,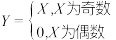 ,则
,则 的数学期望为
的数学期望为 表示).
表示).
您最近一年使用:0次
2024-06-08更新
|
1315次组卷
|
4卷引用:专题9 学科素养与综合问题(填空题14)
5 . 行人闯红灯对自己和他人都可能造成极大的危害,某路口监控设备连续5个月抓拍到行人闯红灯的统计数据如下.
(1)根据表中的数据,求 关于
关于 的回归直线方程
的回归直线方程 ;
;
(2)某组织观察200名行人通过该路口时,发现有4人闯红灯,以这200名行人闯红灯的频率作为通过该路口行人闯红灯的概率,若某段时间内共有10000名行人通过该路口,记闯红灯的行人人数为 ,求
,求 .
.
附:回归直线方程 中,
中, ,
, .
.
月份序号 | 1 | 2 | 3 | 4 | 5 |
闯红灯人数 | 1040 | 980 | 860 | 770 | 700 |
 关于
关于 的回归直线方程
的回归直线方程 ;
;(2)某组织观察200名行人通过该路口时,发现有4人闯红灯,以这200名行人闯红灯的频率作为通过该路口行人闯红灯的概率,若某段时间内共有10000名行人通过该路口,记闯红灯的行人人数为
 ,求
,求 .
.附:回归直线方程
 中,
中, ,
, .
.
您最近一年使用:0次
2024-06-06更新
|
333次组卷
|
2卷引用:2024届河北省保定市九县一中三模联考数学试题
解题方法
6 . 某地下雪导致路面积雪,现安排9名男志愿者,5名女志愿者参与扫雪和铲雪工作,其中3名女志愿者,2名男志愿者参与扫雪工作,其余志愿者参与铲雪工作,则不同的安排方法共有( )
| A.240种 | B.360种 | C.720种 | D.2002种 |
您最近一年使用:0次
2024-06-01更新
|
289次组卷
|
3卷引用:2024届河北省保定市九县一中三模联考数学试题
7 . 在数字通信中,信号是由数字“0”和“1”组成的序列.现连续发射信号n次,每次发射信号“0”和“1”是等可能的.记发射信号1的次数为X.
(1)当 时,求
时,求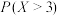 ;
;
(2)已知切比雪夫不等式:对于任一随机变量Y,若其数学期望 和方差
和方差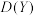 均存在,则对任意正实数a,有
均存在,则对任意正实数a,有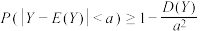 .根据该不等式可以对事件“
.根据该不等式可以对事件“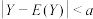 ”的概率作出下限估计.为了至少有96%的把握使发射信号“1”的频率在0.3与0.7之间,试估计信号发射次数n的最小值.
”的概率作出下限估计.为了至少有96%的把握使发射信号“1”的频率在0.3与0.7之间,试估计信号发射次数n的最小值.
(1)当
 时,求
时,求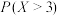 ;
;(2)已知切比雪夫不等式:对于任一随机变量Y,若其数学期望
 和方差
和方差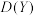 均存在,则对任意正实数a,有
均存在,则对任意正实数a,有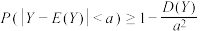 .根据该不等式可以对事件“
.根据该不等式可以对事件“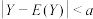 ”的概率作出下限估计.为了至少有96%的把握使发射信号“1”的频率在0.3与0.7之间,试估计信号发射次数n的最小值.
”的概率作出下限估计.为了至少有96%的把握使发射信号“1”的频率在0.3与0.7之间,试估计信号发射次数n的最小值.
您最近一年使用:0次
名校
解题方法
8 . 某火锅店在每周的周一、周三、周五、周日会安排员工跳舞蹈“科目三”,已知某人在一周的七天中,随机选择两天到该店吃火锅,则该人能欣赏到舞蹈“科目三”的概率为( )
A.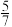 | B.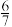 | C. | D.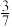 |
您最近一年使用:0次
名校
解题方法
9 . (1)假设变量 与变量
与变量 的
的 对观测数据为
对观测数据为 ,
,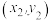 ,
, ,
,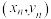 ,两个变量满足一元线性回归模型
,两个变量满足一元线性回归模型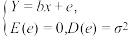 ,请写出参数
,请写出参数 的最小二乘估计;
的最小二乘估计;
(2)为推动新能源汽车产业高质量发展,国家出台了系列政策举措,对新能源汽车产业发展带来了巨大的推动效果.下表是某新能源汽车品牌从2019年到2023年新能源汽车的年销量 (万),其中年份对应的年份代码
(万),其中年份对应的年份代码 为1-5.已知根据散点图和相关系数判断,它们之间具有较强的线性相关关系,可以用线性回归模型描述.
为1-5.已知根据散点图和相关系数判断,它们之间具有较强的线性相关关系,可以用线性回归模型描述.
令变量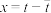 ,
,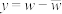 ,则变量
,则变量 与变量
与变量 满足一元线性回归模型
满足一元线性回归模型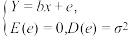 ,利用(1)中结论求
,利用(1)中结论求 关于
关于 的经验回归方程,并预测2025年该品牌新能源汽车的销售量.
的经验回归方程,并预测2025年该品牌新能源汽车的销售量.
 与变量
与变量 的
的 对观测数据为
对观测数据为 ,
,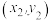 ,
, ,
,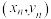 ,两个变量满足一元线性回归模型
,两个变量满足一元线性回归模型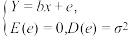 ,请写出参数
,请写出参数 的最小二乘估计;
的最小二乘估计;(2)为推动新能源汽车产业高质量发展,国家出台了系列政策举措,对新能源汽车产业发展带来了巨大的推动效果.下表是某新能源汽车品牌从2019年到2023年新能源汽车的年销量
 (万),其中年份对应的年份代码
(万),其中年份对应的年份代码 为1-5.已知根据散点图和相关系数判断,它们之间具有较强的线性相关关系,可以用线性回归模型描述.
为1-5.已知根据散点图和相关系数判断,它们之间具有较强的线性相关关系,可以用线性回归模型描述.年份代码 | 1 | 2 | 3 | 4 | 5 |
销量 (万) (万) | 4 | 9 | 14 | 18 | 25 |
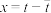 ,
,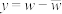 ,则变量
,则变量 与变量
与变量 满足一元线性回归模型
满足一元线性回归模型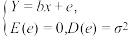 ,利用(1)中结论求
,利用(1)中结论求 关于
关于 的经验回归方程,并预测2025年该品牌新能源汽车的销售量.
的经验回归方程,并预测2025年该品牌新能源汽车的销售量.
您最近一年使用:0次
2024-05-25更新
|
1261次组卷
|
4卷引用:河北省保定市保定名校协作体2024届高三五月适应性考试(三模)数学试题
名校
10 . 如图,一个电路中有 三个电器元件,每个元件正常工作的概率均为
三个电器元件,每个元件正常工作的概率均为 ,这个电路是通路的概率是( )
,这个电路是通路的概率是( )
 三个电器元件,每个元件正常工作的概率均为
三个电器元件,每个元件正常工作的概率均为 ,这个电路是通路的概率是( )
,这个电路是通路的概率是( )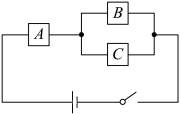
A. | B.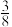 | C.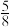 | D. |
您最近一年使用:0次
2024-05-25更新
|
1920次组卷
|
8卷引用:10.2事件的相互独立性【第三课】“上好三节课,做好三套题“高中数学素养晋级之路
(已下线)10.2事件的相互独立性【第三课】“上好三节课,做好三套题“高中数学素养晋级之路河北省保定市保定名校协作体2024届高三五月适应性考试(三模)数学试题(已下线)【高一模块一】难度9小题强化限时晋级练(较难3)(已下线)阶段测7 周测19-周测20(高三一轮提升卷)湖北省武汉市华中师范大学第一附属中学2024届高三五月适应性考试数学试卷广东省华南师范大学附属中学2024届高三下学期5月适应性考试数学试题河北省邢台市四校2023-2024学年高一下学期6月期末联考数学试题贵州省黔西南州金成实验学校2023-2024学年高一下学期6月月考数学试题



