2024高三·全国·专题练习
解题方法
1 . 如图,直四棱柱 被平面
被平面 所截,截面为CDEF,且
所截,截面为CDEF,且 ,
,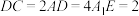 ,
,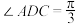 ,平面
,平面 与平面
与平面 所成角的正切值为
所成角的正切值为 .证明:
.证明: .
.
 被平面
被平面 所截,截面为CDEF,且
所截,截面为CDEF,且 ,
,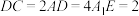 ,
,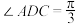 ,平面
,平面 与平面
与平面 所成角的正切值为
所成角的正切值为 .证明:
.证明: .
.
您最近一年使用:0次
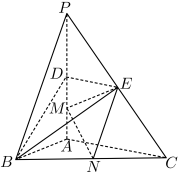
2 . 如图,在三棱锥 中,
中,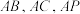 两两互相垂直,
两两互相垂直,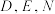 分别为棱
分别为棱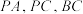 的中点,
的中点, 是线段
是线段 的中点,且
的中点,且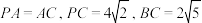
(1)求证: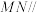 平面
平面 .
.
(2)在棱 上是否存在一点
上是否存在一点 ,使得直线
,使得直线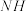 与平面
与平面 所成的角为
所成的角为 ,若存在,求线段
,若存在,求线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 中,
中,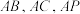 两两互相垂直,
两两互相垂直,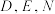 分别为棱
分别为棱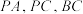 的中点,
的中点, 是线段
是线段 的中点,且
的中点,且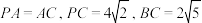

(1)求证:
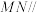 平面
平面 .
.(2)在棱
 上是否存在一点
上是否存在一点 ,使得直线
,使得直线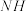 与平面
与平面 所成的角为
所成的角为 ,若存在,求线段
,若存在,求线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
您最近一年使用:0次
解题方法
3 . 一副三角板如图(1),将其中的 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
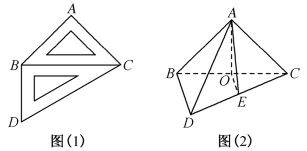
(1)取 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面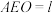 ,求证:
,求证: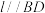 ;
;
(2)证明:平面 ⊥平面
⊥平面 ;
;
(3)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
(1)取
 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面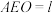 ,求证:
,求证: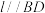 ;
;(2)证明:平面
 ⊥平面
⊥平面 ;
;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
解题方法
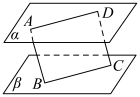
4 . 求证:夹在两个平行平面间的两条平行线段相等.
已知:如图,平面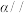 平面
平面 ,AB和DC为夹在
,AB和DC为夹在 ,
, 间的平行线段.求证:
间的平行线段.求证: .
.
已知:如图,平面
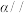 平面
平面 ,AB和DC为夹在
,AB和DC为夹在 ,
, 间的平行线段.求证:
间的平行线段.求证: .
.
您最近一年使用:0次
2023-10-05更新
|
346次组卷
|
3卷引用:湘教版(2019)必修第二册课本例题4.4.1 平面与平面平行
湘教版(2019)必修第二册课本例题4.4.1 平面与平面平行(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】【导学案】4.2平面与平面平行课前预习-北师大版2019必修第二册第六章立体几何初步
2023高二·全国·专题练习
名校
5 . 如图,在四棱锥 中,
中, ,
,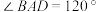 ,
, ,E为PC的中点.
,E为PC的中点.
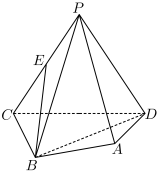
(1)求证: ∥平面PAD;
∥平面PAD;
(2)若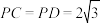 ,平面
,平面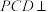 平面ABCD,求二面角
平面ABCD,求二面角 的余弦值.
的余弦值.
 中,
中, ,
,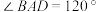 ,
, ,E为PC的中点.
,E为PC的中点.
(1)求证:
 ∥平面PAD;
∥平面PAD;(2)若
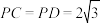 ,平面
,平面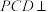 平面ABCD,求二面角
平面ABCD,求二面角 的余弦值.
的余弦值.
您最近一年使用:0次
名校
6 . 如图, ,
, 为圆柱
为圆柱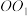 的母线,BC是底面圆O的直径,D,E分别是
的母线,BC是底面圆O的直径,D,E分别是 ,
,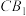 的中点,
的中点, 面
面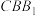 .
.

(1)证明: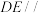 平面ABC;
平面ABC;
(2)若 ,求平面
,求平面 与平面BDC的夹角余弦值.
与平面BDC的夹角余弦值.
 ,
, 为圆柱
为圆柱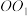 的母线,BC是底面圆O的直径,D,E分别是
的母线,BC是底面圆O的直径,D,E分别是 ,
,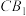 的中点,
的中点, 面
面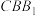 .
.
(1)证明:
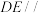 平面ABC;
平面ABC;(2)若
 ,求平面
,求平面 与平面BDC的夹角余弦值.
与平面BDC的夹角余弦值.
您最近一年使用:0次
2023-09-30更新
|
640次组卷
|
4卷引用:浙江省A9协作体2022-2023学年高二上学期期中联考数学试题
名校
解题方法
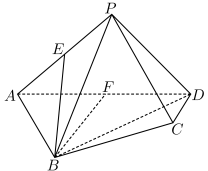
7 . 如图,在四棱锥 中,
中,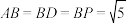 ,
,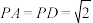 ,
,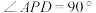 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且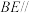 平面
平面 .
. ;
;
(2)已知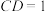 ,求四棱锥
,求四棱锥 的体积.
的体积.
 中,
中,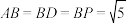 ,
,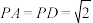 ,
,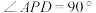 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且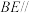 平面
平面 .
.
 ;
;(2)已知
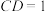 ,求四棱锥
,求四棱锥 的体积.
的体积.
您最近一年使用:0次
2023-09-21更新
|
617次组卷
|
3卷引用:四川省仁寿第一中学校(北校区)2023届高三下学期2月月考文科数学试题
四川省仁寿第一中学校(北校区)2023届高三下学期2月月考文科数学试题(已下线)考点8 平行的判定与性质 2024届高考数学考点总动员【练】云南省昆明市第三中学2023-2024学年高一下学期6月月考数学试卷
解题方法
8 . 如图,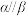 ,
, ,且
,且 ,
, ,
,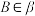 ,
,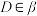 ,求证
,求证 .
.
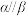 ,
, ,且
,且 ,
, ,
,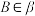 ,
,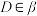 ,求证
,求证 .
.
您最近一年使用:0次
名校
解题方法
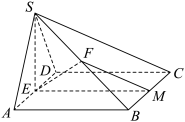
9 . 如图,在四棱锥 中,平面
中,平面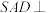 平面
平面 ,
, ,四边形
,四边形 为正方形,
为正方形, 为
为 的中点,
的中点, 为
为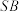 上一点,
上一点, 为
为 上一点,且平面
上一点,且平面 平面
平面 .
.
(1)求证: 为线段
为线段 中点;
中点;
(2)求证:平面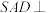 平面
平面 ;
;
(3)在棱 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求
?若存在,求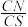 ;若不存在,说明理由.
;若不存在,说明理由.
 中,平面
中,平面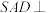 平面
平面 ,
, ,四边形
,四边形 为正方形,
为正方形, 为
为 的中点,
的中点, 为
为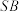 上一点,
上一点, 为
为 上一点,且平面
上一点,且平面 平面
平面 .
.
(1)求证:
 为线段
为线段 中点;
中点;(2)求证:平面
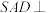 平面
平面 ;
;(3)在棱
 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求
?若存在,求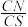 ;若不存在,说明理由.
;若不存在,说明理由.
您最近一年使用:0次
2023-09-06更新
|
731次组卷
|
3卷引用:北京市怀柔区第一中学2023-2024学年高二上学期开学考试数学试题
北京市怀柔区第一中学2023-2024学年高二上学期开学考试数学试题上海市同济大学第二附属中学2023-2024学年高二上学期期中数学试题(已下线)第一章 点线面位置关系 专题二 空间垂直关系的判定与证明 微点6 平面与平面垂直的判定与证明综合训练【基础版】
解题方法
10 . 如图,正方体 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且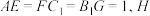 是棱
是棱 上一点.
上一点.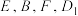 四点共面;
四点共面;
(2)若平面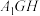 ∥平面
∥平面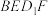 ,求证:
,求证: 为
为 的中点.
的中点.
 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且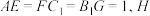 是棱
是棱 上一点.
上一点.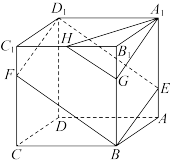
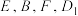 四点共面;
四点共面;(2)若平面
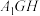 ∥平面
∥平面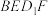 ,求证:
,求证: 为
为 的中点.
的中点.
您最近一年使用:0次
2023-08-06更新
|
808次组卷
|
7卷引用:河北省承德市重点高中2022-2023学年高一下学期5月月考数学试题
河北省承德市重点高中2022-2023学年高一下学期5月月考数学试题河北省沧州市东光县等三县联考2022-2023学年高一下学期4月月考数学试题(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】(已下线)8.5.2平面与平面平行(已下线)6.4.2平面与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)专题13.5空间平面与平面的位置关系-重难点突破及混淆易错规避(苏教版2019必修第二册)(已下线)专题3.5空间直线、平面的平行-重难点突破及混淆易错规避(人教A版2019必修第二册)



