2024高一下·全国·专题练习
解题方法
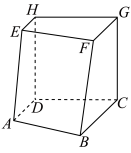
1 . 如图,空间六面体 中,
中,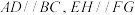 ,平面
,平面
 平面
平面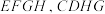 为正方形,求证:
为正方形,求证:

 ;
;
 中,
中,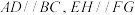 ,平面
,平面
 平面
平面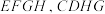 为正方形,求证:
为正方形,求证:

 ;
;
您最近一年使用:0次
2024高一下·全国·专题练习
解题方法
2 . 如图,在四棱锥 中,
中,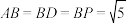 ,
,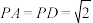 ,
,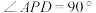 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且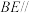 平面
平面 .证明:
.证明: .
.
 中,
中,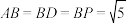 ,
,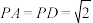 ,
,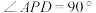 ,
, 、
、 分别是棱
分别是棱 ,
, 的中点,且
的中点,且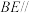 平面
平面 .证明:
.证明: .
.
您最近一年使用:0次
名校
解题方法
3 . 如图,已知四棱锥 中,底面
中,底面 是正方形,
是正方形, 为侧棱
为侧棱 的中点.
的中点.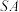 ∥平面
∥平面 ;
;
(2)已知 为棱
为棱 上的点,若
上的点,若 ∥平面
∥平面 ,求证:
,求证: 是
是 的中点.
的中点.
 中,底面
中,底面 是正方形,
是正方形, 为侧棱
为侧棱 的中点.
的中点.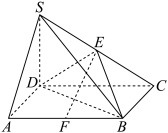
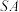 ∥平面
∥平面 ;
;(2)已知
 为棱
为棱 上的点,若
上的点,若 ∥平面
∥平面 ,求证:
,求证: 是
是 的中点.
的中点.
您最近一年使用:0次
2024-06-02更新
|
1156次组卷
|
3卷引用:广东省广州奥林匹克中学2023-2024学年高一下学期期中考试数学试题
广东省广州奥林匹克中学2023-2024学年高一下学期期中考试数学试题(已下线)专题04 立体几何初步(2)-【暑假自学课】(人教A版2019选择性必修第一册)贵州省遵义市第四中学2024-2025学年高二上学期入学质量监测数学试题
名校
4 . 如下左图,矩形 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体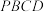 ,如下右图.
,如下右图.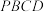 外接球的体积;
外接球的体积;
(2)求证:平面 平面
平面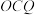 ;
;
(3)若点 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线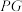 能否平行于面
能否平行于面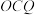 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体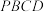 ,如下右图.
,如下右图.
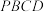 外接球的体积;
外接球的体积;(2)求证:平面
 平面
平面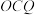 ;
;(3)若点
 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线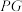 能否平行于面
能否平行于面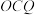 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
您最近一年使用:0次
2024-05-26更新
|
601次组卷
|
4卷引用:安徽省级示范高中培优联盟2023-2024学年高一下学期春季联赛数学试题
安徽省级示范高中培优联盟2023-2024学年高一下学期春季联赛数学试题安徽省亳州市第二完全中学2023-2024学年高一下学期第二次月考(5月)数学试题(已下线)11.4.2 平面与平面垂直-【帮课堂】(人教B版2019必修第四册)广东省湛江市2023-2024学年高一下学期期末调研测试数学试卷
名校
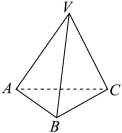
5 . 如图,在三棱锥 中,
中, 和
和 均是边长为4的等边三角形,
均是边长为4的等边三角形,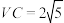 .
. ;
;
(2)已知平面 满足
满足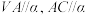 ,且平面
,且平面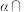 平面
平面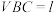 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 和
和 均是边长为4的等边三角形,
均是边长为4的等边三角形,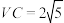 .
.
 ;
;(2)已知平面
 满足
满足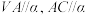 ,且平面
,且平面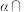 平面
平面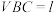 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-05-22更新
|
794次组卷
|
4卷引用:重庆市巴蜀中学校2023-2024学年高一下学期5月期中考试数学试题
重庆市巴蜀中学校2023-2024学年高一下学期5月期中考试数学试题(已下线)暑假作业13 几何法求空间中的距离及空间角-【暑假分层作业】(人教A版2019必修第二册)辽宁省锦州市2023-2024学年高一下学期期末考试数学试卷四川省遂宁中学校高新校区2023-2024学年高一下学期5月月考数学试卷
名校
解题方法
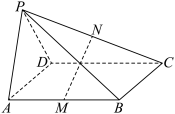
6 . 如图,四棱锥 的侧面
的侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 为矩形,且平面
为矩形,且平面 平面
平面 ,M,N分别为
,M,N分别为 的中点,直线PC与面
的中点,直线PC与面 所成角的正切值为
所成角的正切值为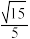 .
.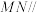 平面
平面 ;
;
(2)证明: .
.
 的侧面
的侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 为矩形,且平面
为矩形,且平面 平面
平面 ,M,N分别为
,M,N分别为 的中点,直线PC与面
的中点,直线PC与面 所成角的正切值为
所成角的正切值为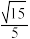 .
.
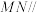 平面
平面 ;
;(2)证明:
 .
.
您最近一年使用:0次
名校
7 . 如下如图,水平桌面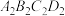 上放置一个透明塑料制成的长方体水槽
上放置一个透明塑料制成的长方体水槽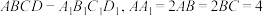 ,水面高度恰为长方体高的一半,在该长方体侧面
,水面高度恰为长方体高的一半,在该长方体侧面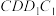 上有一个小孔
上有一个小孔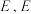 点到
点到 的距离为3.将该长方体水槽绕
的距离为3.将该长方体水槽绕 倾斜(
倾斜( 始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱
始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱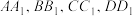 分别相交于点
分别相交于点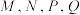 .
.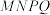 是矩形;
是矩形;
(2)当水恰好流出时,求二面角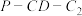 的大小.
的大小.
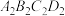 上放置一个透明塑料制成的长方体水槽
上放置一个透明塑料制成的长方体水槽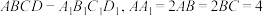 ,水面高度恰为长方体高的一半,在该长方体侧面
,水面高度恰为长方体高的一半,在该长方体侧面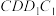 上有一个小孔
上有一个小孔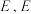 点到
点到 的距离为3.将该长方体水槽绕
的距离为3.将该长方体水槽绕 倾斜(
倾斜( 始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱
始终在桌面上,如下如图所示),此时水恰好流出时,液面与棱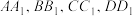 分别相交于点
分别相交于点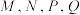 .
.
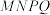 是矩形;
是矩形;(2)当水恰好流出时,求二面角
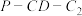 的大小.
的大小.
您最近一年使用:0次
名校
8 . 如图,三棱柱 中,面
中,面 面
面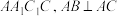 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.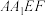 为平行四边形;
为平行四边形;
(2)若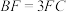 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,面
中,面 面
面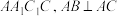 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.
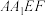 为平行四边形;
为平行四边形;(2)若
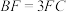 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
解题方法
9 . 在如图所示的直三棱柱 中,
中,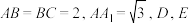 分别是线段
分别是线段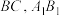 上的动点.
上的动点.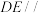 平面
平面 ,求证:
,求证: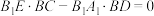 ;
;
(2)若 为正三角形,E是
为正三角形,E是 的中点,求二面角
的中点,求二面角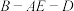 余弦值的最小值.
余弦值的最小值.
 中,
中,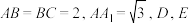 分别是线段
分别是线段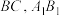 上的动点.
上的动点.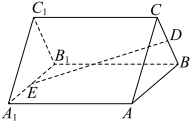
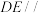 平面
平面 ,求证:
,求证: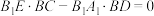 ;
;(2)若
 为正三角形,E是
为正三角形,E是 的中点,求二面角
的中点,求二面角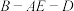 余弦值的最小值.
余弦值的最小值.
您最近一年使用:0次
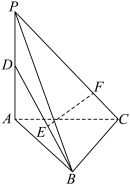
10 . 如图,在四面体 中,
中, 平面
平面 是
是 中点,
中点, 是线段
是线段 上一点(不包含端点),点
上一点(不包含端点),点 在线段
在线段 上,且
上,且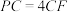 .
. 是
是 中点,求证:
中点,求证: ∥平面
∥平面 ;
;
(2)若 是正三角形,
是正三角形,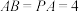 ,且
,且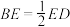 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 中,
中, 平面
平面 是
是 中点,
中点, 是线段
是线段 上一点(不包含端点),点
上一点(不包含端点),点 在线段
在线段 上,且
上,且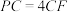 .
.
 是
是 中点,求证:
中点,求证: ∥平面
∥平面 ;
;(2)若
 是正三角形,
是正三角形,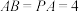 ,且
,且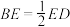 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次



