名校
1 . 设 分别是双曲线
分别是双曲线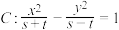 的左、右焦点,且
的左、右焦点,且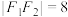 ,则下列结论正确的是( )
,则下列结论正确的是( )
 分别是双曲线
分别是双曲线 的左、右焦点,且
的左、右焦点,且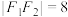 ,则下列结论正确的是( )
,则下列结论正确的是( )A. |
B.t的取值范围是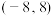 |
C. 到渐近线的距离随着t的增大而减小 到渐近线的距离随着t的增大而减小 |
D.当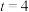 时,C的实轴长是虚轴长的3倍 时,C的实轴长是虚轴长的3倍 |
您最近一年使用:0次
名校
2 . 已知曲线C: ,则( )
,则( )
 ,则( )
,则( )| A.当m=n=2时,C为圆 | B.当m=n=1时,C为抛物线 |
| C.C不可能为椭圆 | D.C可能为双曲线 |
您最近一年使用:0次
2022-03-14更新
|
1064次组卷
|
6卷引用:湖南省长沙市长郡中学2022届高三下学期月考(六)数学试题
(已下线)湖南省长沙市长郡中学2022届高三下学期月考(六)数学试题(已下线)专题39 双曲线及其性质-1江西省上高二中2022-2023学年高二上学期第三次月考(12月)数学试题湖南省百所学校大联考2021-2022学年高二下学期入学考试数学试题重庆市永川区永川北山中学校2022年高二上学期期中数学试题(已下线)专题03 圆锥曲线的方程(1)
名校
3 . 已知二次曲线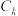 的方程:
的方程: .
.
(1)分别求出方程表示椭圆和双曲线的条件:
(2)若双曲线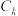 与直线
与直线 有公共点且实轴最长,求双曲线方程:
有公共点且实轴最长,求双曲线方程:
(3) 、
、 为正整数,且
为正整数,且 ,是否存在两条曲线
,是否存在两条曲线 ,其交点
,其交点 与点
与点 满足
满足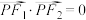 ?若存在,求
?若存在,求 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
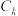 的方程:
的方程: .
.(1)分别求出方程表示椭圆和双曲线的条件:
(2)若双曲线
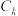 与直线
与直线 有公共点且实轴最长,求双曲线方程:
有公共点且实轴最长,求双曲线方程:(3)
 、
、 为正整数,且
为正整数,且 ,是否存在两条曲线
,是否存在两条曲线 ,其交点
,其交点 与点
与点 满足
满足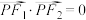 ?若存在,求
?若存在,求 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
2022-11-28更新
|
561次组卷
|
10卷引用:上海市建平中学2023届高三上学期11月月考数学试题
上海市建平中学2023届高三上学期11月月考数学试题上海市嘉定区第二中学2020-2021学年高二上学期第二次月考数学试题上海市闵行(文绮)中学2023届高三下学期开学学情调研数学试题(已下线)高二期末押题02-2020-2021学年高二数学下学期期末专项复习(沪教版)福建省永春第一中学2021-2022学年高二上学期期末考试数学试题上海市宝山中学2021-2022学年高二下学期线上期中数学试题沪教版(2020) 选修第一册 单元训练 第2章 单元测试沪教版(2020) 选修第一册 高效课堂 第二章 2.3 双曲线(3)(已下线)高二上学期期中【压轴60题考点专练】(选修一全部内容)(已下线)第3章 圆锥曲线的方程(基础、典型、易错、新文化、压轴)(2)
名校
4 . 方程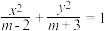 表示双曲线的一个充分不必要条件是( )
表示双曲线的一个充分不必要条件是( )
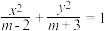 表示双曲线的一个充分不必要条件是( )
表示双曲线的一个充分不必要条件是( )A.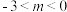 | B.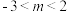 | C.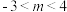 | D.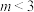 |
您最近一年使用:0次
2022-03-01更新
|
519次组卷
|
5卷引用:广西柳州名校2022-2023学年高三上学期9月月考理科数学试题
广西柳州名校2022-2023学年高三上学期9月月考理科数学试题贵州省毕节市第一中学2021-2022学年高二上学期第二次阶段性考试数学(文)试题贵州省毕节市第一中学2021-2022学年高二上学期第二次阶段性考试数学(理)试题河南省新蔡县第一高级中学2021-2022学年高二下学期3月半月考数学(文科)试题(已下线)1.2 逻辑用语与充分、必要条件(精讲)-【一隅三反】2023年高考数学一轮复习(基础版)(新高考地区专用)
名校
解题方法
5 . 祖暅是南北朝时代伟大的科学家,在数学上有突出贡献.他在五世纪末提出祖暅原理:“密势既同,则积不容异.”其意思是:两个等高的几何体若在所有等高处的水平截面面积相等,则这两个几何体的体积相等.我们称由双曲线 中
中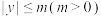 的部分绕其虚轴旋转形成的几何体为双曲线旋转体.如图,双曲线旋转体的下半部分挖去底面直径为2a,高为m的圆柱体后,所得几何体与底面半径为
的部分绕其虚轴旋转形成的几何体为双曲线旋转体.如图,双曲线旋转体的下半部分挖去底面直径为2a,高为m的圆柱体后,所得几何体与底面半径为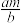 ,高为m的圆锥均放置于平面
,高为m的圆锥均放置于平面 上(几何体底面在
上(几何体底面在 内).与平面
内).与平面 平行且到平面
平行且到平面 距离为
距离为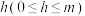 的平面与两几何体的截面面积分别为
的平面与两几何体的截面面积分别为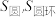 ,可以证明
,可以证明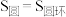 总成立.依据上述原理,
总成立.依据上述原理,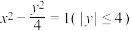 的双曲线旋转体的体积为( )
的双曲线旋转体的体积为( )

 中
中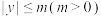 的部分绕其虚轴旋转形成的几何体为双曲线旋转体.如图,双曲线旋转体的下半部分挖去底面直径为2a,高为m的圆柱体后,所得几何体与底面半径为
的部分绕其虚轴旋转形成的几何体为双曲线旋转体.如图,双曲线旋转体的下半部分挖去底面直径为2a,高为m的圆柱体后,所得几何体与底面半径为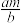 ,高为m的圆锥均放置于平面
,高为m的圆锥均放置于平面 上(几何体底面在
上(几何体底面在 内).与平面
内).与平面 平行且到平面
平行且到平面 距离为
距离为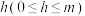 的平面与两几何体的截面面积分别为
的平面与两几何体的截面面积分别为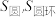 ,可以证明
,可以证明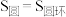 总成立.依据上述原理,
总成立.依据上述原理,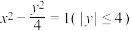 的双曲线旋转体的体积为( )
的双曲线旋转体的体积为( )
A.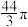 | B. | C.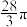 | D.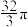 |
您最近一年使用:0次
2022-02-28更新
|
887次组卷
|
5卷引用:安徽省滁州市定远县育才学校2021-2022学年高三下学期第一次月考数学(理)试题
安徽省滁州市定远县育才学校2021-2022学年高三下学期第一次月考数学(理)试题四川省大数据精准教学联盟2022届高三第一次统一检测文科数学试题四川省大数据精准教学联盟2022届高三第一次统一检测理科数学试题(已下线)专题22 祖暅原理(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点2 祖暅原理及球体积辅助体综合训练【培优版】
名校
6 . 方程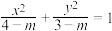 表示的曲线中,可以是( )
表示的曲线中,可以是( )
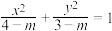 表示的曲线中,可以是( )
表示的曲线中,可以是( )| A.双曲线 | B.椭圆 | C.圆 | D.抛物线 |
您最近一年使用:0次
2022-02-21更新
|
1054次组卷
|
3卷引用:重庆市巴蜀中学2022届高三高考适应性月考(七)数学试题
名校
7 . 已知曲线C方程为: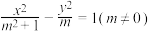 ,则下列结论正确的是( )
,则下列结论正确的是( )
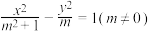 ,则下列结论正确的是( )
,则下列结论正确的是( )A.若 ,则曲线C为双曲线 ,则曲线C为双曲线 | B.若曲线C为椭圆,则其长轴长为 |
| C.曲线C不可能为一个圆 | D.当 时,其渐近线方程为 时,其渐近线方程为 |
您最近一年使用:0次
2022-01-25更新
|
1444次组卷
|
9卷引用:河北省衡水中学2022届高三下学期二调数学试题
河北省衡水中学2022届高三下学期二调数学试题广东省鹤山市鹤华中学2023届高三上学期开学摸底数学试题湖北省部分省级示范高中2021-2022学年高二上学期期末联考数学试题湖北省武汉市十四中联考体2021-2022学年高二上学期期末联考数学试题山东省淄博实验中学2021-2022学年高二下学期开学考试数学试题重庆市复旦中学2021-2022学年高二下学期开学考试数学试题贵州省黔西南布依族苗族自治州2022-2023学年高二上学期期末教学质量监测数学试题四川省资阳市安岳县石羊中学高2023-2024学年高二上学期期中数学(文)试题四川省南充市2023-2024学年高二上学期期末模拟数学试题(四)
名校
解题方法
8 . 双曲线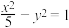 焦点是椭圆C:
焦点是椭圆C: 顶点,且椭圆与双曲线的离心率互为倒数.
顶点,且椭圆与双曲线的离心率互为倒数.
(1)求椭圆C的方程;
(2)设动点 在椭圆C上,且
在椭圆C上,且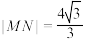 ,记直线
,记直线 在
在 轴上的截距为
轴上的截距为 ,求
,求 的最大值.
的最大值.
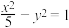 焦点是椭圆C:
焦点是椭圆C: 顶点,且椭圆与双曲线的离心率互为倒数.
顶点,且椭圆与双曲线的离心率互为倒数.(1)求椭圆C的方程;
(2)设动点
 在椭圆C上,且
在椭圆C上,且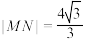 ,记直线
,记直线 在
在 轴上的截距为
轴上的截距为 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2023-12-22更新
|
211次组卷
|
13卷引用:【校级联考】安徽省定远重点中学2019届高三上学期第三次月考数学(文)试题
【校级联考】安徽省定远重点中学2019届高三上学期第三次月考数学(文)试题陕西省汉中市2019-2020学年高三上学期教学质量第一次检测考试数学(理)试题2017届广东省广州市高三4月综合测试(二)数学理试卷河北省衡水中学2018届高三数学(理科)三轮复习系列七-出神入化4辽宁省六校协作体2019-2020学年高三上学期开学考试数学(理)试题辽宁省六校协作体2019-2020学年高三上学期开学考试数学(文)试卷(已下线)2020届高三12月第01期(考点08)(理科)-《新题速递·数学》(已下线)专题10 解析几何中两类曲线相结合问题(第五篇)-备战2020年高考数学大题精做之解答题题型全覆盖辽宁省朝阳市凌源市第二高级中学2020-2021学年高三上学期期中数学试题陕西省汉中市西乡县第一中学2023-2024学年高二上学期第二次(12月)月考数学试题青海省西宁市第十四中学2019-2020学年高二上学期期中数学(理)试题北京师范大学珠海分校附属外国语学校2020-2021学年高二上学期期中考试数学试题(已下线)专题拓展:圆锥曲线的最值与范围问题-【暑假自学课】(人教A版2019选择性必修第一册)
解题方法
9 . 若存在 ,使得当
,使得当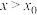 时,恒有
时,恒有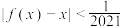 ,则称函数
,则称函数 具有性质P.下列函数中具有性质
具有性质P.下列函数中具有性质 的是( )
的是( )
 ,使得当
,使得当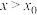 时,恒有
时,恒有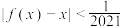 ,则称函数
,则称函数 具有性质P.下列函数中具有性质
具有性质P.下列函数中具有性质 的是( )
的是( )A. | B.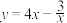 |
C. | D.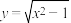 |
您最近一年使用:0次
名校
10 . 若方程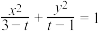 所表示的曲线为
所表示的曲线为 ,则下面四个命题中正确的是( )
,则下面四个命题中正确的是( )
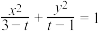 所表示的曲线为
所表示的曲线为 ,则下面四个命题中正确的是( )
,则下面四个命题中正确的是( )A.若 为椭圆,则 为椭圆,则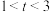 | B.若 为双曲线,则 为双曲线,则 或 或 |
C.曲线 可能是圆 可能是圆 | D.若 为椭圆,且长轴在 为椭圆,且长轴在 轴上,则 轴上,则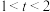 |
您最近一年使用:0次
2022-05-20更新
|
4333次组卷
|
23卷引用:广东省梅州市五华县2023届高三上学期12月质检数学试题
广东省梅州市五华县2023届高三上学期12月质检数学试题广东省佛山市南海区南海艺术高级中学2022届高三下学期第四次综合测试数学试题(已下线)第06讲 双曲线 (精讲)-1广西玉林市博白县第四中学(博白县中学书香校区)2022-2023学年高二上学期12月段考数学试题广东省揭阳市惠来县第一中学2022-2023学年高二上学期第二次阶段考试(12月)数学试题(已下线)模块六 平面解析几何-1陕西省西安市西咸新区泾河新城第一中学2023-2024学年高二上学期阶段质量检测(二)数学试题江苏省张家港市暨阳高级中学2023-2024学年高二上学期12月自主学习能力测试数学试卷广东省东莞市万江中学2023-2024学年高二上学期第二次月考(1月)数学试题山东省滨州市2020-2021学年高二上学期期末数学试题山东省惠民县第二中学致远高中部2020-2021学年度高二上学期期末考试数学试题安徽省合肥市第一中学2021-2022学年高二上学期期末数学试题重庆市巫山县官渡中学2021-2022学年高二下学期期末数学试题福建师范大学附属中学2021-2022学年高二上学期期末考试数学试题黑龙江省哈尔滨市尚志中学2022-2023学年高二上学期期中考试数学试题黑龙江省伊春市伊美区第二中学2021-2022学年高二上学期期末数学试题(已下线)专题3.2 双曲线(4类必考点)-2022-2023学年高二数学必考点分类集训系列(人教A版2019选择性必修第一册)(已下线)第17讲 双曲线10大基础题型总结(1)(已下线)专题3.8 双曲线的标准方程和性质-重难点题型检测-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)云南省元谋县第一中学2022-2023学年高二下学期数学期末模拟(六)试题3.2.1 双曲线及其标准方程练习(已下线)2.6.1 双曲线的标准方程(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第一册)专题09双曲线问题(选择填空题)



