北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
北京
高一
阶段练习
2024-07-09
505次
整体难度:
容易
考查范围:
平面向量、三角函数与解三角形、集合与常用逻辑用语、复数
北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
北京
高一
阶段练习
2024-07-09
505次
整体难度:
容易
考查范围:
平面向量、三角函数与解三角形、集合与常用逻辑用语、复数
一、单选题 添加题型下试题
单选题
|
容易(0.94)
名校
解题方法
1. 已知向量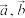 满足
满足 ,则
,则 ( )
( )
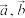 满足
满足 ,则
,则 ( )
( )A. | B.0 | C.5 | D.7 |
【知识点】 平面向量线性运算的坐标表示解读 数量积的坐标表示解读
您最近一年使用:0次
2023-11-02更新
|
1263次组卷
|
4卷引用:北京市海淀区2024届高三上学期期中练习数学试题
北京市海淀区2024届高三上学期期中练习数学试题(已下线)第一篇 “必拿”选择前5填空前2 专题12 平面向量的基本运算【练】北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题广东省广州市清华附中湾区学校2023~2024学年高一下学期期中考试数学试卷
单选题
|
容易(0.94)
名校
2.  是圆心为
是圆心为 的单位圆上两个动点,当
的单位圆上两个动点,当 面积最大时,则下列判断错误的是( )
面积最大时,则下列判断错误的是( )
 是圆心为
是圆心为 的单位圆上两个动点,当
的单位圆上两个动点,当 面积最大时,则下列判断错误的是( )
面积最大时,则下列判断错误的是( )A. | B.弧 的长为 的长为 |
C.扇形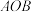 的面积为 的面积为 | D. 等边三角形 等边三角形 |
您最近一年使用:0次
单选题
|
较易(0.85)
名校
3. 如图,圆 的半径为
的半径为 ,
, 是圆上的定点,
是圆上的定点, 是圆上的动点,角
是圆上的动点,角 的始边为射线
的始边为射线 ,终边为射线
,终边为射线 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,将点
,将点 到直线
到直线 的距离表示为
的距离表示为 的函数
的函数 ,则
,则 在
在 上的图像大致为( )
上的图像大致为( )
 的半径为
的半径为 ,
, 是圆上的定点,
是圆上的定点, 是圆上的动点,角
是圆上的动点,角 的始边为射线
的始边为射线 ,终边为射线
,终边为射线 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,将点
,将点 到直线
到直线 的距离表示为
的距离表示为 的函数
的函数 ,则
,则 在
在 上的图像大致为( )
上的图像大致为( )
A. | B.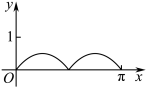 |
C.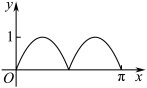 | D. |
您最近一年使用:0次
2020-09-12更新
|
2643次组卷
|
26卷引用:2015-2016学年河北省武邑中学高一上周考数学试卷
2015-2016学年河北省武邑中学高一上周考数学试卷福建省2016届高三毕业班总复习(三角函数)单元过关平行性测试卷(理科)数学试题贵州省遵义航天高级中学2016-2017学年高一下学期第三次月考数学试题辽宁省凌源二中2018-2019学年高一下学期期末数学试题山东省菏泽市2018-2019学年高一下学期期末数学试题上海市曹杨二中2018-2019学年高一下学期期中数学试题(已下线)3.3 正弦定理 余弦定理与解三角形 [理]-《备战2020年高考精选考点专项突破题集》(已下线)3.3 正弦定理 余弦定理与解三角形 [文] -《备战2020年高考精选考点专项突破题集》山东省菏泽市东明县第一中学2018-2019学年高一下学期期末数学试题(已下线)题型05 三角函数求解析式-2020届秒杀高考数学题型之三角2020届上海市奉贤区高三二模数学试题(已下线)专题13 三角函数的综合应用-十年(2011-2020)高考真题数学分项(二)广东省韶关一中2017-2018学年高一上学期期末数学试题(已下线)5.7+三角函数的应用-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)(已下线)第7节+三角函数的应用-2020-2021学年高一数学上学期课时同步练(新人教A版必修第一册)(已下线)考点03 三角函数与解三角形-2021年高考数学【热点·重点·难点】专练(上海专用)江西省赣州市会昌中学2020-2021学年高一上学期第二次月考数学试题江苏省泰州市姜堰第二中学2020-2021学年高三上学期学情检测一数学试题北京市育英学校2022届高三10月月考数学试题(已下线)专题07函数的图像、函数与方程 -2022年高三毕业班数学常考点归纳与变式演练(文理通用)福建省莆田第一中学2022届高三10月月考数学试题(已下线)易错点03 函数概念与基本函数-备战2022年高考数学考试易错题(全国通用)(已下线)考向09 函数的图像(重点)(已下线)专题02 函数-2(已下线)专题02 函数选择题(理科)-3北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
单选题
|
适中(0.65)
名校
4. 将函数 的图象向左平移
的图象向左平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数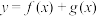 的最大值为
的最大值为 ,则
,则 的值不可能为( )
的值不可能为( )
 的图象向左平移
的图象向左平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数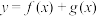 的最大值为
的最大值为 ,则
,则 的值不可能为( )
的值不可能为( )A. | B. |
C. | D.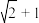 |
您最近一年使用:0次
2023-11-02更新
|
843次组卷
|
4卷引用:北京市丰台区2024届高三上学期期中练习数学试题
北京市丰台区2024届高三上学期期中练习数学试题(已下线)模块四 题型突破篇 小题满分挑战练(2)2024届河北省衡水市部分高中高三一模数学试题北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
单选题
|
适中(0.65)
名校
解题方法
5. “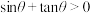 ”是“
”是“ 为第一或第三象限角”的( )
为第一或第三象限角”的( )
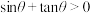 ”是“
”是“ 为第一或第三象限角”的( )
为第一或第三象限角”的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2023-11-02更新
|
1672次组卷
|
12卷引用:北京市海淀区2024届高三上学期期中练习数学试题
北京市海淀区2024届高三上学期期中练习数学试题北京市第一六一中学2024届高三上学期12月阶段测试数学试题(已下线)第五章:三角函数章末重点题型复习(1)-同步精品课堂(人教A版2019必修第一册)(已下线)专题5-1 弧度制与三角函数(2) - 【巅峰课堂】题型归纳与培优练(已下线)第7章:三角函数章末重点题型复习(1)-【题型分类归纳】(苏教版2019必修第一册)(已下线)第7章:三角函数章末重点题型复习-【题型分类归纳】(苏教版2019必修第一册)(已下线)第五章:三角函数章末重点题型复习(1)-【题型分类归纳】(人教A版2019必修第一册)北京市中关村中学2023-2024学年高一下学期期中调研数学试题北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题北京市第二中学2024-2025学年高三上学期10月月考数学试卷(已下线)考点32 同角三角函数基本关系式 --高考数学100个黄金考点(2025届)【讲】北京市西城区北京师范大学附属实验中学2025届高三上学期第二次测试数学试卷
单选题
|
适中(0.65)
名校
解题方法
6. 关于函数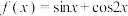 ,给出下列三个命题:
,给出下列三个命题:
① 是周期函数;②曲线
是周期函数;②曲线 关于直线
关于直线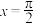 对称;
对称;
③ 在区间
在区间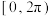 上恰有3个零点.④
上恰有3个零点.④ 最小值为-2
最小值为-2
其中真命题的个数为( )
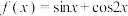 ,给出下列三个命题:
,给出下列三个命题:①
 是周期函数;②曲线
是周期函数;②曲线 关于直线
关于直线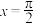 对称;
对称;③
 在区间
在区间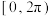 上恰有3个零点.④
上恰有3个零点.④ 最小值为-2
最小值为-2其中真命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
单选题
|
较易(0.85)
名校
解题方法
7. 在 中,
中,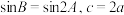 ,则( )
,则( )
 中,
中,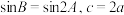 ,则( )
,则( )A. 为直角 为直角 | B. 为钝角 为钝角 | C.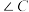 为直角 为直角 | D.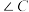 为钝角 为钝角 |
您最近一年使用:0次
2023-11-02更新
|
1146次组卷
|
6卷引用:北京市海淀区2024届高三上学期期中练习数学试题
北京市海淀区2024届高三上学期期中练习数学试题(已下线)第三篇 努力 “争取”考点 专题3 解三角形【讲】(已下线)专题06 解三角形及应用(3大易错点分析+解题模板+举一反三+易错题通关)(已下线)第11讲 6.4.3 第2课时 正弦定理 (1)-【帮课堂】(人教A版2019必修第二册)(已下线)专题09 余弦定理、正弦定理的应用-《重难点题型·高分突破》(人教A版2019必修第二册)北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
单选题
|
较易(0.85)
名校
8. 在 中,
中,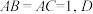 是
是 的中点,则
的中点,则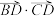 的取值范围是
的取值范围是
 中,
中,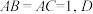 是
是 的中点,则
的中点,则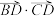 的取值范围是
的取值范围是A. | B. | C.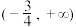 | D.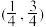 |
您最近一年使用:0次
2018-01-19更新
|
1034次组卷
|
6卷引用:北京市海淀区2018届高三第一学期期末文科数学试题
单选题
|
适中(0.65)
名校
解题方法
9. 已知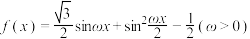 ,则下列说法错误的是( )
,则下列说法错误的是( )
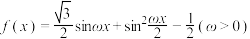 ,则下列说法错误的是( )
,则下列说法错误的是( )A.若 在 在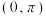 内单调,则 内单调,则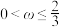 |
B.若 在 在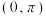 内无零点,则 内无零点,则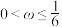 |
C.若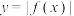 的最小正周期为 的最小正周期为 ,则 ,则 |
D.若 时,直线 时,直线 是函数 是函数 图象的一条对称轴 图象的一条对称轴 |
【知识点】 三角函数图象的综合应用解读 三角恒等变换的化简问题解读
您最近一年使用:0次
2021-01-21更新
|
347次组卷
|
3卷引用:北京市中国人民大学附属中学2021届高三1月期末模拟统一练习数学试题
单选题
|
较易(0.85)
名校
您最近一年使用:0次
2020-11-03更新
|
587次组卷
|
8卷引用:北京市八一学校2021届高三年级十月月考数学试题
北京市八一学校2021届高三年级十月月考数学试题(已下线)专题07 平面向量——2020年高考数学母题题源解密(山东、海南专版)北京市第四十三中学2022届高三上学期期中考试数学试题(已下线)专题4-3 正余弦定理与解三角形小题归类2-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)北京市朝阳区2019-2020学年高三上学期期中数学试题(已下线)北京市西城区2022届高三二模数学试题变式题6-10北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题北京市第八十中学2025届高三上学期10月考试数学试题
二、填空题 添加题型下试题
填空题-单空题
|
较易(0.85)
名校
您最近一年使用:0次
填空题-单空题
|
容易(0.94)
名校
13. 在 中,
中,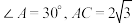 ,满足此条件
,满足此条件 有两解,则
有两解,则 边长度的取值范围为
边长度的取值范围为__________ .
 中,
中,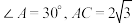 ,满足此条件
,满足此条件 有两解,则
有两解,则 边长度的取值范围为
边长度的取值范围为【知识点】 正弦定理判定三角形解的个数解读
您最近一年使用:0次
2024-07-07更新
|
220次组卷
|
3卷引用:北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题(已下线)数学(北京专用)-新高二上学期数学开学摸底考试卷湖南省娄底市涟源市部分学校2024-2025学年高二上学期开学考试数学试题
填空题-单空题
|
较易(0.85)
名校
解题方法
14. 已知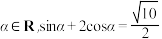 ,则
,则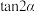 =
=___________________
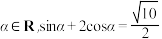 ,则
,则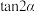 =
=
您最近一年使用:0次
2017-05-17更新
|
466次组卷
|
12卷引用:2014届安徽省淮南二中高三上学期第三次月考文科数学试卷
(已下线)2014届安徽省淮南二中高三上学期第三次月考文科数学试卷(已下线)2014届安徽池州第一中学高三上学期第三次月考文科数学试卷(已下线)2014年高考数学(文)二轮复习专题提升训练江苏专用7练习卷内蒙古集宁一中2017届高三上学期第一次月考数学(文)试题山西省太原市第五中学2019届高三下学期阶段性考试(5月)数学(文)试题安徽省黄山市屯溪第一中学2019-2020学年高一下学期入学考试数学试题沪教版(上海) 高三年级 新高考辅导与训练 第二部分 走近高考 第三章 三角高考题选上海市黄浦区格致中学2020-2021学年高一下学期3月月考数学试题山西省太原市第五中学2019届高三下学期阶段性考试(5月)数学(理)试题上海市南洋中学2021-2022学年高一下学期第一次月考数学试题(已下线)【第一课】5.5.2简单的三角恒等变换北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
填空题-单空题
|
适中(0.65)
名校
解题方法
15. 设 的内角
的内角 所对边的长分别为
所对边的长分别为
①若 ,则
,则 ;
;
②若 .则
.则 ;
;
③若 ,则
,则 一定为等腰直角三角形;
一定为等腰直角三角形;
④若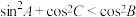 ,则
,则 一定为钝角三角形;
一定为钝角三角形;
⑤若 ,则
,则 一定为锐角三角形.
一定为锐角三角形.
则上述命题中正确的是__________ .(写出所有正确命题的编号)
 的内角
的内角 所对边的长分别为
所对边的长分别为
①若
 ,则
,则 ;
;②若
 .则
.则 ;
;③若
 ,则
,则 一定为等腰直角三角形;
一定为等腰直角三角形;④若
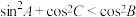 ,则
,则 一定为钝角三角形;
一定为钝角三角形;⑤若
 ,则
,则 一定为锐角三角形.
一定为锐角三角形.则上述命题中正确的是
您最近一年使用:0次
三、解答题 添加题型下试题
解答题-问答题
|
适中(0.65)
名校
解题方法
16. 在平面直角坐标系中, 为原点,
为原点,
(1) 在直线
在直线 上的投影是
上的投影是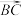 ,求
,求
(2)若四边形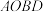 是以
是以 为底的直角梯形,求点
为底的直角梯形,求点
 为原点,
为原点,
(1)
 在直线
在直线 上的投影是
上的投影是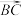 ,求
,求
(2)若四边形
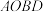 是以
是以 为底的直角梯形,求点
为底的直角梯形,求点
【知识点】 由向量共线(平行)求参数解读 利用向量垂直求参数 已知向量垂直求参数
您最近一年使用:0次
解答题-问答题
|
适中(0.65)
名校
解题方法
17. 在 中,
中,
(1)求 ;
;
(2)若 为
为 边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使
边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使 存在且唯一确定,求
存在且唯一确定,求 的面积.
的面积.
条件①: ;
;
条件②: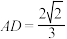 ;
;
条件③: 的周长为
的周长为 .
.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
 中,
中,
(1)求
 ;
;(2)若
 为
为 边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使
边上一点,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使 存在且唯一确定,求
存在且唯一确定,求 的面积.
的面积.条件①:
 ;
;条件②:
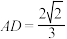 ;
;条件③:
 的周长为
的周长为 .
.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
您最近一年使用:0次
2024-01-19更新
|
942次组卷
|
5卷引用:北京市东城区2024届高三上学期期末统一检测数学试题
北京市东城区2024届高三上学期期末统一检测数学试题(已下线)考点15 正弦定理、余弦定理的综合应用 --2024届高考数学考点总动员【讲】(已下线)2024年高考数学二轮复习测试卷(北京专用)北京市第一六六中学2023-2024学年高一下学期月考(期末模拟)数学试卷北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
解答题-问答题
|
适中(0.65)
18. 已知函数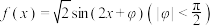 的图象上所有点向右平移
的图象上所有点向右平移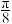 个单位长度,所得函数图象关于原点对称.
个单位长度,所得函数图象关于原点对称.
(1)求 的值;
的值;
(2)设 ,若
,若 在区间
在区间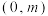 上有且只有一个零点,求
上有且只有一个零点,求 的取值范围.
的取值范围.
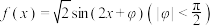 的图象上所有点向右平移
的图象上所有点向右平移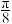 个单位长度,所得函数图象关于原点对称.
个单位长度,所得函数图象关于原点对称.(1)求
 的值;
的值;(2)设
 ,若
,若 在区间
在区间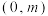 上有且只有一个零点,求
上有且只有一个零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-01-17更新
|
1151次组卷
|
4卷引用:北京市房山区2024届高三上学期期末数学试题
北京市房山区2024届高三上学期期末数学试题福建师范大学附属中学2023-2024学年高一上学期期末考试数学试题(已下线)7.3.2 正弦型函数的性质与图象(2)-【帮课堂】(人教B版2019必修第三册)北京市中国人民大学附属中学2023-2024学年高一下学期统练四数学试题
试卷分析
导出
整体难度:适中
考查范围:平面向量、三角函数与解三角形、集合与常用逻辑用语、复数
试卷题型(共 18题)
题型
数量
单选题
10
填空题
5
解答题
3
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 平面向量线性运算的坐标表示 数量积的坐标表示 | |
| 2 | 0.94 | 弧长的有关计算 扇形面积的有关计算 三角形面积公式及其应用 | |
| 3 | 0.85 | 识别三角函数的图象(含正、余弦,正切) 几何中的三角函数模型 | |
| 4 | 0.65 | 结合三角函数的图象变换求三角函数的性质 用和、差角的正弦公式化简、求值 辅助角公式 | |
| 5 | 0.65 | 探求命题为真的充要条件 由三角函数式的符号确定角的范围或象限 三角函数的化简、求值——同角三角函数基本关系 | |
| 6 | 0.65 | 求cosx(型)函数的对称轴及对称中心 二倍角的余弦公式 求含sinx(型)的二次式的最值 | |
| 7 | 0.85 | 正弦定理边角互化的应用 余弦定理解三角形 正、余弦定理判定三角形形状 | |
| 8 | 0.85 | 平面向量的线性运算 用基底表示向量 平面向量基本定理的应用 用定义求向量的数量积 | |
| 9 | 0.65 | 三角函数图象的综合应用 三角恒等变换的化简问题 | |
| 10 | 0.85 | 数量积的坐标表示 向量模的坐标表示 | |
| 二、填空题 | |||
| 11 | 0.85 | 求复数的实部与虚部 复数的除法运算 | 单空题 |
| 12 | 0.85 | 余弦定理解三角形 | 单空题 |
| 13 | 0.94 | 正弦定理判定三角形解的个数 | 单空题 |
| 14 | 0.85 | 正、余弦齐次式的计算 三角函数的化简、求值——同角三角函数基本关系 二倍角的正切公式 | 单空题 |
| 15 | 0.65 | 逆用和、差角的正切公式化简、求值 二倍角的正弦公式 正弦定理及辨析 余弦定理解三角形 | 单空题 |
| 三、解答题 | |||
| 16 | 0.65 | 由向量共线(平行)求参数 利用向量垂直求参数 已知向量垂直求参数 | 问答题 |
| 17 | 0.65 | 正弦定理解三角形 三角形面积公式及其应用 余弦定理解三角形 | 问答题 |
| 18 | 0.65 | 正弦函数图象的应用 由正弦(型)函数的奇偶性求参数 结合三角函数的图象变换求三角函数的性质 三角恒等变换的化简问题 | 问答题 |

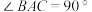 ,
, ,点
,点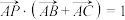 ,则
,则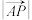 的取值范围是(
的取值范围是(
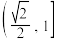
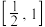
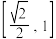
 .
. 的虚部
的虚部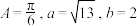 ,则
,则