1 . 已知函数 ,
,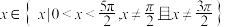 ,有两个零点
,有两个零点 ,则下列结论正确的是( )
,则下列结论正确的是( )
 ,
,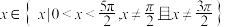 ,有两个零点
,有两个零点 ,则下列结论正确的是( )
,则下列结论正确的是( )A.当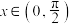 时, 时,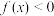 | B.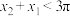 |
C.若 ,则 ,则 | D.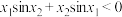 |
您最近半年使用:0次
解题方法
2 . 已知函数 的定义域为
的定义域为 ,若存在常数
,若存在常数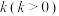 ,使得对
,使得对 内的任意
内的任意 ,
,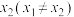 ,都有
,都有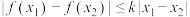 ,则称
,则称 是“
是“ -利普希兹条件函数”.
-利普希兹条件函数”.
(1)判断函数 ,
, 是否为“2-利普希兹条件函数”,并说明理由;
是否为“2-利普希兹条件函数”,并说明理由;
(2)若函数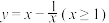 是“
是“ -利普希兹条件函数”,求
-利普希兹条件函数”,求 的最小值;
的最小值;
(3)设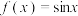 ,若
,若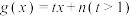 是“2024-利普希兹条件函数”,且
是“2024-利普希兹条件函数”,且 的零点
的零点 也是
也是 的零点,
的零点, . 证明:方程
. 证明:方程 在区间
在区间 上有解.
上有解.
 的定义域为
的定义域为 ,若存在常数
,若存在常数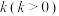 ,使得对
,使得对 内的任意
内的任意 ,
,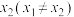 ,都有
,都有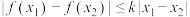 ,则称
,则称 是“
是“ -利普希兹条件函数”.
-利普希兹条件函数”.(1)判断函数
 ,
, 是否为“2-利普希兹条件函数”,并说明理由;
是否为“2-利普希兹条件函数”,并说明理由;(2)若函数
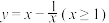 是“
是“ -利普希兹条件函数”,求
-利普希兹条件函数”,求 的最小值;
的最小值;(3)设
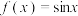 ,若
,若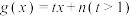 是“2024-利普希兹条件函数”,且
是“2024-利普希兹条件函数”,且 的零点
的零点 也是
也是 的零点,
的零点, . 证明:方程
. 证明:方程 在区间
在区间 上有解.
上有解.
您最近半年使用:0次
3 . 在 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求 ;
;
(2)若 是
是 边上一点,且
边上一点,且 ,设边
,设边 上的高为
上的高为 ,求
,求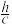 .
.
 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.(1)求
 ;
;(2)若
 是
是 边上一点,且
边上一点,且 ,设边
,设边 上的高为
上的高为 ,求
,求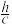 .
.
您最近半年使用:0次
4 . 函数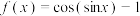 在区间
在区间 上有两个零点,则实数
上有两个零点,则实数 的取值范围为
的取值范围为________ .
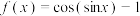 在区间
在区间 上有两个零点,则实数
上有两个零点,则实数 的取值范围为
的取值范围为
您最近半年使用:0次
2023-12-08更新
|
976次组卷
|
4卷引用:湖北省黄冈市部分普通高中2024届高三上学期阶段性教学质量监测数学试题
湖北省黄冈市部分普通高中2024届高三上学期阶段性教学质量监测数学试题广东省惠州市第一中学2023-2024学年高一上学期12月阶段考试数学试题(已下线)专题08 三角函数的图象与性质(2)-【寒假自学课】(苏教版2019)(已下线)专题05 三角函数4-2024年高一数学寒假作业单元合订本
2023·全国·模拟预测
解题方法
5 . 记 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 .
.
(1)判断 与
与 的等量关系,并证明.
的等量关系,并证明.
(2)若 ,求
,求 周长的取值范围.
周长的取值范围.
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 .
.(1)判断
 与
与 的等量关系,并证明.
的等量关系,并证明.(2)若
 ,求
,求 周长的取值范围.
周长的取值范围.
您最近半年使用:0次
解题方法
6 .  的周长为20,面积为
的周长为20,面积为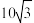 ,
, ,则边
,则边 的长是
的长是__________
 的周长为20,面积为
的周长为20,面积为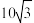 ,
, ,则边
,则边 的长是
的长是
您最近半年使用:0次
名校
解题方法
7 . 若函数 的一个零点为
的一个零点为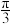 ,则
,则
__________ .
 的一个零点为
的一个零点为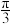 ,则
,则
您最近半年使用:0次
2023-10-19更新
|
117次组卷
|
2卷引用:广东省深圳市云顶学校2024届高三上学期8月质量检测数学试题
名校
解题方法
8 . 在 中,内角
中,内角 ,
, ,
, 所对应的边分别为
所对应的边分别为 ,
, ,
, ,若
,若 ,且
,且 ,则
,则 的面积为( )
的面积为( )
 中,内角
中,内角 ,
, ,
, 所对应的边分别为
所对应的边分别为 ,
, ,
, ,若
,若 ,且
,且 ,则
,则 的面积为( )
的面积为( )A.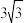 | B. | C.3 | D.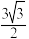 |
您最近半年使用:0次
2023-10-13更新
|
1268次组卷
|
89卷引用:2015-2016学年山东省枣庄市三中高二10月学情调查数学试卷
2015-2016学年山东省枣庄市三中高二10月学情调查数学试卷2015-2016学年江西玉山一中高一下第三次考试理科数学卷2016届江西省上高二中高三全真模拟文科数学试卷2015-2016学年陕西西藏民族学院附中高一下期末数学试卷2017届广西南宁二中等校高三8月联考数学(文)试卷2017届广西南宁二中等高三8月联考数学(文)试卷2017届广西河池课改联盟高三上联考二试数学(文)试卷2016-2017学年广东湛江一中高二上大考一数学(文)试卷2016-2017学年山东省淄博市临淄中学高二上学期期末考试数学(理)试卷2016-2017学年山东省淄博市临淄中学高二上学期期末考试数学(文)试卷甘肃省高台县第一中学2016-2017学年高一下学期期中考试数学试题甘肃省通渭县第二中学2018届高三上学期第一次月考数学(理)试题河南省林州市第一中学2017-2018学年高二10月月考数学试题山东省临沂市第一中学2017-2018学年高二年级上学期期中考试数学试题山东省潍坊市第七中学2017-2018学年高二上学期期中考试数学试题(已下线)《考前20天终极攻略》5月21日 解三角形【理科】(已下线)《考前20天终极攻略》5月21日 解三角形【文科】(已下线)《高频考点解密》—解密09 正、余弦定理及解三角形(已下线)解密08 正、余弦定理及解三角形-备战2018年高考文科数学之高频考点解密【全国百强校】广东省深圳外国语学校2017-2018学年高二下学期第二学段考试数学(理)试题人教A版 全能练习 全能练习 不等式 模块结业测评(二)(已下线)2019高考热点题型和提分秘籍 【理数】专题17 正弦定理和余弦定理及解三角形 (教学案)(已下线)2019高考热点题型和提分秘籍 【文数】专题17 正弦定理和余弦定理及解三角形 (教学案)【全国百强校】云南省玉溪第一中学2018-2019学年高二上学期第二次月考数学(理)试题智能测评与辅导[理]-解三角形(已下线)2019年9月1日《每日一题》人教必修5 —— 每周一测人教A版 成长计划 必修5 第一章正弦定理和余弦定理 高考链接陕西省榆林市第二中学2019-2020学年高二上学期期中数学(理)试题山西省朔州市怀仁一中2018-2019学年高一下学期第四次月考数学(文)试题内蒙古包头市稀土高新区二中2018-2019学年高一下学期第一次月考数学(文)试题黑龙江省哈尔滨师范大学附中2018-2019学年高一下学期开学考试数学试题陕西省渭滨中学2019-2020学年高二上学期期中数学(理)试题陕西省渭滨中学2019-2020学年高二上学期期中数学(文)试题山东省菏泽市2018-2019学年高一下学期期末考试数学试题(B)2020届宁夏银川市第二中学高三上学期统练二数学(理科)试题2020届黑龙江哈尔滨市第三十二中学高三上学期期末数学(文)试题吉林省白城市第四中学2019-2020学年下学期高一网上阶段检测试卷数学试题2020届陕西省榆林市第二中学高三下学期3月月考数学(理)试题黑龙江省哈尔滨三中2017-2018学年高三上学期期中考试理科数学试题天津市第七中学2019~2020学年高一下学期期中考试数学试题云南省云天化中学2019-2020学年高二下学期开学考试数学(理科)试题云南省云天化中学2019-2020学年高二下学期开学考试数学(文科)试题重庆市云阳江口中学校2019-2020学年高三下学期第一次月考数学(理)试题重庆市第八中学2019-2020学年高一下学期第一次月考数学试题四川省攀枝花市第十五中学2019-2020学年高一下学期期中考试数学(理科)试题四川省攀枝花市第十五中学2019-2020学年高一下学期期中考试数学(文)试卷(已下线)1.1.2余弦定理(1) -2020-2021学年高二 数学课时同步练(人教A版必修5)(已下线)专题14 解三角形-十年(2011-2020)高考真题数学分项湖北省黄冈市黄梅国际育才高级中学2018-2019学年高一下学期3月月考数学试题山西省朔州市怀仁县大地学校2019-2020学年高一下学期6月月考数学试题安徽省马鞍山市和县第二中学2020-2021学年高一上学期期中联考数学(理)试题(已下线)考点30 正弦定理与余弦定理(2)-备战2021年高考数学经典小题考前必刷(新高考地区专用)(已下线)【新东方】高中数学20210527-010【2021】【高二下】河北省衡水市武邑武罗学校2020-2021学年高二上学期期中数学试题云南省云南省昭通第一中学2019-2020学年高一下学期期中摸底考试数学试题甘肃省静宁县第一中学2020-2021学年高一下学期第三次月考数学(文)试题甘肃省静宁县第一中学2020-2021学年高一下学期第三次月考数学(文)(实验班)试题江西省抚州市南城一中2020-2021学年高一5月月考数学(文)试题江西省南城一中2020-2021学年高一4月月考数学(理)试题湖南省衡阳师范学院祁东附属中学2019-2020学年高二上学期期中数学试题广东省肇庆市高要区第二中学2020-2021学年高一下学期段考二数学试题云南省玉溪第二中学2020-2021学年高二下学期第一次月考数学(文)试题北京一零一中学2022届高三9月月考统练一数学试题(已下线)专题20 利用正(余)弦定理破解解三角形问题-备战2022年高考数学一轮复习一网打尽之重点难点突破山西省朔州市怀仁一中云东校区2019-2020学年高一下学期期中数学(文)试题河南省郑州市2021-2022学年高二上学期期中数学(理)试题河南省郑州市十校2021-2022学年高二上学期期中联考数学(理)试题广西桂林市中山中学2021-2022学年高二上学期期中质量检测数学(理)试题辽宁省六校协作体2021-2022学年高三上学期期中数学试题(已下线)专题06 盘点三角形面积与周长问题——备战2022年高考数学二轮复习常考点专题突破海南省琼海市嘉积第二中学2021-2022学年高一下学期教学质量监测(期末)数学试题黑龙江省哈尔滨市哈尔滨师范大学附属中学2021-2022学年高一下学期期末数学试题北京市北京中学2022-2023学年高二上学期期中考试数学试题河南省郑州外国语学校2022-2023学年高三上学期名校联考备考卷文科数学试题河南省安阳市安东新区第一高级中学2021-2022学年高二上学期9月考试数学试题河南省项城市第三高级中学2021-2022学年高二上学期10月第一次段考数学试题(A)(已下线)第08讲 正弦定理和余弦定理5种常见题型(2)江苏省扬州中学2022-2023学年高一下学期期中数学试题宁夏银川市贺兰县第二高级中学2023届高三第四次模考数学试题北京市中关村中学2024届高三上学期9月开学考试数学试题天津市新华中学2024届高三上学期第一次月考数学试题(已下线)模块一 专题5 平面向量与复数(1)(人教A)宁夏银川市育才中学2024届高三上学期第三次月考数学(理)试题黑龙江省伊春市铁力市马永顺中学校2024届高三上学期期中数学试题(已下线)专题04 平面向量的应用 (2)-【寒假自学课】(人教A版2019)(已下线)专题6.6 解三角形-举一反三系列(已下线)第6.4.3讲 正弦定理(第2课时)-同步精讲精练宝典(已下线)FHsx1225yl152天津市实验中学滨海学校2023-2024学年高一下学期随堂质量监测(月考)数学试题
9 . 已知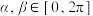 ,
,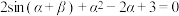 ,则
,则
______ .
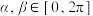 ,
,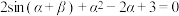 ,则
,则
您最近半年使用:0次
10 . 如图,八卦桥(图1)是洛南县地标性建筑之一,它是一个八边形人行天桥,桥的中心处建有一座五层高的宝塔(图2),晚上宝塔上的霓虹灯流光溢彩非常美丽.某同学为了测量宝塔的高度,在塔底部同一水平线上选取了C,D两点,测得塔的仰角分别为 和
和 ,C,D间的距离是12米.则宝塔的高度AB是( )米.(结果保留根号)
,C,D间的距离是12米.则宝塔的高度AB是( )米.(结果保留根号)
 和
和 ,C,D间的距离是12米.则宝塔的高度AB是( )米.(结果保留根号)
,C,D间的距离是12米.则宝塔的高度AB是( )米.(结果保留根号)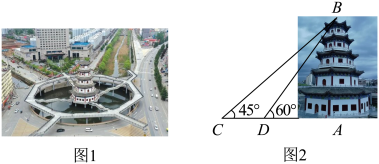
A. | B.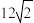 |
C.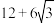 | D.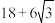 |
您最近半年使用:0次
2023-09-25更新
|
257次组卷
|
6卷引用:陕西省洛南中学2022-2023学年高一下学期期中数学试题
陕西省洛南中学2022-2023学年高一下学期期中数学试题陕西省西安市阎良区关山中学2024届高三上学期第一次质量检测数学(理)试题(已下线)专题13 余弦定理、正弦定理的应用-【寒假自学课】(苏教版2019)(已下线)11.3 余弦定理、正弦定理的应用-【帮课堂】(苏教版2019必修第二册)(已下线)第6.4.3讲 余弦定理、正弦定理的应用(第3课时)-同步精讲精练宝典(已下线)6.4.3.3 余弦定理、正弦定理应用举例——课后作业(基础版)



