1 . 已知数列 的前
的前 项和为
项和为 ,满足
,满足 ,当
,当 时,
时,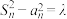 .给出下列四个结论:①当
.给出下列四个结论:①当 时,
时, ;
;
②当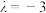 时,
时, ;
;
③当 时,
时,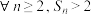 恒成立;
恒成立;
④当 时,
时, 从第三项起为递增数列.
从第三项起为递增数列.
其中所有正确结论的序号为_________ .
 的前
的前 项和为
项和为 ,满足
,满足 ,当
,当 时,
时,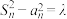 .给出下列四个结论:①当
.给出下列四个结论:①当 时,
时, ;
;②当
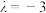 时,
时, ;
;③当
 时,
时,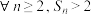 恒成立;
恒成立;④当
 时,
时, 从第三项起为递增数列.
从第三项起为递增数列.其中所有正确结论的序号为
您最近一年使用:0次
2 . 已知数列 满足:
满足: ,
,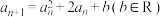 ,数列
,数列 的前
的前 项和为
项和为 ,则( )
,则( )
 满足:
满足: ,
,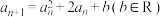 ,数列
,数列 的前
的前 项和为
项和为 ,则( )
,则( )A.当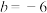 时,若 时,若 递增,则 递增,则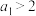 或 或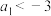 |
B.当 时,数列 时,数列 是递增数列 是递增数列 |
C.当 , , 时, 时,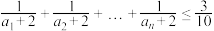 |
D.当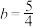 , , 时, 时, |
您最近一年使用:0次
2024高二下·上海·专题练习
解题方法
3 . 已知 为等差数列,
为等差数列, 为其前
为其前 项和,若
项和,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求 的最大值.
的最大值.
 为等差数列,
为等差数列, 为其前
为其前 项和,若
项和,若 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)求
 的最大值.
的最大值.
您最近一年使用:0次
4 . 已知函数 和数列
和数列 ,函数
,函数 在点
在点 处的切线的斜率记为
处的切线的斜率记为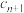 ,且已知
,且已知 .
.
(1)若数列 满足:
满足: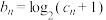 ,求数列
,求数列 的通项公式;
的通项公式;
(2)在(1)的条件下,若数列 满足
满足 ,
,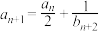 ,是否存在正整数n,使得
,是否存在正整数n,使得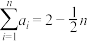 成立?若存在,求出所有n的值;若不存在,请说明理由.
成立?若存在,求出所有n的值;若不存在,请说明理由.
 和数列
和数列 ,函数
,函数 在点
在点 处的切线的斜率记为
处的切线的斜率记为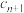 ,且已知
,且已知 .
.(1)若数列
 满足:
满足: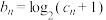 ,求数列
,求数列 的通项公式;
的通项公式;(2)在(1)的条件下,若数列
 满足
满足 ,
,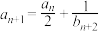 ,是否存在正整数n,使得
,是否存在正整数n,使得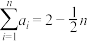 成立?若存在,求出所有n的值;若不存在,请说明理由.
成立?若存在,求出所有n的值;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
5 . 等差数列 中,
中, 为
为 的前n项和,
的前n项和,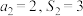 ,若不等式
,若不等式 ,对任意的
,对任意的 恒成立,则实数k的取值范围为
恒成立,则实数k的取值范围为_________ .
 中,
中, 为
为 的前n项和,
的前n项和,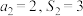 ,若不等式
,若不等式 ,对任意的
,对任意的 恒成立,则实数k的取值范围为
恒成立,则实数k的取值范围为
您最近一年使用:0次
2024-05-11更新
|
555次组卷
|
4卷引用:广东省华南师范大学附属中学2023-2024学年高二下学期期中考试数学试题
广东省华南师范大学附属中学2023-2024学年高二下学期期中考试数学试题广东省茂名市高州中学2023-2024学年高二下学期5月中旬模拟数学试题(已下线)专题1 数列的单调性与最值(范围)问题【讲】(高二期末压轴专项)山东省烟台市牟平区第一中学2023-2024学年高二下学期6月限时练(月考)数学试题
6 . 若存在等比数列 ,使得
,使得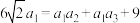 ,则公比
,则公比 的取值范围是
的取值范围是__________ .
 ,使得
,使得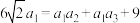 ,则公比
,则公比 的取值范围是
的取值范围是
您最近一年使用:0次
7 . 已知 是递增数列,则
是递增数列,则 的通项公式可能为( )
的通项公式可能为( )
 是递增数列,则
是递增数列,则 的通项公式可能为( )
的通项公式可能为( )A.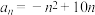 | B.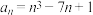 |
C. | D.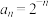 |
您最近一年使用:0次
2024-03-21更新
|
302次组卷
|
2卷引用:河北省邢台市五岳联盟2023-2024学年高二下学期3月月考数学试题
8 . 已知各项均不为0的数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求 的通项公式;
的通项公式;
(2)若对于任意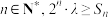 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,且
,且 .
.(1)求
 的通项公式;
的通项公式;(2)若对于任意
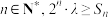 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-13更新
|
3809次组卷
|
10卷引用:湖北省七市州2024届高三下学期3月联合统一调研测试数学试题
湖北省七市州2024届高三下学期3月联合统一调研测试数学试题山东省潍坊市昌乐北大公学学校2024届高三下学期3月监测数学试题江苏省连云港市东海高级中学2023-2024学年高二下学期第一次月考数学试卷江西省丰城市第九中学2023-2024学年高二下学期4月月考数学试题重庆市乌江新高考协作体2023-2024学年高二下学期第一阶段学业质量联合调研抽测(4月)数学试题江西省南昌市第十九中学2023-2024学年高三下学期第一次模拟考试数学试卷(已下线)湖北省七市州2024届高三下学期3月联合统一调研测试数学试题变式题16-19辽宁省大连育明高级中学2023-2024学年高二下学期期中考试数学试卷(已下线)4.2.2等差数列的前n项和公式(3)甘肃省兰州市2024届高三下学期三模数学试题
2024高三下·全国·专题练习
解题方法
9 . 已知 和
和 都是等差数列,
都是等差数列, 的公差为
的公差为 ,且
,且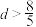 ,
,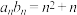 ,记
,记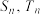 分别为数列
分别为数列 的前
的前 项和,且
项和,且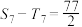 ,则
,则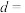
______ .
 和
和 都是等差数列,
都是等差数列, 的公差为
的公差为 ,且
,且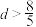 ,
,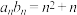 ,记
,记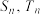 分别为数列
分别为数列 的前
的前 项和,且
项和,且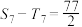 ,则
,则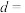
您最近一年使用:0次
名校
解题方法
10 . 已知数列 是首项为1,公差为2的等差数列,若
是首项为1,公差为2的等差数列,若 ,则
,则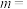
__________ .
 是首项为1,公差为2的等差数列,若
是首项为1,公差为2的等差数列,若 ,则
,则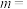
您最近一年使用:0次



