20-21高三下·浙江·阶段练习
名校
1 . 已知 ,函数
,函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)已知函数 存在极值点
存在极值点 、
、 ,求证:
,求证: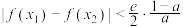 .
.
 ,函数
,函数 .
.(1)讨论函数
 的单调性;
的单调性;(2)已知函数
 存在极值点
存在极值点 、
、 ,求证:
,求证: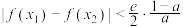 .
.
您最近一年使用:0次
2020·全国·模拟预测
2 . 已知函数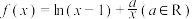 .
.
(1)求函数 的单调性;
的单调性;
(2)当 ,
, 时,
时,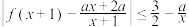 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
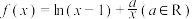 .
.(1)求函数
 的单调性;
的单调性;(2)当
 ,
, 时,
时,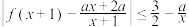 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
3 . 已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若 ,
, 且
且 ,都有
,都有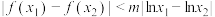 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 ,
, 且
且 ,都有
,都有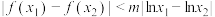 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-12-20更新
|
688次组卷
|
7卷引用:江苏省镇江市扬中市第二高级中学2023-2024学年高三上学期阶段检测一数学试题
江苏省镇江市扬中市第二高级中学2023-2024学年高三上学期阶段检测一数学试题(已下线)第五章 导数及其应用A卷(基础过关)-【双基双测】2021-2022学年高二数学同步单元AB卷(苏教版2019选择性必修第一册)江苏省镇江市扬中市第二高级中学2022-2023学年高二上学期期末考前热身数学试题重庆市南开中学2021届高三上学期第四次质量检测数学试题(已下线)人教A版选修2-2综合测试-2020-2021学年高二数学(理)下学期期末专项复习(人教A版)(已下线)河北省石家庄市精英中学2021届高三下学期阶段性数学试题(已下线)专题10 导数压轴解答题(综合类)-1
名校
4 . 已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)当 时,证明:
时,证明: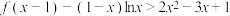 ;
;
(2)设实数 ,
,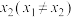 是函数
是函数 的两个零点,求实数
的两个零点,求实数 的取值范围.
的取值范围.
 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)当
 时,证明:
时,证明: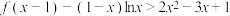 ;
;(2)设实数
 ,
,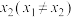 是函数
是函数 的两个零点,求实数
的两个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-11-23更新
|
886次组卷
|
2卷引用:八省市2021届高三新高考统一适应性考试江苏省无锡市天一中学考前热身模拟数学试题(二)
5 . 已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在定义域内有两个零点,求
在定义域内有两个零点,求 的取值范围;
的取值范围;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若函数
 在定义域内有两个零点,求
在定义域内有两个零点,求 的取值范围;
的取值范围;(3)若对任意
 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
6 . 已知函数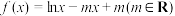 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若 在
在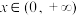 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),对任意的 ,证明:
,证明: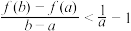 .
.
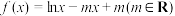 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 在
在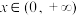 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(3)在(2)的条件下(提示:可以用第(2)问的结论),对任意的
 ,证明:
,证明: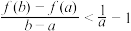 .
.
您最近一年使用:0次
2020-08-04更新
|
987次组卷
|
7卷引用:2020届江苏省徐州市新沂市第一中学高三下学期3月模拟考试数学试题
2020届江苏省徐州市新沂市第一中学高三下学期3月模拟考试数学试题河南省2020届高三5月份名校联盟高考数学(文科)模拟试题河南省名校联盟2020届高三5月质量检测数学文科试卷2020届河南省商丘周口市部分学校联考高三5月质量检测数学(文科)试题(已下线)专题03 导数及其应用——2020年高考真题和模拟题文科数学分项汇编(已下线)模块三 大招1 拉格朗日中值定理(已下线)专题10 利用微分中值法证明不等式【练】
7 . 已知函数 .
.
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)设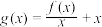 ,求函数
,求函数 的单调区间;
的单调区间;
(3)若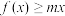 对任意的
对任意的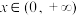 恒成立,求满足题意的所有整数m的取值集合.
恒成立,求满足题意的所有整数m的取值集合.
 .
.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)设
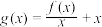 ,求函数
,求函数 的单调区间;
的单调区间;(3)若
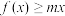 对任意的
对任意的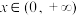 恒成立,求满足题意的所有整数m的取值集合.
恒成立,求满足题意的所有整数m的取值集合.
您最近一年使用:0次
2020-07-15更新
|
309次组卷
|
2卷引用:江苏省南通市2020届高三下学期第四次调研测试数学试题
名校
8 . 已知函数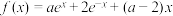 ,(
,( ,
, 是自然对数的底数).
是自然对数的底数).
(1)讨论 的单调性;
的单调性;
(2)当 时,
时,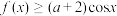 ,求
,求 的取值范围.
的取值范围.
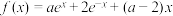 ,(
,( ,
, 是自然对数的底数).
是自然对数的底数).(1)讨论
 的单调性;
的单调性;(2)当
 时,
时,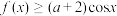 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-07-09更新
|
969次组卷
|
4卷引用:江苏省泰州中学2020届高三下学期第五次模拟考试数学试题
名校
9 . 设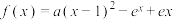 ,
,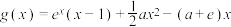 ,
, ,其中e为自然对数的底数(
,其中e为自然对数的底数(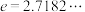 ).
).
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)设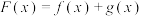 ,求
,求 的单调区间;
的单调区间;
(3)当 时,
时, 恒成立,求a的取值范围.
恒成立,求a的取值范围.
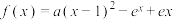 ,
,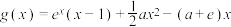 ,
, ,其中e为自然对数的底数(
,其中e为自然对数的底数(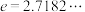 ).
).(1)当
 时,求
时,求 在
在 处的切线方程;
处的切线方程;(2)设
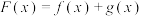 ,求
,求 的单调区间;
的单调区间;(3)当
 时,
时, 恒成立,求a的取值范围.
恒成立,求a的取值范围.
您最近一年使用:0次
2020-07-04更新
|
283次组卷
|
2卷引用:江苏省南京师大附中2020届高三下学期6月高考模拟数学试题
名校
10 . 已知函数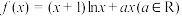 .
.
(1)若 在
在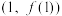 处的切线方程为
处的切线方程为 ,求实数
,求实数 ,
, 的值:
的值:
(2)求证:当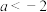 时,
时,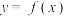 在
在 上有两个极值点:
上有两个极值点:
(3)设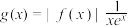 ,若
,若 在
在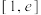 单调递减,求实数
单调递减,求实数 的取值范围.(其中
的取值范围.(其中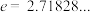 为自然对数的底数)
为自然对数的底数)
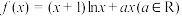 .
.(1)若
 在
在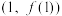 处的切线方程为
处的切线方程为 ,求实数
,求实数 ,
, 的值:
的值:(2)求证:当
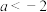 时,
时,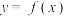 在
在 上有两个极值点:
上有两个极值点:(3)设
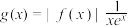 ,若
,若 在
在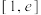 单调递减,求实数
单调递减,求实数 的取值范围.(其中
的取值范围.(其中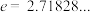 为自然对数的底数)
为自然对数的底数)
您最近一年使用:0次
2020-06-24更新
|
614次组卷
|
5卷引用:2020届江苏省新海高中、昆山中学、梁丰高中高三下学期5月高考模拟数学试题



