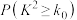解题方法
1 . 已知正实数 满足
满足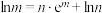 (
( 是自然对数的底数,
是自然对数的底数,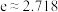 ),则( )
),则( )
 满足
满足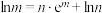 (
( 是自然对数的底数,
是自然对数的底数,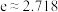 ),则( )
),则( )A. | B.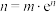 |
C.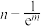 的最大值为 的最大值为 | D.方程 无实数解 无实数解 |
您最近一年使用:0次
2 . 杭州是国家历史文化名城,为了给来杭州的客人提供最好的旅游服务,某景点推出了预订优惠活动,下表是该景点在某App平台10天预订票销售情况:
经计算可得: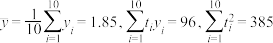 .
.
(1)因为该景点今年预订票购买火爆程度远超预期,该App平台在第10天时系统异常,现剔除第10天数据,求 关于
关于 的线性回归方程(结果中的数值用分数表示);
的线性回归方程(结果中的数值用分数表示);
(2)该景点推出团体票,每份团体票包含四张门票,其中 张为有奖门票(可凭票兑换景点纪念品),
张为有奖门票(可凭票兑换景点纪念品), 的分布列如下:
的分布列如下:
今从某份团体票中随机抽取2张,恰有1张为有奖门票,求该份团体票中共有3张有奖门票的概率.
附:对于一组数据 ,其回归线
,其回归线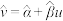 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: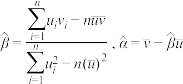
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售量 (万张) (万张) | 1.93 | 1.95 | 1.97 | 1.98 | 2.01 | 2.02 | 2.02 | 2.05 | 2.07 | 0.5 |
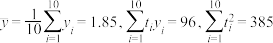 .
.(1)因为该景点今年预订票购买火爆程度远超预期,该App平台在第10天时系统异常,现剔除第10天数据,求
 关于
关于 的线性回归方程(结果中的数值用分数表示);
的线性回归方程(结果中的数值用分数表示);(2)该景点推出团体票,每份团体票包含四张门票,其中
 张为有奖门票(可凭票兑换景点纪念品),
张为有奖门票(可凭票兑换景点纪念品), 的分布列如下:
的分布列如下: | 2 | 3 | 4 |
 |  |  |  |
附:对于一组数据
 ,其回归线
,其回归线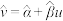 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: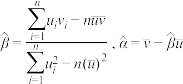
您最近一年使用:0次
2024-06-16更新
|
220次组卷
|
2卷引用:江苏省扬州市2024届高三下学期高考考前调研测试数学试题
名校
3 . 某外来入侵植物生长迅速,繁殖能力强,大量繁殖会排挤本地植物,容易形成单一优势种群,导致原有植物种群的衰退甚至消失,使当地生态系统的物种多样性下降,从而破坏生态平衡.假如不加控制,它的总数量每经过一年就增长一倍.则该外来入侵植物由入侵的1株变成100万株大约需要( )(参考数据: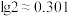 )
)
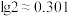 )
)| A.40年 | B.30年 | C.20年 | D.10年 |
您最近一年使用:0次
2024-06-16更新
|
131次组卷
|
2卷引用:江苏省扬州市2024届高三下学期高考考前调研测试数学试题
名校
解题方法
4 . 在四棱锥P−ABCD中,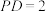 ,正方形ABCD的边长为2,
,正方形ABCD的边长为2, 平面ABCD,则下列选项正确的是( )
平面ABCD,则下列选项正确的是( )
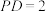 ,正方形ABCD的边长为2,
,正方形ABCD的边长为2, 平面ABCD,则下列选项正确的是( )
平面ABCD,则下列选项正确的是( )A.该四棱锥的外接球表面积为 |
B.若点E为PA的中点,则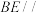 平面PDC 平面PDC |
C.若点Q在 内(含边界),且 内(含边界),且 ,则BQ长度的最大值为 ,则BQ长度的最大值为 |
D.若点M在正方形ABCD内(不含边界),且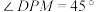 ,则四棱锥P−AMCD的体积的最大值为 ,则四棱锥P−AMCD的体积的最大值为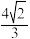 |
您最近一年使用:0次
名校
5 . 将正数 用科学记数法表示为
用科学记数法表示为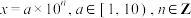 ,则把
,则把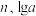 分别叫做
分别叫做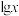 的首数和尾数,分别记为
的首数和尾数,分别记为 ,下列说法正确的是( )
,下列说法正确的是( )
 用科学记数法表示为
用科学记数法表示为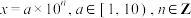 ,则把
,则把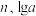 分别叫做
分别叫做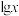 的首数和尾数,分别记为
的首数和尾数,分别记为 ,下列说法正确的是( )
,下列说法正确的是( )A.若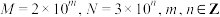 ,则 ,则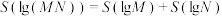 |
B.若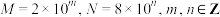 ,则 ,则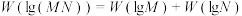 |
C.若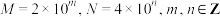 ,则 ,则 |
D.若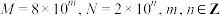 ,则 ,则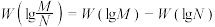 |
您最近一年使用:0次
2024-06-10更新
|
334次组卷
|
3卷引用:江苏省扬州中学2024届高三下学期全真模拟数学试卷
名校
6 . “直播的尽头是带货”,如今网络直播带货越来越火爆,但商品的质量才是一个主播能否持久带货的关键.某主播委托甲、乙两个工厂为其生产加工商品,为了了解商品质量情况,分别从甲、乙两个工厂各随机抽取了100件商品,根据商品质量可将其分为一、二、三等品,统计的结果如下图: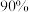 的把握认为商品为一等品与加工工厂有关?
的把握认为商品为一等品与加工工厂有关?
(2)将样本数据的频率视为概率,现在甲、乙工厂为该主播进行商品展示活动,每轮活动分别从甲、乙工厂中随机挑选一件商品进行展示,求在两轮活动中恰有三个一等品的概率;
(3)综合各个方面的因素,最终该主播决定以后只委托甲工厂为其生产商品,已知商品随机装箱出售,每箱30个.商品出厂前,工厂可自愿选择是否对每箱商品进行检验.若执行检验,则每个商品的检验费用为10元,并将检验出的三等品更换为一等品或二等品;若不执行检验,则对卖出的每个三等品商品支付100元赔偿费用.将样本数据的频率视为概率,以整箱检验费用的期望记为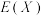 ,所有赔偿费用的期望记为
,所有赔偿费用的期望记为 ,以
,以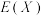 和
和 的大小关系作为决策依据,判断是否需要对每箱商品进行检验?请说明理由.
的大小关系作为决策依据,判断是否需要对每箱商品进行检验?请说明理由.


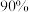 的把握认为商品为一等品与加工工厂有关?
的把握认为商品为一等品与加工工厂有关?(2)将样本数据的频率视为概率,现在甲、乙工厂为该主播进行商品展示活动,每轮活动分别从甲、乙工厂中随机挑选一件商品进行展示,求在两轮活动中恰有三个一等品的概率;
(3)综合各个方面的因素,最终该主播决定以后只委托甲工厂为其生产商品,已知商品随机装箱出售,每箱30个.商品出厂前,工厂可自愿选择是否对每箱商品进行检验.若执行检验,则每个商品的检验费用为10元,并将检验出的三等品更换为一等品或二等品;若不执行检验,则对卖出的每个三等品商品支付100元赔偿费用.将样本数据的频率视为概率,以整箱检验费用的期望记为
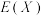 ,所有赔偿费用的期望记为
,所有赔偿费用的期望记为 ,以
,以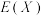 和
和 的大小关系作为决策依据,判断是否需要对每箱商品进行检验?请说明理由.
的大小关系作为决策依据,判断是否需要对每箱商品进行检验?请说明理由.
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次
2024-06-02更新
|
771次组卷
|
2卷引用:江苏省扬州市第一中学2023-2024学年高二下学期5月教学质量调研评估数学试题
名校
7 . 已知P是边长为1的正六边形 内一点(含边界),且
内一点(含边界),且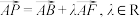 ,则下列正确的是( )
,则下列正确的是( )
 内一点(含边界),且
内一点(含边界),且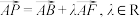 ,则下列正确的是( )
,则下列正确的是( )A.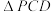 的面积为定值 的面积为定值 | B. 使得 使得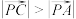 |
C. 的取值范围是 的取值范围是 | D.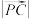 的取值范围是 的取值范围是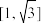 |
您最近一年使用:0次
2024-05-08更新
|
259次组卷
|
3卷引用:江苏省扬州市新华中学2023-2024学年高一下学期5月月考数学试题
江苏省扬州市新华中学2023-2024学年高一下学期5月月考数学试题广东省广州市增城中学2023-2024学年高一下学期期中数学试题(已下线)专题3 以平面几何图形为背景的向量综合问题【练】(高一期末压轴专项)
名校
8 . 已知焦点在 轴上,中心在坐标原点的等轴双曲线
轴上,中心在坐标原点的等轴双曲线 经过点
经过点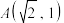 ,过点
,过点 作两条互相垂直的直线分别交双曲线于
作两条互相垂直的直线分别交双曲线于 两点.
两点.
(1)若 为等腰直角三角形,求边
为等腰直角三角形,求边 所在的直线方程;
所在的直线方程;
(2)判断原点 与
与 的外接圆的位置关系,并说明理由.
的外接圆的位置关系,并说明理由.
 轴上,中心在坐标原点的等轴双曲线
轴上,中心在坐标原点的等轴双曲线 经过点
经过点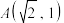 ,过点
,过点 作两条互相垂直的直线分别交双曲线于
作两条互相垂直的直线分别交双曲线于 两点.
两点.(1)若
 为等腰直角三角形,求边
为等腰直角三角形,求边 所在的直线方程;
所在的直线方程;(2)判断原点
 与
与 的外接圆的位置关系,并说明理由.
的外接圆的位置关系,并说明理由.
您最近一年使用:0次
9 . 一个三棱锥形木料 ,其中
,其中 是边长为
是边长为 的等边三角形,
的等边三角形, 底面
底面 ,二面角
,二面角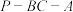 的大小为
的大小为 ,则点A到平面PBC的距离为
,则点A到平面PBC的距离为__________  .若将木料削成以A为顶点的圆锥,且圆锥的底面在侧面PBC内,则圆锥体积的最大值为
.若将木料削成以A为顶点的圆锥,且圆锥的底面在侧面PBC内,则圆锥体积的最大值为_________  .
.
 ,其中
,其中 是边长为
是边长为 的等边三角形,
的等边三角形, 底面
底面 ,二面角
,二面角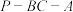 的大小为
的大小为 ,则点A到平面PBC的距离为
,则点A到平面PBC的距离为 .若将木料削成以A为顶点的圆锥,且圆锥的底面在侧面PBC内,则圆锥体积的最大值为
.若将木料削成以A为顶点的圆锥,且圆锥的底面在侧面PBC内,则圆锥体积的最大值为 .
.
您最近一年使用:0次
2024-03-27更新
|
869次组卷
|
5卷引用:江苏省扬州市高邮市临泽中学2024届高三下学期一模模拟数学试题
江苏省扬州市高邮市临泽中学2024届高三下学期一模模拟数学试题江苏省南通市海安高级中学2024届高三下学期开学考试数学试题江苏省南通市海安市2023-2024学年高三上学期期初学业质量监测数学试题河南省南阳市西峡县第一高级中学2023-2024学年高二下学期第一次调研测试数学试卷(已下线)第四章 立体几何解题通法 专题五 平移变换法 微点3 平移变换法综合训练【培优版】
名校
10 . 如果存在实数对 使函数
使函数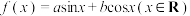 ,那么我们就称函数
,那么我们就称函数 为实数对
为实数对 的“正余弦生成函数”,实数对
的“正余弦生成函数”,实数对 为函数
为函数 的“生成数对”;
的“生成数对”;
(1)求函数 的“生成数对”;
的“生成数对”;
(2)若实数对 的“正余弦生成函数”
的“正余弦生成函数” 在
在 处取最大值,其中
处取最大值,其中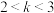 ,求
,求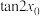 的取值范围;
的取值范围;
(3)已知实数对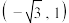 为函数
为函数 的“生成数对”,试问:是否存在正实数
的“生成数对”,试问:是否存在正实数 使得函数
使得函数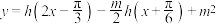 的最大值为
的最大值为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 使函数
使函数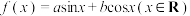 ,那么我们就称函数
,那么我们就称函数 为实数对
为实数对 的“正余弦生成函数”,实数对
的“正余弦生成函数”,实数对 为函数
为函数 的“生成数对”;
的“生成数对”;(1)求函数
 的“生成数对”;
的“生成数对”;(2)若实数对
 的“正余弦生成函数”
的“正余弦生成函数” 在
在 处取最大值,其中
处取最大值,其中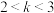 ,求
,求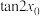 的取值范围;
的取值范围;(3)已知实数对
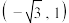 为函数
为函数 的“生成数对”,试问:是否存在正实数
的“生成数对”,试问:是否存在正实数 使得函数
使得函数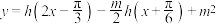 的最大值为
的最大值为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
2024-03-25更新
|
486次组卷
|
3卷引用:江苏省高邮市2023-2024学年高三下学期3月学情调研测试数学试题