真题
1 . 已知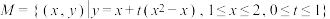 是平面直角坐标系中的点集.设
是平面直角坐标系中的点集.设 是
是 中两点间距离的最大值,
中两点间距离的最大值, 是
是 表示的图形的面积,则( )
表示的图形的面积,则( )
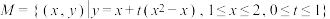 是平面直角坐标系中的点集.设
是平面直角坐标系中的点集.设 是
是 中两点间距离的最大值,
中两点间距离的最大值, 是
是 表示的图形的面积,则( )
表示的图形的面积,则( )A. , , | B. , , |
C.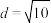 , , | D.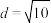 , , |
您最近一年使用:0次
7日内更新
|
2567次组卷
|
8卷引用:2024年北京高考数学真题
2024年北京高考数学真题(已下线)2024年北京高考数学真题变式题6-10专题03函数概念与基本初等函数(已下线)五年北京专题02函数概念与基本初等函数(已下线)三年北京专题02函数概念与基本初等函数(已下线)五年北京专题01集合、常用逻辑与不等式专题02函数(已下线)平面解析几何-综合测试卷B卷
2 . 汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直径依次为 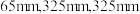 ,且斛量器的高为
,且斛量器的高为 ,则斗量器的高为
,则斗量器的高为______  ,升量器的高为
,升量器的高为________  .
.
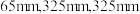 ,且斛量器的高为
,且斛量器的高为 ,则斗量器的高为
,则斗量器的高为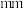 ,升量器的高为
,升量器的高为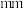 .
.
您最近一年使用:0次
2024-06-15更新
|
2578次组卷
|
6卷引用:2024年北京高考数学真题
2024年北京高考数学真题(已下线)2024年北京高考数学真题变式题11-15(已下线)五年北京专题06立体几何与空间向量(已下线)三年北京专题06立体几何与空间向量专题07立体几何与空间向量专题08立体几何与空间向量(第一部分)
真题
名校
3 . 某地区上年度电价为0.8元/kW•h,年用电量为akW•h,本年度计划将电价降到0.55元/kW•h至0.75元/kW•h之间,而用户期望电价为0.4元/kW•h,经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k).该地区电力的成本为0.3元/kW•h.
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(2)设 ,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
(注:收益=实际用电量×(实际电价﹣成本价))
(1)写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(2)设
 ,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?
,当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%?(注:收益=实际用电量×(实际电价﹣成本价))
您最近一年使用:0次
2024-01-03更新
|
198次组卷
|
48卷引用:2000年普通高等学校招生考试数学(文)试题(京、皖卷)
2000年普通高等学校招生考试数学(文)试题(京、皖卷)2000年普通高等学校招生考试数学(理)试题(京、皖卷)(已下线)大连市第23中2009-2010学年度高二下学期期中考试(文科)(已下线)2010年辽宁省庄河市第六高级中学高一上学期第一次月考数学卷江苏省镇江市镇江中学2019-2020学年高一上学期第一次月考数学试题上海市静安区新中高级中学2017-2018学年高一上学期10月月考数学试题人教A版(2019) 必修第一册 逆袭之路 第三章 函数的概念与性质 小结上海市复旦中学2017-2018学年高一上学期10月月考数学试题重庆市南开中学2021届高三上学期8月月考数学试题(已下线)重庆市第八中学2021届高上学期三8月月考数学试题(已下线)2.3+第2课时+一元二次不等式的应用(分层练习)-2020-2021学年高一数学新教材配套练习(人教A版必修第一册)湖南省常德市第二中学2020-2021学年高一上学期第一次测试数学试题(已下线)【新东方】在线数学 (2)天津市河西区2020-2021学年高一上学期期中数学试题山东省青岛胶州市2020-2021学年高一上学期期中考试数学试题山东省青岛市黄岛区2020-2021学年高一上学期期中考试数学试题江苏省南通市2021届高三下学期3月模拟数学试题人教A版(2019) 必修第一册 新高考名师导学 第三章 复习参考题3福建省三明市第一中学2020-2021学年高一下学期开学考试数学试题江苏省镇江一中2019-2020学年高一上学期10月第一次月考数学试题(已下线)考点突破03 函数的概念与性质-备战2022年高考数学一轮复习培优提升精炼(新高考地区专用)(已下线)2.3 第2课时 一元二次不等式的应用(分层练习)-2021-2022学年高一数学教材配套学案+练习(人教A版2019必修第一册)(已下线)2.3 (分层练)二次函数与一元二次方程、不等式-2021-2022学年高中数学必修第一册课时解读与训练(人教A版2019)(已下线)3.4 函数的应用(一)- 2021-2022高一上学期数学新教材配套提升训练(人教A版2019必修第一册)(已下线)上海市华东师范大学第二附属中学2021-2022学年高一上学期10月月考数学试题(已下线)复习参考题3苏教版(2019) 必修第一册 过关检测 第3章 第3.3节综合把关(已下线)2.3.2 一元二次不等式的应用-2021-2022学年高一数学考点讲解练(人教A版2019必修第一册)(已下线)专题3.4 函数的应用(一)-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册) 甘肃省张掖市某重点校2022-2023学年高三上学期第二次检测数学(文)试题新疆克孜勒苏柯尔克孜自治州第一中学2023届高三上学期11月期中考试数学(文)试题山东省青岛第一中学、青岛第九中学2020-2021学年高一上学期期中考试数学试题广东省惠州市华罗庚中学2022-2023学年高一上学期11月月考数学试题广东省江门市第二中学2022-2023学年高一上学期期中数学试题1.4.3 一元二次不等式的应用 同步练习-2022-2023学年北师大版(2019)必修第一册人教A版(2019)必修第一册课本习题第三章复习参考题(已下线)考点14 常见函数应用模型 2024届高考数学考点总动员【练】江苏省南京师范大学灌云附属中学2023-2024学年高一上学期期初摸底考试数学试题上海市建平中学2023-2024学年高一上学期10月月考数学试题湖南省岳阳市湘阴县知源高级中学2023-2024学年高一上学期第一次月考数学试题湖北省荆州市石首市第一中学2022-2023学年高一上学期9月月考数学试题(已下线)期中真题必刷压轴60题(15个考点专练)-【满分全攻略】(人教A版2019必修第一册)湖南省长沙市长郡中学2022-2023学年高一上学期期中复习数学试题山东省临沂市莒南县2023-2024学年高一上学期期中学业质量检测数学试题陕西省西安市碑林区教育局2023-2024学年高一上学期教育质量监测数学试题(已下线)第四章 指数函数与对数函数(压轴必刷30题6种题型专项训练)-【满分全攻略】(人教A版2019必修第一册)云南省昆明市官渡区第五中学2023-2024学年高一上学期期中测试数学试卷(已下线)专题04 一元二次不等式
真题
名校
4 . 双曲线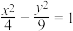 的渐近线方程是( )
的渐近线方程是( )
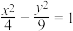 的渐近线方程是( )
的渐近线方程是( )A.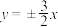 | B.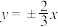 | C.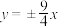 | D.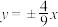 |
您最近一年使用:0次
2023-11-21更新
|
2693次组卷
|
68卷引用:2004 年普通高等学校春季招生考试数学(理)试题(北京卷)
2004 年普通高等学校春季招生考试数学(理)试题(北京卷)2004 年普通高等学校春季招生考试数学(文)试题(北京卷)【区级联考】北京市丰台区2018-2019学年高二上学期期末考试数学试题(已下线)2011年湖南省长沙市铁路一中高二上学期期末检测数学理卷(已下线)2011年湖南省长沙市铁路一中高二上学期期末检测数学文卷(已下线)2011年福建省福州市第八中学高二上学期期末考试数学文卷(已下线)2011年河南省许昌市部分学校高二上学期期末联考数学理卷(已下线)2010-2011年山西省孝义市三中高二第二次月考考试数学理卷(已下线)2011年新人教版高二上学期单元考试数学(已下线)2011—2012学年度甘肃省张掖二中高二月考理科数学试卷(已下线)2011-2012学年湖南省蓝山二中高二上学期期末考试文科数学试卷(已下线)2012年苏教版高中数学选修2-1 2.3双曲线练习卷(已下线)2013-2014学年福建省漳州一中高二上学期期末考理科数学试卷2014-2015学年甘肃省秦安县二中高二上学期第四次月考理科数学试卷2016-2017学年广东清远清城区三中高二文上学期第二次月考数学试卷浙江省余姚中学2017-2018学年高二上学期第一次质量检测试题数学四川省雅安市2017-2018学年高二上学期期末考试数学(理)试题四川省雅安市2017-2018学年高二上学期期末考试数学(文)试题广西贺州市2017-2018学年高二年级上学期期末质量检测数学(文)试题广西贺州市2017-2018学年高二上学期期末质量检测数学(理)试题【全国百强校】广东省中山市第一中学2017-2018学年高二下学期第二次段考数学(文)试题【全国百强校】宁夏石嘴山市第三中学2017-2018学年高二上学期第二次(12月)月考数学(文)试题【全国百强校】黑龙江省牡丹江市第一高级中学2018-2019学年高二上学期期中考试数学(文)试题【全国百强校】内蒙古杭锦后旗奋斗中学2018-2019学年高二上学期第二次(12月)月考数学(文)试题【校级联考】黑龙江省牡丹江市第三高级中学2018-2019学年高二上学期期中考试数学试题新疆实验中学2018-2019学年高二上学期期末考试数学(文)试题黑龙江省齐齐哈尔市龙江二中2019-2020学年高二上学期12月月考数学(文)试卷吉林省吉林市丰满区第五十五中学2019-2020学年高二上学期期末数学(文)试题四川省南充市2018-2019学年高二下学期期末数学(文)试题四川省南充市2018-2019学年高二下学期期末数学(理)试题(已下线)秒杀题型05 双曲线的渐近线(双曲线)-2020年高考数学试题调研之秒杀圆锥曲线压轴题黑龙江省伊春林业管理局第二中学2019-2020学年高二质量检测数学(理)试题江苏省南京市五校2020-2021学年高二上学期10月联合调研考试数学试题江苏省南京市扬子二中2020-2021学年高二10月月考数学试题广西桂林市第十八中学2020-2021学年高二上学期期中考试数学(文)试题广西桂林市第十八中学2020-2021学年高二上学期期中考试数学(理)试题四川省广安市代市中学校2021-2022学年高二上学期第二次月考数学(文)试题四川省资阳市2021-2022学年高二下学期期末质量检测数学(理)试题四川省资阳市2021-2022学年高二下学期期末数学文科试题山西省晋中市平遥县第二中学校2022-2023学年高二上学期10月质检数学试题新疆生产建设兵团第二师八一中学2023届高三上学期开学考试数学(文)试题陕西省西安市2022-2023学年高二上学期第二次考试理科数学试题江苏省南通市海安高级中学2022-2023学年高二上学期开学数学试题广东省茂名市电白区2022-2023学年高二上学期期末数学试题江苏省常州市第三中学2022-2023学年高二上学期期末数学试题广东省广州市第六十五中学2022-2023学年高二上学期期末数学试题四川省宜宾市叙州区第二中学校2022-2023学年高二下学期4月月考理科数学试题四川省成都市简阳市阳安中学2022-2023学年高二下学期期中考试数学(理)试题新疆巴音郭楞蒙古自治州第一中学2022-2023学年高二下学期开学摸底数学试题北师大版(2019) 选修第一册 数学奇书 学业评价(十六) 双曲线的简单几何性质四川省宜宾市叙州区第二中学校2022-2023学年高二下学期4月月考文科数学试题广西桂林市桂林中学2020-2021学年高二下学期期中数学(文)试题四川省雅安市天立学校2022-2023学年高二上学期期中考试数学(文科)试题四川省雅安市天立学校2022-2023学年高二上学期期中考试数学(理科B)试题四川省雅安市天立学校2022-2023学年高二上学期期中考试数学(理科A)试题 福建省福州市台江区福州四中2023-2024学年高二上学期期中数学试题福建省厦门市国贸协和双语高级中学有限公司2023-2024学年高二上学期11月期中考试数学试题福建省厦门市国贸协和双语高级中学2023-2024学年高二上学期第二次月考数学试题新疆乌鲁木齐第六十一中学2023-2024学年高二上学期11月期中考试数学试题河北省保定市定州中学2023-2024学年高二上学期12月月考数学试题天津市和平区耀华中学2023-2024学年高二上学期12月月考数学试题广东省广州市广州四中2023-2024学年高二上学期12月月考数学试题江苏省镇江市镇江中学2023-2024学年高二上学期期中数学试题陕西省汉中市西乡县第一中学2023-2024学年高二上学期第二次(12月)月考数学试题浙江省杭州市富阳区实验中学2023-2024学年高二上学期12月月考数学试题(已下线)第三章:圆锥曲线的方程章末综合检测卷-【题型分类归纳】2023-2024学年高二数学同步讲与练(人教A版2019选择性必修第一册)浙江省杭州市第四中学下沙校区2023-2024学年高二上学期期中数学试题云南省昆明市2024届”三诊一模“高三复习教学质量检测数学试题
5 . 经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度υ(千米/小时)之间的函数关系为: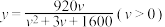 .
.
(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
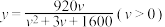 .
.(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
您最近一年使用:0次
2023-09-14更新
|
1384次组卷
|
56卷引用:2005年普通高等学校春季招生考试数学(理)试题(北京卷)
2005年普通高等学校春季招生考试数学(理)试题(北京卷)2005年普通高等学校春季招生考试数学(文)试题(北京卷)北京市清华大学附属中学朝阳学校2023-2024学年高一上学期10月月考数学试题(已下线)2012年人教B版高中数学必修5 3.4 不等式的实际应用练习卷广东省佛山市华南师范大学附中南海实验高级中学2018-2019学年高一下学期6月月考数学试题山东省枣庄市第八中学2019-2020学年高一上学期期中数学试题山东省枣庄市2019-2020学年高一上学期11月月考数学试题上海市青浦区2016-2017学年高一上学期期终学业质量调研测试数学试题河南省濮阳市2019-2020学年高二上学期期末数学(理)试题河南省濮阳市2019-2020学年高二上学期期末数学(文)试题山东省济宁市兖州区2019-2020学年高一上学期期中数学试题新疆生产建设兵团五校2017-2018学年高一下学期期末联考数学(文)试题江苏省连云港市锦屏高级中学2018-2019学年高二上学期期中数学试题山东省烟台市招远市第一中学2019-2020学年高二上学期期中数学试题山东省济宁市第二中学2019-2020学年高一上学期10月月考数学试题山东省枣庄市滕州二中2019-2020学年高一(10月份)第一次质量检测数学试题山东省济宁市鱼台县第一中学2020-2021学年高一上学期第一次月考(10月)数学试题辽宁省大连八中2019-2020学年高一10月月考数学试题河北省保定市徐水区第一中学2020-2021学年高一上学期10月月考数学试题第二章+等式与不等式(基础过关)-2020-2021学年高一数学单元测试定心卷(人教B版2019必修第一册)江苏省苏州市星海中学2020-2021学年高二上学期期中数学试题江苏省连云港市市区三星普通高中2020-2021学年高二上学期期中联考数学试题(已下线)2.2 基本不等式(精炼)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教版A版)江西省九江市六校2020-2021学年高一下学期期末数学试题(已下线)专题2.2 基本不等式专题突破 B卷-2021-2022学年高一数学单元卷模拟(易中难)(2019人教A版必修第一册)(已下线)期末复习【真题训练】-2020-2021学年高一数学单元复习(沪教版2020必修第一册)(已下线)专题1.8 基本不等式-重难点题型精练-2022年高考数学一轮复习举一反三系列(新高考地区专用)山东省菏泽市郓城第一中学2021-2022学年高三上学期第一次阶段性检测数学试题江苏省宿迁市沭阳县修远中学2021-2022学年高一上学期第一次月考数学试题山东省聊城第一中学2021-2022学年高三上学期期中数学试题新疆莎车县第一中学2021-2022学年高一上学期第三次质量检测数学试题甘肃省兰州市第一中学2021-2022学年高一上学期期中考试数学试题河南省驻马店市环际大联考2021-2022学年高二上学期期中考试理科数学试题河南省驻马店市环际大联考2021-2022学年高二上学期期中考试文科数学试题浙江省温州市苍南县金乡卫城中学2022-2023学年高一上学期第一次月考数学试题山东省德州市三校2022-2023学年高一上学期9月校际联考数学试题辽宁省沈阳市第二十中学2022-2023学年高一上学期期初考试数学试题湖南省衡阳市田家炳实验中学2022-2023学年高一上学期期中数学试题(已下线)第07讲 基本不等式及其应用(2大考点4种解题方法)(1)湖北省武汉市江汉区2022-2023学年高一上学期期中模拟数学试题湖北省十堰市天河英才高中2022-2023学年高一上学期10月月考数学试题陕西省宝鸡市陈仓区2022-2023学年高一上学期期中数学试题湖南省长沙市长郡梅溪湖中学2022-2023学年高二下学期期中数学试题湖北省武汉市江汉区2022-2023学年高一上学期期中数学试题人教A版(2019) 必修第一册 数学奇书 第二章 一元二次函数、方程和不等式 2.2 基本不等式 第2课时 基本不等式的综合应用北师大版(2019) 必修第一册 数学奇书 第一章 预备知识 §3 不等式 §3.2 基本不等式 第2课时 基本不等式的应用(已下线)高一上学期期中【压轴60题考点专练】(必修一前三章)-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)(已下线)高一数学上学期期末【全真模拟卷02】-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)(已下线)第3章 不等式综合能力测试-【帮课堂】(苏教版2019必修第一册)(已下线)第二章 一元二次函数、方程和不等式(章末测试A卷)-同步精品课堂(人教A版2019必修第一册)吉林省长春博硕学校2023-2024学年高一上学期第一次阶段性测试数学试题黑龙江省哈尔滨市第三中学2023-2024学年高一上学期第一次验收考试数学试题江苏省无锡市辅仁高级中学2023-2024学年高一上学期教学质量抽测(一)数学试题河南省郑州市十所省级示范性高中2023-2024学年高一上学期期中联考数学试题陕西省咸阳市实验中学2022-2023学年高一上学期第一次月考数学试题广东省鹤山市第一中学2023-2024高一上学期第一阶段考试数学试题
6 . 若直线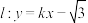 与直线
与直线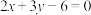 的交点位于第一象限,则直线
的交点位于第一象限,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
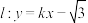 与直线
与直线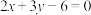 的交点位于第一象限,则直线
的交点位于第一象限,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )A. | B.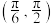 |
C. | D.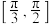 |
您最近一年使用:0次
2023-08-08更新
|
1751次组卷
|
29卷引用:2002年普通高等学校招生考试数学(文)试题(北京卷)
2002年普通高等学校招生考试数学(文)试题(北京卷)(已下线)2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷2015-2016学年河南省鹤壁市高一上学期期末数学试卷2015-2016学年湖北省黄冈中学高二上第四次周测数学试卷2017届河北武邑中学高三理周考12.4数学试卷河北省定州中学2016-2017学年高一(承智班)下学期期末考试数学试题陕西省黄陵中学2016-2017学年高一(普通班)下学期第四学月考试数学试题山西省大同市第一中学2017-2018学年高二上学期期中考试数学试题1山西省大同市第一中学2017-2018学年高二上学期期中考试数学试题2河北省阜城中学2017-2018学年高一上学期第六次月考数学(文)试题陕西省宝鸡市金台区2020-2021学年高一上学期期末数学试题(已下线)1.4 两条直线的交点(A 基础培优练)-2021-2022学年高二数学上学期同步双培优检测(苏教版2019选择性必修第一册)(已下线)第二章 直线和圆的方程单元测试与方法突破-2021-2022学年高二数学10分钟课前预习练(人教A版2019选择性必修第一册)(已下线)第10讲 两条直线的交点坐标-【帮课堂】(已下线)2.2.3 两条直线的位置关系(已下线)专题02 史上最全直线的最值问题(2)江苏省徐州市王杰中学2021-2022学年高二10月阶段性测试数学试题沪教版(2020) 一轮复习 堂堂清 第七单元 7.10 直线与圆锥曲线的应用(一)沪教版(2020) 一轮复习 堂堂清 第七单元 7.1 直线的倾斜角与斜率河南省信阳高级中学2022-2023学年高二上学期10月月考数学试题北京名校2023届高三一轮总复习 第7章 解析几何 7.1 直线的斜率与直线方程陕西省渭南市白水县2020~2021学年高一上学期期末数学试题(已下线)第15讲 直线的交点坐标与距离公式6种常见考法归类(3)(已下线)第一节 直线的方程 A素养养成卷(已下线)考点01 直线的倾斜角与斜率 2024届高考数学考点总动员河南省南阳市南召现代中学2023-2024学年高二上学期第一次月考数学试题广东省深圳外国语学校(集团)龙华高中部2023-2024学年高二上学期期中数学试题(已下线)2.1.1 倾斜角与斜率【第三课】
7 . 在 中,内角
中,内角 满足
满足 ,则
,则 的形状为
的形状为 ( )
( )
| A.直角三角形 | B.等腰三角形 |
| C.等腰直角三角形 | D.正三角形 |
您最近一年使用:0次
2023-06-25更新
|
2298次组卷
|
22卷引用:2005年普通高等学校春季招生考试数学(理)试题(北京卷)
2005年普通高等学校春季招生考试数学(理)试题(北京卷)2005年普通高等学校春季招生考试数学(文)试题(北京卷)北京市石景山区2022-2023学年高一下学期期末考试数学试题(已下线)专题04 正余弦定理4种常考题型归类-《期末真题分类汇编》(北京专用)【北京专用】专题08解三角形(第一部分)-高一下学期名校期末好题汇编广西贺州市平桂高级中学2020-2021学年高二上学期第一次月考数学试题湖南省怀化市2020-2021学年高二上学期期末数学试题上海市华东师范大学附属枫泾中学2020-2021学年高一下学期第一次月考数学试题(已下线)第11课时 课后 二倍角的正弦、余弦、正切公式宁夏青铜峡市高级中学2022届高三上学期期中考试数学(文)试题安徽省合肥市第一中学2021-2022学年高三上学期11月月考文科数学试题辽宁省营口市第二高级中学2021-2022学年高一下学期第一次月考数学试题四川省内江市威远中学校2021-2022学年高一下学期第一次月考数学(理)试题四川省内江市威远中学校2021-2022学年高一下学期第一次月考数学(文)试题重庆市江津实验中学校2022-2023学年高一下学期期中数学试题河北省承德市双滦区实验中学2022-2023学年高一下学期5月月考数学试题天津市西青区当城中学2022-2023学年高一下学期期中数学试题(已下线)模块三 专题5 三角恒等变换(基础卷A)河南省南阳市邓州春雨国文学校2023-2024学年高二上学期8月月考数学试题(已下线)【第三课】5.5.1课时1 两角和与差的正弦、余弦公式河北省石家庄二中2023-2024学年高一下学期期中数学试题(已下线)专题03 恒等变形拆角归类(2) -期末考点大串讲(苏教版(2019))
8 . 已知椭圆 的离心率为
的离心率为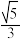 ,A、C分别是E的上、下顶点,B,D分别是
,A、C分别是E的上、下顶点,B,D分别是 的左、右顶点,
的左、右顶点,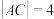 .
.
(1)求 的方程;
的方程;
(2)设 为第一象限内E上的动点,直线
为第一象限内E上的动点,直线 与直线
与直线 交于点
交于点 ,直线
,直线 与直线
与直线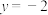 交于点
交于点 .求证:
.求证: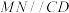 .
.
 的离心率为
的离心率为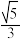 ,A、C分别是E的上、下顶点,B,D分别是
,A、C分别是E的上、下顶点,B,D分别是 的左、右顶点,
的左、右顶点,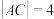 .
.(1)求
 的方程;
的方程;(2)设
 为第一象限内E上的动点,直线
为第一象限内E上的动点,直线 与直线
与直线 交于点
交于点 ,直线
,直线 与直线
与直线 交于点
交于点 .求证:
.求证: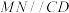 .
.
您最近一年使用:0次
2023-06-19更新
|
16203次组卷
|
24卷引用:2023年北京高考数学真题
2023年北京高考数学真题(已下线)北京十年真题专题08平面解析几何北京十年真题专题08平面解析几何(已下线)高考数学测试 请勿下载专题12平面解析几何(第二部分)(已下线)五年北京专题08平面解析几何(已下线)三年北京专题08平面解析几何专题07平面解析几何(成品)(已下线)2023年北京高考数学真题变式题16-21第三章 圆锥曲线的方程 (单元测)(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(3)(已下线)第05讲 椭圆及其性质(练习)(已下线)考点14 直线与圆锥曲线相交问题 2024届高考数学考点总动员【练】(已下线)第08讲 直线与圆锥曲线的位置关系(练习)湖北省荆州市松滋市第一中学2024届高三上学期12月月考模拟数学试题(二)黑龙江省哈尔滨市第九中学校2023-2024学年高三下学期开学考试数学试题河北省保定市高碑店市崇德实验中学2024届高三上学期期末数学试题(已下线)思想04 运用转化与化归的思想方法解题(4大核心考点)(讲义)(已下线)专题8.2 椭圆综合【九大题型】(已下线)重难点14 圆锥曲线必考压轴解答题全归类【十一大题型】(举一反三)(新高考专用)-2(已下线)信息必刷卷05(天津专用)(已下线)专题24 解析几何解答题(理科)-1(已下线)专题24 解析几何解答题(文科)-3专题08平面解析几何
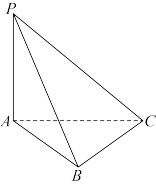
9 . 如图,在三棱锥 中,
中, 平面
平面 ,
,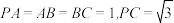 .
. 平面PAB;
平面PAB;
(2)求二面角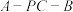 的大小.
的大小.
 中,
中, 平面
平面 ,
,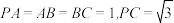 .
.
 平面PAB;
平面PAB;(2)求二面角
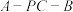 的大小.
的大小.
您最近一年使用:0次
2023-06-19更新
|
21853次组卷
|
32卷引用:2023年北京高考数学真题
2023年北京高考数学真题北京十年真题专题07立体几何与空间向量北京市昌平区首都师范大学附属回龙观育新学校2023-2024学年高二上学期10月月考数学试题(已下线)高考数学测试 请勿下载专题09立体几何与空间向量(第二部分)(已下线)五年北京专题06立体几何与空间向量(已下线)三年北京专题06立体几何与空间向量专题06空间向量与立体几何(成品)第一章 空间向量与立体几何 (单元测)(已下线)2023年北京高考数学真题变式题16-21甘肃省会宁县第四中学2022-2023学年高二下学期期末考试数学试题(已下线)第11讲 用空间向量研究距离、夹角问题11种常见考法归类-【暑假自学课】2023年新高二数学暑假精品课(人教A版2019选择性必修第一册)广西南宁市第二中学2023-2024学年高二上学期第一次适应性测试数学试题(已下线)第三章 空间向量与立体几何(综合提升检测卷)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)黑龙江省肇东市第四中学校2023-2024学年高二上学期第一次月考数学试题(已下线)上海市华东师范大学第二附属中学2024届高三上学期期中数学试题天津市第二南开学校2023-2024学年高三上学期期中数学试题海南省海口市琼山华侨中学2023-2024学年高二上学期期中考试数学试题(已下线)第05讲 空间向量及其应用(练习)福建省福州市(华侨、金山、教院附中等八校)2023-2024学年高二上学期期中联考数学试题新疆阿克苏地区库车市第二中学2023-2024学年高二上学期第一次月数学试题(已下线)考点12 空间角 2024届高考数学考点总动员 【讲】湖南省长沙市长郡中学2024届高三上学期月考数学试题(五)(已下线)专题01 空间向量及其应用常考题型归纳(2)上海市曹杨第二中学2023-2024学年高二上学期期末考试数学试题(已下线)专题05用空间向量研究距离、夹角问题(2个知识点6种题型1个易错点1种高考考法)(2)(已下线)专题15 立体几何解答题全归类(9大核心考点)(讲义)-1(已下线)重难点12 立体几何必考经典解答题全归类【九大题型】(已下线)通关练05 空间向量与立体几何近五年高考真题4考点精练(30题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)云南省文山州广南县第十中学校2023-2024学年高二下学期3月月考数学试题(已下线)专题23 立体几何解答题(理科)-2专题07立体几何与空间向量
10 . 设 ,函数
,函数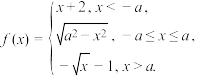 ,给出下列四个结论:
,给出下列四个结论:
① 在区间
在区间 上单调递减;
上单调递减;
②当 时,
时, 存在最大值;
存在最大值;
③设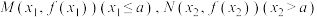 ,则
,则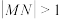 ;
;
④设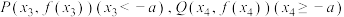 .若
.若 存在最小值,则a的取值范围是
存在最小值,则a的取值范围是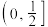 .
.
其中所有正确结论的序号是____________ .
 ,函数
,函数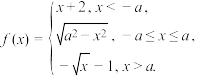 ,给出下列四个结论:
,给出下列四个结论:①
 在区间
在区间 上单调递减;
上单调递减;②当
 时,
时, 存在最大值;
存在最大值;③设
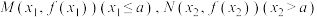 ,则
,则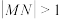 ;
;④设
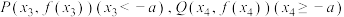 .若
.若 存在最小值,则a的取值范围是
存在最小值,则a的取值范围是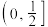 .
.其中所有正确结论的序号是
您最近一年使用:0次
2023-06-19更新
|
11150次组卷
|
23卷引用:2023年北京高考数学真题
2023年北京高考数学真题北京十年真题专题02函数概念与基本初等函数北京市西城区北师大二附中2024届高三上学期期中数学试题(已下线)高考数学测试 请勿下载专题12平面解析几何(第二部分)(已下线)五年北京专题08平面解析几何(已下线)三年北京专题08平面解析几何专题02函数与导数(成品)专题07平面解析几何(成品)(已下线)2023年北京高考数学真题变式题11-15(已下线)考点2 分段函数 2024届高考数学考点总动员 (讲)(已下线)第07讲 函数与方程(练习)(已下线)第一讲:数形结合思想【练】(已下线)专题2 函数的性质综合应用【练】 模块3 变量关系篇(函数)高三清北学霸150分晋级必备(已下线)技巧02 填空题的答题技巧(8大核心考点)(讲义)(已下线)专题05 函数的概念及表示(已下线)高三数学考前冲刺押题模拟卷01(2024新题型)(已下线)2.1 函数的概念及其表示(高考真题素材之十年高考)(已下线)2.4函数的图象(高考真题素材之十年高考)(已下线)【类题归纳】代数表达 数形结合(已下线)专题3 函数填空题(文科)-1(已下线)专题03 函数填空题(理科)-1专题08平面解析几何



