名校
1 . 已知 是定义在
是定义在 上的偶函数,当
上的偶函数,当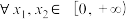 ,且
,且 时,
时,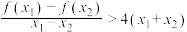 恒成立,
恒成立,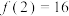 ,则满足
,则满足 的
的 的取值范围为
的取值范围为______ .
 是定义在
是定义在 上的偶函数,当
上的偶函数,当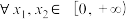 ,且
,且 时,
时,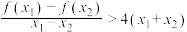 恒成立,
恒成立,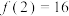 ,则满足
,则满足 的
的 的取值范围为
的取值范围为
您最近一年使用:0次
解题方法
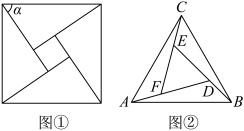
2 . 赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”.(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成,如图①),类比“赵爽弦图”,可构造如图②所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形,其中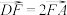 ,则
,则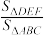 的值为
的值为______ ;设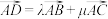 ,则
,则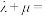
______ .
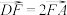 ,则
,则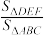 的值为
的值为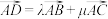 ,则
,则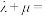
您最近一年使用:0次
3 . 复平面上两个点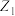 ,
,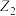 分别对应两个复数
分别对应两个复数 ,
,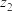 ,它们满足下列两个条件:①
,它们满足下列两个条件:①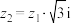 ;②两点
;②两点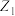 ,
,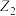 连线的中点对应的复数为
连线的中点对应的复数为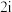 ,若
,若 为坐标原点,则
为坐标原点,则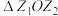 的面积为
的面积为______ .
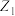 ,
,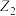 分别对应两个复数
分别对应两个复数 ,
,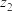 ,它们满足下列两个条件:①
,它们满足下列两个条件:①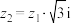 ;②两点
;②两点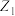 ,
,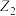 连线的中点对应的复数为
连线的中点对应的复数为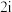 ,若
,若 为坐标原点,则
为坐标原点,则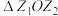 的面积为
的面积为
您最近一年使用:0次
名校
解题方法
4 . 在 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,则
,则 的取值范围是
的取值范围是______ .
 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,则
,则 的取值范围是
的取值范围是
您最近一年使用:0次
昨日更新
|
696次组卷
|
4卷引用:江苏省连云港市新海高级中学2023-2024学年高一下学期期中考试数学试卷
江苏省连云港市新海高级中学2023-2024学年高一下学期期中考试数学试卷湖北省黄冈市浠水县第一中学2023-2024学年高一下学期期末质量检测数学试题(已下线)专题4 解三角形中的最值与范围问题【练】(高一期末压轴专项)(已下线)【高一模块一】难度3 小题强化限时晋级练(基础3)
名校
解题方法
5 . 已知函数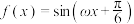 ,
,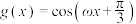 ,
, .当
.当 时,
时, 的图象至少向右移动
的图象至少向右移动________ 个单位长度可以得到 的图象;若
的图象;若 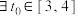 使
使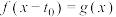 对
对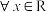 恒成立,则
恒成立,则 的最小值为
的最小值为________ .
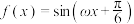 ,
,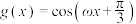 ,
, .当
.当 时,
时, 的图象至少向右移动
的图象至少向右移动 的图象;若
的图象;若 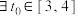 使
使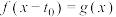 对
对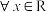 恒成立,则
恒成立,则 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
6 . 在边长为4的正方形ABCD中,如图甲所示,E,F,M分别为BC,CD,BE的中点,分别沿AE,AF及EF所在直线把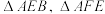 和
和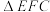 折起,使B,C,D三点重合于点P,得到三棱锥
折起,使B,C,D三点重合于点P,得到三棱锥 ,如图乙所示,则三棱锥
,如图乙所示,则三棱锥 外接球的体积是
外接球的体积是____________ ;过点M的平面截三棱锥 外接球所得截面的面积的取值范围是
外接球所得截面的面积的取值范围是____________ .
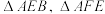 和
和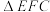 折起,使B,C,D三点重合于点P,得到三棱锥
折起,使B,C,D三点重合于点P,得到三棱锥 ,如图乙所示,则三棱锥
,如图乙所示,则三棱锥 外接球的体积是
外接球的体积是 外接球所得截面的面积的取值范围是
外接球所得截面的面积的取值范围是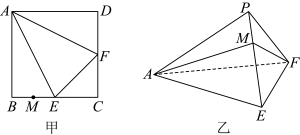
您最近一年使用:0次
名校
解题方法
7 . 已知 的面积为9,
的面积为9, ,过D分别作
,过D分别作 于E,
于E, 于F,且
于F,且 ,则
,则
______ .
 的面积为9,
的面积为9, ,过D分别作
,过D分别作 于E,
于E, 于F,且
于F,且 ,则
,则
您最近一年使用:0次
名校
解题方法
8 . 在长方形 中,
中,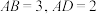 ,点E在线段AB上,
,点E在线段AB上,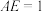 ,沿
,沿 将
将 折起,使得
折起,使得 ,此时四棱锥
,此时四棱锥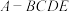 的体积为
的体积为________ .
 中,
中,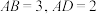 ,点E在线段AB上,
,点E在线段AB上,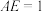 ,沿
,沿 将
将 折起,使得
折起,使得 ,此时四棱锥
,此时四棱锥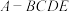 的体积为
的体积为
您最近一年使用:0次
7日内更新
|
359次组卷
|
3卷引用:湖南省郴州市第一中学等校2023-2024学年高一下学期5月联考数学试题
9 . 我国南北朝的伟大科学教祖暅于5世纪提出了著名的祖暅原理,意思就是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个几截面的面积总相等,那么这两个几何体的体积相等.如图1,为了求半球的体积,可以构造一个底面半径和高都与半球的半径相等的圆柱,与半球放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一个新几何体,用任何一个平行底面的平面去截它们时,两个截面面积总相等.如图2,某个清代陶瓷容器的上、下底面为互相平行的圆面(上底面开口,下底面封闭),侧面为球面的一部分,上、下底面圆半径都为6cm,且它们的距离为24cm,则该容器的容积为______ 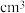 (容器的厚度忽略不计).
(容器的厚度忽略不计).
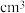 (容器的厚度忽略不计).
(容器的厚度忽略不计).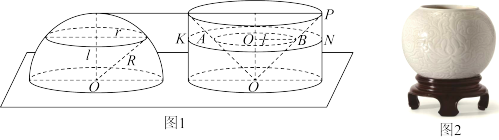
您最近一年使用:0次
名校
解题方法
10 . 如图所示,在边长为3的等边三角形 中,
中,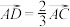 ,且点P在以
,且点P在以 的中点O为圆心、
的中点O为圆心、 为半径的半圆上,若
为半径的半圆上,若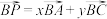 ,则下列说法正确的是
,则下列说法正确的是____________ .
① ②
② 的最大值为
的最大值为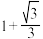
③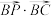 最大值为9 ④
最大值为9 ④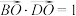
 中,
中,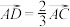 ,且点P在以
,且点P在以 的中点O为圆心、
的中点O为圆心、 为半径的半圆上,若
为半径的半圆上,若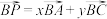 ,则下列说法正确的是
,则下列说法正确的是①
 ②
② 的最大值为
的最大值为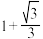
③
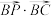 最大值为9 ④
最大值为9 ④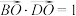

您最近一年使用:0次



