名校
解题方法
1 . 已知定义在 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有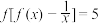 .若函数
.若函数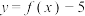 的零点个数为有限的n(n∈N)个,则n的最大值是( )
的零点个数为有限的n(n∈N)个,则n的最大值是( )
 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有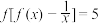 .若函数
.若函数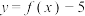 的零点个数为有限的n(n∈N)个,则n的最大值是( )
的零点个数为有限的n(n∈N)个,则n的最大值是( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
名校
2 . 已知 ,对关于
,对关于 的方程
的方程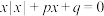 的实数解情况进行讨论,下面的结论中错误的是( )
的实数解情况进行讨论,下面的结论中错误的是( )
 ,对关于
,对关于 的方程
的方程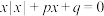 的实数解情况进行讨论,下面的结论中错误的是( )
的实数解情况进行讨论,下面的结论中错误的是( )| A.至多有三个实根 |
| B.至少有一个实根 |
C.当且仅当 时有实根 时有实根 |
D.存在 ,使原方程有三个实根 ,使原方程有三个实根 |
您最近一年使用:0次
名校
3 . 当 时,方程
时,方程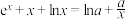 在
在 上根的个数为( )
上根的个数为( )
 时,方程
时,方程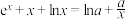 在
在 上根的个数为( )
上根的个数为( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2024-09-23更新
|
664次组卷
|
3卷引用:上海市嘉定区第一中学2024-2025学年高三上学期数学测试卷三
4 . 已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且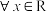 ,都有
,都有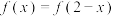 ,当
,当 时,
时, ,则函数
,则函数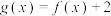 在区间
在区间 内所有零点之和为
内所有零点之和为______ .
 是定义在
是定义在 上的奇函数,且
上的奇函数,且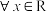 ,都有
,都有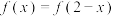 ,当
,当 时,
时, ,则函数
,则函数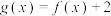 在区间
在区间 内所有零点之和为
内所有零点之和为
您最近一年使用:0次
2024-09-04更新
|
947次组卷
|
4卷引用:上海市南洋模范中学2024-2025学年高三上学期开学考试数学试卷
名校
解题方法
5 . 如图,在区间 上,曲线
上,曲线 与
与 轴围成的阴影部分面积记为面积
轴围成的阴影部分面积记为面积 ,若
,若 (
(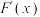 为函数
为函数 的导函数),则
的导函数),则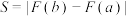 .设函数
.设函数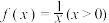
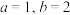 ,求
,求 的值;
的值;
(2)已知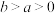 ,点
,点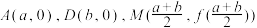 ,过点
,过点 的直线分别交
的直线分别交 于
于 两点(
两点( 在第一象限),设四边形
在第一象限),设四边形 的面积为
的面积为 ,写出
,写出 的表达式(用
的表达式(用 表示)并证明:
表示)并证明: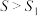 :
:
(3)函数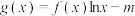 有两个不同的零点
有两个不同的零点 ,比较
,比较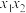 与
与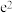 的大小,并说明理由.
的大小,并说明理由.
 上,曲线
上,曲线 与
与 轴围成的阴影部分面积记为面积
轴围成的阴影部分面积记为面积 ,若
,若 (
(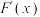 为函数
为函数 的导函数),则
的导函数),则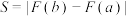 .设函数
.设函数

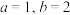 ,求
,求 的值;
的值;(2)已知
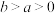 ,点
,点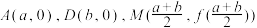 ,过点
,过点 的直线分别交
的直线分别交 于
于 两点(
两点( 在第一象限),设四边形
在第一象限),设四边形 的面积为
的面积为 ,写出
,写出 的表达式(用
的表达式(用 表示)并证明:
表示)并证明: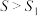 :
:(3)函数
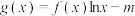 有两个不同的零点
有两个不同的零点 ,比较
,比较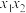 与
与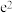 的大小,并说明理由.
的大小,并说明理由.
您最近一年使用:0次
2024-08-17更新
|
248次组卷
|
3卷引用:上海市宜川中学2024-2025学年高三上学期数学阶段测试数学试卷
名校
6 . 已知抛物线 ,a,b,c均为整数,记
,a,b,c均为整数,记 ,若
,若 均为奇数,则
均为奇数,则 有
有______ 个整数解.
 ,a,b,c均为整数,记
,a,b,c均为整数,记 ,若
,若 均为奇数,则
均为奇数,则 有
有
您最近一年使用:0次
名校
解题方法
7 . 设 ,若定义域为
,若定义域为 的函数
的函数 的图象关于直线
的图象关于直线 、直线
、直线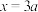 、直线
、直线 都成轴对称,且
都成轴对称,且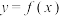 在区间
在区间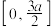 上恰有5个零点,则
上恰有5个零点,则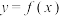 在区间
在区间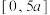 上的零点个数的最小值是
上的零点个数的最小值是______ .
 ,若定义域为
,若定义域为 的函数
的函数 的图象关于直线
的图象关于直线 、直线
、直线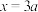 、直线
、直线 都成轴对称,且
都成轴对称,且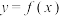 在区间
在区间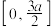 上恰有5个零点,则
上恰有5个零点,则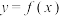 在区间
在区间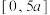 上的零点个数的最小值是
上的零点个数的最小值是
您最近一年使用:0次
解题方法
8 . 已知函数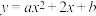 ,其中系数a、
,其中系数a、 ,任取一个函数有零点的概率是
,任取一个函数有零点的概率是________ .
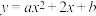 ,其中系数a、
,其中系数a、 ,任取一个函数有零点的概率是
,任取一个函数有零点的概率是
您最近一年使用:0次
2024-08-03更新
|
186次组卷
|
3卷引用:【课堂例】12.2.2 等可能性(续) 课堂例题 沪教版(2020)必修第三册第12章 概率初步
名校
9 . 设函数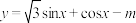 在
在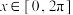 上恰有两个零点
上恰有两个零点 ,则
,则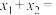
__________ .
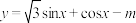 在
在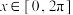 上恰有两个零点
上恰有两个零点 ,则
,则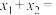
您最近一年使用:0次
2024-07-29更新
|
1068次组卷
|
5卷引用:上海市古美高级中学2023-2024学年高一下学期期末考试数学试卷
解题方法
10 . 已知函数 ,其中
,其中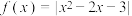 .
. 的零点;
的零点;
(2)讨论关于x的方程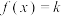 的解的个数;
的解的个数;
(3)若方程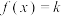 有四个不同的根
有四个不同的根 ,
, ,
, ,
, ,直接写出这四个根的和.
,直接写出这四个根的和.
 ,其中
,其中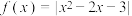 .
.
 的零点;
的零点;(2)讨论关于x的方程
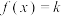 的解的个数;
的解的个数;(3)若方程
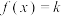 有四个不同的根
有四个不同的根 ,
, ,
, ,
, ,直接写出这四个根的和.
,直接写出这四个根的和.
您最近一年使用:0次



