名校
1 . 已知函数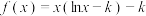
(1)讨论函数 在
在 上的单调性;
上的单调性;
(2)若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
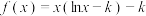
(1)讨论函数
 在
在 上的单调性;
上的单调性;(2)若函数
 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
2 . 已知函数 .
.
(1)若曲线 在点
在点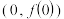 处的切线方程为
处的切线方程为 ,判断当
,判断当 时函数
时函数 的单调性;
的单调性;
(2)当 时,
时,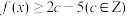 在
在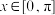 恒成立,求
恒成立,求 的最大值.
的最大值.
 .
.(1)若曲线
 在点
在点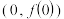 处的切线方程为
处的切线方程为 ,判断当
,判断当 时函数
时函数 的单调性;
的单调性;(2)当
 时,
时,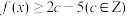 在
在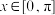 恒成立,求
恒成立,求 的最大值.
的最大值.
您最近一年使用:0次
3 . 已知函数 .
.
(1)求 在
在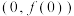 处的切线方程;
处的切线方程;
(2)求证:当 时,函数
时,函数 有且仅有
有且仅有 个零点.
个零点.
 .
.(1)求
 在
在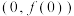 处的切线方程;
处的切线方程;(2)求证:当
 时,函数
时,函数 有且仅有
有且仅有 个零点.
个零点.
您最近一年使用:0次
2023·全国·模拟预测
名校
4 . 已知实数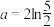 ,
,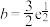 ,
,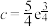 (
( 为自然对数的底数),则( )
为自然对数的底数),则( )
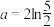 ,
,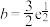 ,
,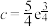 (
( 为自然对数的底数),则( )
为自然对数的底数),则( )A.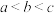 | B.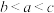 |
C. | D. |
您最近一年使用:0次
5 . 定义在 上的奇函数
上的奇函数 ,当
,当 时,
时, ,则下列选项正确的有( )
,则下列选项正确的有( )
 上的奇函数
上的奇函数 ,当
,当 时,
时, ,则下列选项正确的有( )
,则下列选项正确的有( )A. |
B. 在点 在点 处的切线方程是 处的切线方程是 |
C. 在 在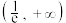 上递减 上递减 |
D.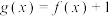 在 在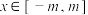 上最大值与最小值的和为2 上最大值与最小值的和为2 |
您最近一年使用:0次
名校
6 . 已知函数 ,若
,若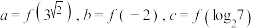 ,则
,则 的大小关系是( )
的大小关系是( )
 ,若
,若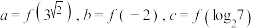 ,则
,则 的大小关系是( )
的大小关系是( )A.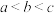 | B. |
C.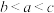 | D.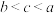 |
您最近一年使用:0次
名校
7 . 已知 ,
,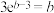 ,
, ,其中
,其中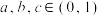 ,则( )
,则( )
 ,
,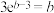 ,
, ,其中
,其中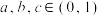 ,则( )
,则( )A. | B. | C.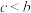 | D. |
您最近一年使用:0次
名校
8 . 已知函数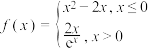 ,若关于
,若关于 的方程
的方程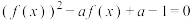 恰有四个不同的实数根,则实数
恰有四个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
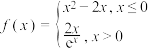 ,若关于
,若关于 的方程
的方程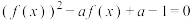 恰有四个不同的实数根,则实数
恰有四个不同的实数根,则实数 的取值范围是( )
的取值范围是( )A. | B.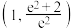 | C.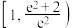 | D.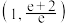 |
您最近一年使用:0次
2024-04-26更新
|
687次组卷
|
10卷引用:福建省莆田第十五中学2022-2023学年高二下学期期中测试数学试题
福建省莆田第十五中学2022-2023学年高二下学期期中测试数学试题江西省八所重点中学2022届高三4月联考数学(文)试题江西省赣州市六校联考2021-2022学年高二下学期期中数学(理)试题福建省华安县第一中学2022-2023学年高二下学期期中考试数学试题福建省宁德市霞浦县宏翔高级中学2022-2023学年高二下学期第一次段考数学试题广东省东莞市三校2023-2024学年高二下学期4月期中联考数学试题(已下线)模块2专题8零点问题 方程图象练广东省东莞市光明中学2023-2024学年高二下学期期中考试数学试卷(已下线)5.3.2函数的极值与最大(小)值(3)重庆市重庆市长寿区重庆市长寿川维中学校2023-2024学年高二下学期5月月考数学试题
名校
9 . 设函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若对于任意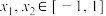 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若对于任意
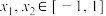 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
10 . 已知 是函数
是函数 的导函数,若函数
的导函数,若函数 的图象大致如图所示,则
的图象大致如图所示,则 的极大值点为( )
的极大值点为( )
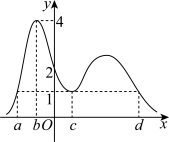
 是函数
是函数 的导函数,若函数
的导函数,若函数 的图象大致如图所示,则
的图象大致如图所示,则 的极大值点为( )
的极大值点为( )
A. | B. | C. | D. |
您最近一年使用:0次
2023-11-23更新
|
849次组卷
|
10卷引用:福建省莆田市第二十五中学2023-2024学年高三上学期月考(四)数学试卷
福建省莆田市第二十五中学2023-2024学年高三上学期月考(四)数学试卷四川省雅安市雅安市联考2023-2024学年高三上学期期中考试数学(理)试题四川省绵阳市绵阳实验高级中学2024届高三上学期11月月考数学(文)试题四川省绵阳市绵阳实验高级中学2024届高三上学期11月月考数学(理)试题陕西省商洛市多校2023-2024学年高三上学期11月联考数学(理科)试题广西普通高中2024届高三跨市联合适应性训练检测卷数学试题四川省雅安市联考2024届高三上学期期中数学(文)试题广西桂林、柳州、贺州、崇左四市2024届高三上学期跨市联合适应性检测数学试题四川省广安第二中学校2023-2024学年高三上学期第二次月考理科数学试题陕西省西安铁一中滨河高级中学2023-2024学年高二上学期第二次月考数学试题



