1 . 有四个命题,其中正确命题有( )
A.函数 是最小正周期为 是最小正周期为 的周期函数 的周期函数 |
B.锐角 中 中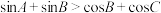 恒成立 恒成立 |
C.函数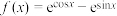 在区间 在区间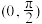 上是增函数 上是增函数 |
D.若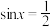 ,则 ,则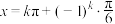 , ,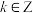 . . |
您最近一年使用:0次
2 . 已知下列命题
①函数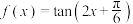 的定义域为
的定义域为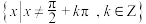 ;
;
②函数 与
与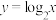 的图象关于直线
的图象关于直线 对称;
对称;
③若函数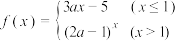 是
是 上的单调递增函数,则
上的单调递增函数,则 ;
;
④函数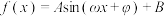 (其中
(其中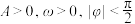 )的一部分图象如图所示,则
)的一部分图象如图所示,则 .
.
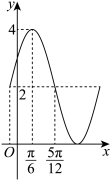
其中正确命题的序号为__________ .
①函数
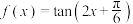 的定义域为
的定义域为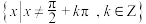 ;
;②函数
 与
与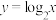 的图象关于直线
的图象关于直线 对称;
对称;③若函数
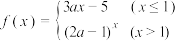 是
是 上的单调递增函数,则
上的单调递增函数,则 ;
;④函数
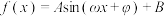 (其中
(其中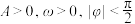 )的一部分图象如图所示,则
)的一部分图象如图所示,则 .
.
其中正确命题的序号为
您最近一年使用:0次
名校
解题方法
3 . 若 ,对于
,对于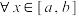 恒有
恒有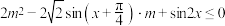 ,则
,则 的最大值是( )
的最大值是( )
 ,对于
,对于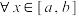 恒有
恒有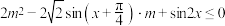 ,则
,则 的最大值是( )
的最大值是( )A.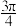 | B. | C. | D. |
您最近一年使用:0次
2023-06-11更新
|
540次组卷
|
3卷引用:广东省深圳外国语学校2023届高三上学期第一次月考(入学测试)数学试题
名校
4 . 设 ,若在区间
,若在区间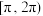 上存在a,b且
上存在a,b且 ,使得
,使得 ,则下列所给的值中
,则下列所给的值中 只可能是( )
只可能是( )
 ,若在区间
,若在区间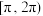 上存在a,b且
上存在a,b且 ,使得
,使得 ,则下列所给的值中
,则下列所给的值中 只可能是( )
只可能是( )A. | B.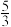 | C.2 | D.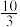 |
您最近一年使用:0次
2023-04-13更新
|
751次组卷
|
4卷引用:湖北省孝感方子高级中学2022-2023学年高一上学期12月月考数学试题
名校
5 . 2022年夏天,重庆连续出现45度的极端高温天气,打破了历史最高气温记录.根据《高温酷暑工作规定》:当日高温达到40度以上,停止当日户外露天作业.如图,8月某一天从6时~14时的温度变化曲线近似满足函数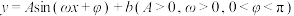 ,则下列判断正确的是( )
,则下列判断正确的是( )
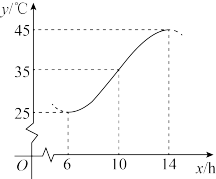
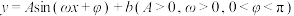 ,则下列判断正确的是( )
,则下列判断正确的是( )
| A.该函数的周期是16 |
B.该函数图象的一个对称中心为 |
C.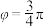 |
D.根据该函数模型进行模拟估计,当天的6时~20时,按照规定将停止户外露天工作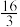 个小时 个小时 |
您最近一年使用:0次
6 . 下列结论中正确的有( )
A.若 ,则 ,则 |
B.函数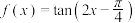 的定义域为 的定义域为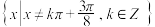 |
C.若命题“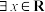 , ,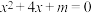 ”为假命题,则实数m的取值范围是 ”为假命题,则实数m的取值范围是 |
D.当 时, 时,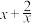 的最小值为 的最小值为 |
您最近一年使用:0次
7 . 已知定义域为 的函数
的函数 ,
, 的最小正周期均为
的最小正周期均为 ,且
,且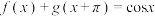 ,
,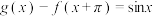 ,则( )
,则( )
 的函数
的函数 ,
, 的最小正周期均为
的最小正周期均为 ,且
,且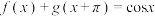 ,
,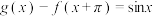 ,则( )
,则( )A. | B.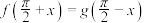 |
C.函数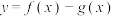 是偶函数 是偶函数 | D.函数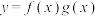 的最大值是 的最大值是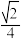 |
您最近一年使用:0次
2022-12-26更新
|
1260次组卷
|
5卷引用:2022年9月《浙江省新高考研究卷》(全国I卷)数学试题(五)
2022年9月《浙江省新高考研究卷》(全国I卷)数学试题(五)(已下线)模块四 三角函数、平面向量与解三角形-3江苏省常州市戚墅堰高级中学2023届高三二模模拟数学试题专题03函数的概念与基本初等函数专题09三角函数(2)
名校
8 . 给出的下列选项中,正确的是( )
A.函数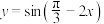 的单调递增区间为 的单调递增区间为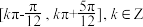 |
B.将函数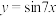 的图象向右平移 的图象向右平移 个单位,将得到 个单位,将得到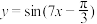 的图象 的图象 |
C.函数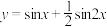 在 在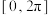 上有3个零点 上有3个零点 |
D.函数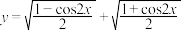 最小正周期为 最小正周期为 |
您最近一年使用:0次
2022-12-18更新
|
453次组卷
|
2卷引用:山东省百校大联考2022-2023学年高三上学期12月数学试题
解题方法
9 . 设函数 ,有下列命题:
,有下列命题:
①函数 的最小正周期为
的最小正周期为 ;
;
②对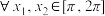 ,
,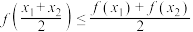 ;
;
③函数 共有5个零点;
共有5个零点;
④设 ,
,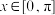 ,函数
,函数 在点
在点 处取得极大值,点
处取得极大值,点 为
为 上一点,
上一点, 为坐标原点,则
为坐标原点,则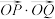 的最大值大于
的最大值大于 .
.
其中真命题的个数为( )
 ,有下列命题:
,有下列命题:①函数
 的最小正周期为
的最小正周期为 ;
;②对
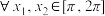 ,
,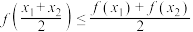 ;
;③函数
 共有5个零点;
共有5个零点;④设
 ,
,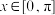 ,函数
,函数 在点
在点 处取得极大值,点
处取得极大值,点 为
为 上一点,
上一点, 为坐标原点,则
为坐标原点,则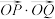 的最大值大于
的最大值大于 .
.其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
名校
解题方法
10 . 下列结论正确的是( )
A.若 ,则 ,则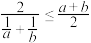 |
B.函数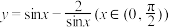 的最小值为 的最小值为 |
C.函数 的值域为 的值域为 ,则实数m的取值范围是 ,则实数m的取值范围是 |
D.若函数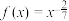 ,则 ,则 在区间 在区间 上单调递增. 上单调递增. |
您最近一年使用:0次
2022-12-15更新
|
959次组卷
|
4卷引用:重庆市西南大学附属中学校2022-2023学年高一上学期期末数学试题



