名校
1 . 如图,在棱长为2的正方体 中,P为线段
中,P为线段 的中点,Q为线段
的中点,Q为线段 上的动点,则下列结论正确的是( )
上的动点,则下列结论正确的是( )
 中,P为线段
中,P为线段 的中点,Q为线段
的中点,Q为线段 上的动点,则下列结论正确的是( )
上的动点,则下列结论正确的是( )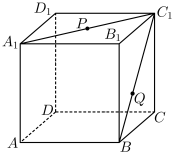
A.存在点Q,使得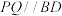 | B.存在点Q,使得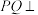 平面 平面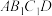 |
C.三棱锥 的体积是定值 的体积是定值 | D.存在点Q,使得PQ与AD所成的角为 |
您最近一年使用:0次
2023-05-05更新
|
2812次组卷
|
14卷引用:北京市房山区2023-2024学年高二上学期期末考试数学试卷
北京市房山区2023-2024学年高二上学期期末考试数学试卷(已下线)空间向量与立体几何(已下线)思想01 运用分类讨论的思想方法解题(5大核心考点)(讲义)北京市第二中学2023-2024学年高二下学期学段考试数学试卷北京市朝阳区2023届高三二模数学试题北京卷专题19B空间向量与立体几何(选择填空题)江西省南昌市八一中学2023届高三三模文科数学试题(已下线)高二上学期期中复习【第一章 空间向量与立体几何】十大题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)北京市人大附中2023-2024学年高二上学期期中数学试题广东省佛山市顺德德胜学校2023-2024学年高二上学期期中数学试题四川省成都市龙泉驿区东竞高级中学2023-2024学年高二上学期期中数学试题北京市海淀区人大附中2023-2024学年高二上学期期中练习数学试题辽宁省沈阳市东北育才学校2023-2024学年高二上学期第二次月考数学试题广东省佛山市南海区第一中学2023-2024高二上学期第三次大测数学试卷
解题方法
2 . 已知四面体 的各个面均为全等的等腰三角形,且
的各个面均为全等的等腰三角形,且 .设
.设 为空间内任一点,且
为空间内任一点,且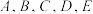 五点在同一个球面上,则( )
五点在同一个球面上,则( )
 的各个面均为全等的等腰三角形,且
的各个面均为全等的等腰三角形,且 .设
.设 为空间内任一点,且
为空间内任一点,且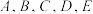 五点在同一个球面上,则( )
五点在同一个球面上,则( )A. |
B.四面体 的体积为 的体积为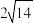 |
C.当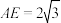 时,点 时,点 的轨迹长度为 的轨迹长度为 |
D.当三棱锥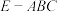 的体积为 的体积为 时,点 时,点 的轨迹长度为 的轨迹长度为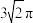 |
您最近一年使用:0次
2024-02-24更新
|
2481次组卷
|
7卷引用:黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题
黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题(已下线)第1套 复盘提升卷(模块二 2月开学)(已下线)黄金卷06(2024新题型)(已下线)专题04 立体几何(已下线)压轴小题7 探究立体几何中的动态问题(已下线)第20题 立体几何中的轨迹问题(高三二轮每日一题)广西梧州市、忻城县2024届高中毕业班5月仿真考试数学试卷
名校
解题方法
3 . 如图,在棱长为1的正方体 中,E,F分别为棱
中,E,F分别为棱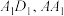 的中点,G为线段
的中点,G为线段 上一个动点,则( )
上一个动点,则( )
 中,E,F分别为棱
中,E,F分别为棱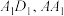 的中点,G为线段
的中点,G为线段 上一个动点,则( )
上一个动点,则( )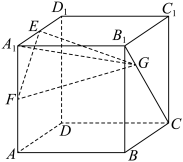
A.存在点G,使直线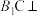 平面 平面 |
B.存在点G,使平面 ∥平面 ∥平面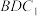 |
C.三棱锥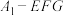 的体积为定值 的体积为定值 |
D.平面 截正方体所得截面的最大面积为 截正方体所得截面的最大面积为 |
您最近一年使用:0次
2023-05-08更新
|
2713次组卷
|
9卷引用:广东省麻涌,塘厦,七中,济川四校2023-2024学年高一下学期5月期中联考数学试题
名校
解题方法
4 . 如图是数学家Germinal Dandelin用来证明一个平面截圆锥侧面得到的截口曲线是椭圆的模型(称为“Dandelin双球”).在圆锥内放两个大小不同的小球,使得它们分别与圆锥的侧面、截面相切,截面分别与球 ,球
,球 切于点E,F(E,F是截口椭圆C的焦点).设图中球
切于点E,F(E,F是截口椭圆C的焦点).设图中球 ,球
,球 的半径分别为4和1,球心距
的半径分别为4和1,球心距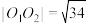 ,则( )
,则( )
 ,球
,球 切于点E,F(E,F是截口椭圆C的焦点).设图中球
切于点E,F(E,F是截口椭圆C的焦点).设图中球 ,球
,球 的半径分别为4和1,球心距
的半径分别为4和1,球心距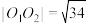 ,则( )
,则( )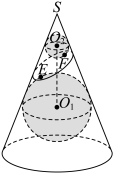
A.椭圆C的中心不在直线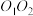 上 上 |
B.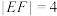 |
C.直线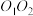 与椭圆C所在平面所成的角的正弦值为 与椭圆C所在平面所成的角的正弦值为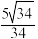 |
D.椭圆C的离心率为 |
您最近一年使用:0次
2024-03-03更新
|
2453次组卷
|
3卷引用:山东省日照市2024届高三下学期一模数学试题
名校
5 . 如图,圆台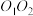 的轴截面为等腰梯形
的轴截面为等腰梯形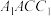 ,
,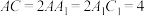 ,B为底面圆周上异于A,C的点.
,B为底面圆周上异于A,C的点.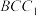 内,过
内,过 作一条直线与平面
作一条直线与平面 平行,并说明理由;
平行,并说明理由;
(2)设平面 ∩平面
∩平面 ,
, 与平面QAC所成角为
与平面QAC所成角为 ,当四棱锥
,当四棱锥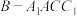 的体积最大时,求
的体积最大时,求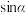 的取值范围.
的取值范围.
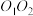 的轴截面为等腰梯形
的轴截面为等腰梯形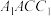 ,
,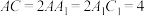 ,B为底面圆周上异于A,C的点.
,B为底面圆周上异于A,C的点.
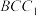 内,过
内,过 作一条直线与平面
作一条直线与平面 平行,并说明理由;
平行,并说明理由;(2)设平面
 ∩平面
∩平面 ,
, 与平面QAC所成角为
与平面QAC所成角为 ,当四棱锥
,当四棱锥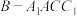 的体积最大时,求
的体积最大时,求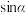 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-25更新
|
2345次组卷
|
8卷引用:安徽省合肥一六八中学等学校2024届高三上学期名校期末联合测试数学试题
名校
6 . 已知一个正四棱台的上、下底面边长分别为2,8,侧棱长为 ,则该正四棱台内半径最大的球的表面积为( )
,则该正四棱台内半径最大的球的表面积为( )
 ,则该正四棱台内半径最大的球的表面积为( )
,则该正四棱台内半径最大的球的表面积为( )A. | B.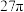 | C.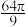 | D.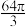 |
您最近一年使用:0次
2024-05-13更新
|
2055次组卷
|
6卷引用:江苏省南通、扬州、泰州七市2024届高三第三次调研测试数学试题
江苏省南通、扬州、泰州七市2024届高三第三次调研测试数学试题(已下线)6.6.3 球的表面积和体积-同步精品课堂(北师大版2019必修第二册)(已下线)专题07 球与几何体的切、接及立体几何最值问题-期末考点大串讲(苏教版(2019))广东省华南师范大学附属中学2024届高三下学期模拟测试(一)数学试题2024届湖南省衡阳市雁峰区衡阳市第八中学高三模拟预测数学试题广东省广州市广雅中学2024届高三下学期教学情况检测(三)数学试题
名校
解题方法
7 . 已知正四棱柱 的体积为16,
的体积为16, 是棱
是棱 的中点,
的中点, 是侧棱
是侧棱 上的动点,直线
上的动点,直线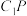 交平面
交平面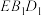 于点
于点 ,则动点
,则动点 的轨迹长度的最小值为
的轨迹长度的最小值为______ .
 的体积为16,
的体积为16, 是棱
是棱 的中点,
的中点, 是侧棱
是侧棱 上的动点,直线
上的动点,直线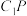 交平面
交平面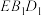 于点
于点 ,则动点
,则动点 的轨迹长度的最小值为
的轨迹长度的最小值为
您最近一年使用:0次
2023-03-24更新
|
2195次组卷
|
11卷引用:重难点突破04 立体几何中的轨迹问题(六大题型)
(已下线)重难点突破04 立体几何中的轨迹问题(六大题型)黑龙江省齐齐哈尔市龙西北高中名校联盟2023-2024学年高三上学期期末联合考试数学试题(已下线)空间几何体专题10空间中点线面的位置关系(已下线)第三章 空间轨迹问题 专题六 立体几何轨迹中的范围、最值问题 微点1 立体几何轨迹中的范围、最值问题【培优版】四川省泸州市泸县第五中学2023-2024学年高一下学期6月月考数学试题山东省聊城市2023届高三下学期第一次模拟数学试题山东省聊城市2023届高三一模数学试题专题19平面解析几何(填空题)山西省吕梁市孝义市部分学校2024届高三上学期12月月考数学试题山西省晋中市灵石县第一中学校2024届高三上学期12月月考数学试题
名校
8 . 如图,直三棱柱 中,
中, ⊥
⊥ ,
, ,
,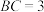 ,点P在棱
,点P在棱 上,且
上,且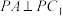 ,当
,当 的面积取最小值时,三棱锥
的面积取最小值时,三棱锥 的外接球的表面积为
的外接球的表面积为______ .
 中,
中, ⊥
⊥ ,
, ,
,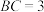 ,点P在棱
,点P在棱 上,且
上,且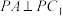 ,当
,当 的面积取最小值时,三棱锥
的面积取最小值时,三棱锥 的外接球的表面积为
的外接球的表面积为
您最近一年使用:0次
2023-01-04更新
|
2306次组卷
|
14卷引用:广东省深圳市深圳中学2024届高三上学期8月开学摸底数学试题
(已下线)广东省深圳市深圳中学2024届高三上学期8月开学摸底数学试题(已下线)空间几何体2023年普通高等学校招生全国统一考试·新高考仿真模拟卷数学(三)(已下线)河南省南阳市2022-2023学年高三上学期期末数学(理)试题变式题11-15广东省广州市协和中学2022-2023学年高二下学期2月月考数学试题(已下线)山东省济南市2022届高三二模数学试题变式题11-16上海市嘉定区2023届高三下学期2月调研数学试题海南省屯昌县2023届高三二模统考(A)数学试题(已下线)重难点专题01 空间几何体测试-【同步题型讲义】河北省唐县第一中学2022-2023学年高一下学期5月月考数学试题安徽省阜阳汇文中学2022-2023学年高一下学期第三次月考数学试题四川省达州外国语学校2023-2024学年高二上学期期中考试数学试题(已下线)重难点突破01 玩转外接球、内切球、棱切球(二十三大题型)-3(已下线)第11章 简单几何体(压轴必刷30题专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)
名校
解题方法
9 . 如图,在三棱锥 ,
, 是以AC为斜边的等腰直角三角形,且
是以AC为斜边的等腰直角三角形,且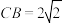 ,
,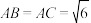 ,二面角
,二面角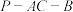 的大小为
的大小为 ,则三棱锥
,则三棱锥 的外接球表面积为( )
的外接球表面积为( )
 ,
, 是以AC为斜边的等腰直角三角形,且
是以AC为斜边的等腰直角三角形,且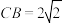 ,
,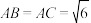 ,二面角
,二面角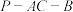 的大小为
的大小为 ,则三棱锥
,则三棱锥 的外接球表面积为( )
的外接球表面积为( )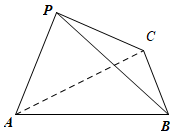
A.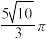 | B.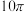 | C.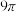 | D.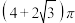 |
您最近一年使用:0次
2022-01-04更新
|
4247次组卷
|
18卷引用:专题09空间几何体的表面积与体积
专题09空间几何体的表面积与体积(已下线)专题6-1立体几何动点与外接球归类-1(已下线)专题13 一网打尽外接球、内切球与棱切球问题 (14大核心考点)(讲义)(已下线)第二章 立体几何中的计算 专题六 几何体的外接球、棱切球、内切球 微点11 二面角的四面体模型【基础版】(已下线)专题突破:立体几何外接球的常见模型-同步题型分类归纳讲与练(人教A版2019必修第二册)黑龙江省哈尔滨市第三中学2021-2022学年高三第四次验收考试数学(理科)试题(已下线)专题10 立体几何线面位置关系及空间角的计算(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题09立体几何线面位置关系及面积体积计算问题(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》广东省梅州市梅江区梅州中学、大埔县虎山中学、梅县区高级中学、丰顺县丰顺中学四校2021-2022学年高一下学期5月联考数学试题(已下线)第08讲 拓展一:空间几何体内接球与外接球问题 (讲)湖北省高中名校联合体2022-2023学年高三下学期开学诊断性考试数学试题(已下线)拓展一:空间几何体的外接球与内切球问题(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)立体几何专题:外接球问题中常见的8种模型(已下线)专题17 球面几何(外接球、内切球和棱切球)-2内蒙古包钢第一中学2022届高三一模数学(理)试题江苏省徐州市沛县2022-2023学年高一下学期第二次学情调研数学试题安徽省六安第二中学2022-2023学年高一下学期期末考试数学试题广东省东莞市东莞外国语学校2024届高三上学期第四次月考数学试题
名校
解题方法
10 . 已知空间四面体 满足
满足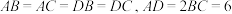 ,则该四面体外接球体积的最小值为
,则该四面体外接球体积的最小值为______ .
 满足
满足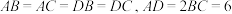 ,则该四面体外接球体积的最小值为
,则该四面体外接球体积的最小值为
您最近一年使用:0次
2024-04-05更新
|
1974次组卷
|
4卷引用:华大新高考联盟2024届高三4月教学质量测评文科数学试题(老教材全国卷)



