1 . 计算
__________ .

您最近一年使用:0次
2024-01-17更新
|
1099次组卷
|
4卷引用:吉林省通化市梅河口市第五中学2023-2024学年高一上学期期末数学试题
解题方法
2 . 已知函数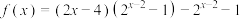 只有两个零点
只有两个零点 ,则( )
,则( )
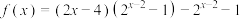 只有两个零点
只有两个零点 ,则( )
,则( )A.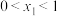 | B.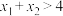 |
C.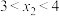 | D.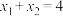 |
您最近一年使用:0次
2024-01-16更新
|
372次组卷
|
3卷引用:吉林省部分名校2023-2024学年高一上学期期末联合考试数学试题
名校
3 . 声强级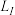 (单位:dB)由公式
(单位:dB)由公式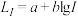 给出,其中
给出,其中 为声强(单位:
为声强(单位: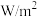 ),相应不同声的声强级如下表所示,则( )
),相应不同声的声强级如下表所示,则( )
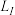 (单位:dB)由公式
(单位:dB)由公式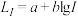 给出,其中
给出,其中 为声强(单位:
为声强(单位: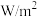 ),相应不同声的声强级如下表所示,则( )
),相应不同声的声强级如下表所示,则( ) ( (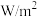 ) ) | 正常人能忍受最高声强1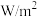 | 正常人能忍受最低声强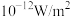 | 正常人平时谈话声强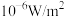 | 某人谈话声强 |
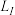 (dB) (dB) | 120 | 0 | 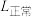 | 80 |
A.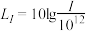 | B.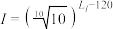 | C. | D.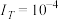 |
您最近一年使用:0次
解题方法
4 . 已知 ,
,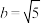 ,
,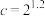 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
 ,
,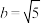 ,
,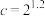 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )A.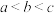 | B.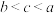 | C. | D.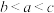 |
您最近一年使用:0次
解题方法
5 . 若指数函数 在
在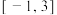 上恒有
上恒有 ,则a的最大值为
,则a的最大值为_______ .
 在
在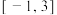 上恒有
上恒有 ,则a的最大值为
,则a的最大值为
您最近一年使用:0次
6 . 函数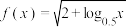 的定义域为
的定义域为________ .
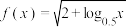 的定义域为
的定义域为
您最近一年使用:0次
名校
解题方法
7 . 已知函数 ,
, ,方程
,方程 恰有两个不相等的实数根
恰有两个不相等的实数根 (
( ),设
),设 ,则实数t的取值范围是
,则实数t的取值范围是________ .
 ,
, ,方程
,方程 恰有两个不相等的实数根
恰有两个不相等的实数根 (
( ),设
),设 ,则实数t的取值范围是
,则实数t的取值范围是
您最近一年使用:0次
解题方法
8 . 已知幂函数 满足
满足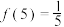 .
.
(1)求 的解析式;
的解析式;
(2)判断函数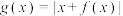 的奇偶性,并说明理由.
的奇偶性,并说明理由.
 满足
满足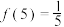 .
.(1)求
 的解析式;
的解析式;(2)判断函数
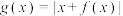 的奇偶性,并说明理由.
的奇偶性,并说明理由.
您最近一年使用:0次
2024-01-14更新
|
209次组卷
|
2卷引用:吉林省部分名校2023-2024学年高一上学期期末联合考试数学试题
名校
解题方法
9 . 已知 是自然对数的底数,
是自然对数的底数, .
.
(1)判断函数 在
在 上的单调性并证明;
上的单调性并证明;
(2)解不等式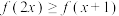 .
.
 是自然对数的底数,
是自然对数的底数, .
.(1)判断函数
 在
在 上的单调性并证明;
上的单调性并证明;(2)解不等式
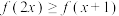 .
.
您最近一年使用:0次
2024-01-14更新
|
768次组卷
|
5卷引用:吉林省长春吉大附中实验学校2023-2024学年高一上学期期末考试数学试题
名校
10 . 已知某超市的新鲜鸡蛋存储温度x(单位:摄氏度)与保鲜时间t(单位:小时)之间的函数关系式为 该超市的新鲜鸡蛋在存储温度为8摄氏度的情况下,其保鲜时间约为432小时;在存储温度为6摄氏度的情况下,其保鲜时间约为576小时.
该超市的新鲜鸡蛋在存储温度为8摄氏度的情况下,其保鲜时间约为432小时;在存储温度为6摄氏度的情况下,其保鲜时间约为576小时.
(1)求该超市的新鲜鸡蛋在存储温度为4摄氏度的情况下,其保鲜时间约为多少小时;
(2)若该超市想要保证新鲜鸡蛋的保鲜时间不少于1024小时,则超市对新鲜鸡蛋的存储温度设置应该不高于多少摄氏度?
 该超市的新鲜鸡蛋在存储温度为8摄氏度的情况下,其保鲜时间约为432小时;在存储温度为6摄氏度的情况下,其保鲜时间约为576小时.
该超市的新鲜鸡蛋在存储温度为8摄氏度的情况下,其保鲜时间约为432小时;在存储温度为6摄氏度的情况下,其保鲜时间约为576小时.(1)求该超市的新鲜鸡蛋在存储温度为4摄氏度的情况下,其保鲜时间约为多少小时;
(2)若该超市想要保证新鲜鸡蛋的保鲜时间不少于1024小时,则超市对新鲜鸡蛋的存储温度设置应该不高于多少摄氏度?
您最近一年使用:0次
2024-01-14更新
|
153次组卷
|
3卷引用:吉林省部分名校2023-2024学年高一上学期期末联合考试数学试题



