解题方法
1 . 可利用基本不等式解决下列问题:
(1)已知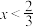 ,求函数
,求函数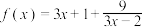 的最大值;
的最大值;
(2)已知 ,
, 且
且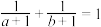 ,求
,求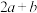 的最小值;
的最小值;
(3)已知正数a,b满足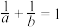 ,求
,求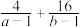 的最小值.
的最小值.
(1)已知
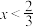 ,求函数
,求函数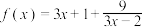 的最大值;
的最大值;(2)已知
 ,
, 且
且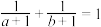 ,求
,求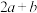 的最小值;
的最小值;(3)已知正数a,b满足
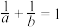 ,求
,求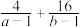 的最小值.
的最小值.
您最近一年使用:0次
昨日更新
|
209次组卷
|
2卷引用:河北省河北正中实验中学2024-2025学年高一上学期第一次月考数学试卷
名校
2 . 已知集合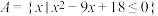 ,
,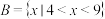 .
.
(1)分别求 ,
, .
.
(2)已知 ,且
,且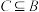 ,求实数
,求实数 的取值范围.
的取值范围.
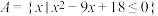 ,
,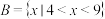 .
.(1)分别求
 ,
, .
.(2)已知
 ,且
,且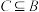 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
871次组卷
|
3卷引用:河北省承德市双滦区实验中学2024-2025学年高一上学期10月月考数学试题
名校
解题方法
3 . 已知正数 满足
满足 .
.
(1)求 的最小值;
的最小值;
(2)求 的最小值;
的最小值;
(3)求 的最小值.
的最小值.
 满足
满足 .
.(1)求
 的最小值;
的最小值;(2)求
 的最小值;
的最小值;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
7日内更新
|
490次组卷
|
2卷引用:河北省唐山市第一中学2024-2025学年高一上学期10月月考数学试题
名校
解题方法
4 . 已知关于 的不等式
的不等式 .
.
(1)若不等式的解集为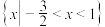 ,求实数
,求实数 的值;
的值;
(2)若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(3)在(2)的条件下,解关于x的不等式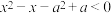 .
.
 的不等式
的不等式 .
.(1)若不等式的解集为
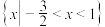 ,求实数
,求实数 的值;
的值;(2)若不等式
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(3)在(2)的条件下,解关于x的不等式
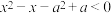 .
.
您最近一年使用:0次
名校
解题方法
5 . (1)已知 ,
,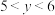 ,求
,求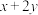 的取值范围;
的取值范围;
(2)比较两个代数式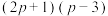 与
与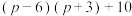 的大小.
的大小.
(3)若 2,
2,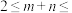 4,求4m-2n的取值范围.
4,求4m-2n的取值范围.
 ,
,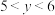 ,求
,求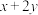 的取值范围;
的取值范围;(2)比较两个代数式
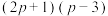 与
与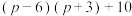 的大小.
的大小.(3)若
 2,
2,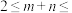 4,求4m-2n的取值范围.
4,求4m-2n的取值范围.
您最近一年使用:0次
名校
解题方法
6 . 在 中,内角A,B,C所对边分别为a,b,c,已知
中,内角A,B,C所对边分别为a,b,c,已知 .
.
(1)求角A的大小;
(2)若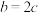 ,
, 的面积为
的面积为 ,求
,求 的周长.
的周长.
 中,内角A,B,C所对边分别为a,b,c,已知
中,内角A,B,C所对边分别为a,b,c,已知 .
.(1)求角A的大小;
(2)若
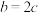 ,
, 的面积为
的面积为 ,求
,求 的周长.
的周长.
您最近一年使用:0次
7日内更新
|
1854次组卷
|
6卷引用:河北省保定市河北安国中学2024-2025学年高一下学期第一次月考数学试题
河北省保定市河北安国中学2024-2025学年高一下学期第一次月考数学试题四川省南充市2025届高三高考适应性考试(一诊)数学试卷云南省昆明市西南联大研究院附属学校2024-2025学年高二上学期10月月考数学试卷北京市陈经纶中学2025届高三上学期10月月考数学试题(已下线)考点42 余弦定理及应用 --高考数学100个黄金考点(2025届)【练】(已下线)第01章 函数与方程的思想【提升版】
7 . (1)已知 ,求
,求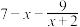 的最大值;
的最大值;
(2)已知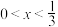 ,求
,求 的最大值.
的最大值.
 ,求
,求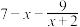 的最大值;
的最大值;(2)已知
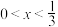 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
8 . 设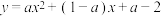 .
.
(1)若不等式 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式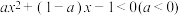 .
.
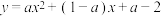 .
.(1)若不等式
 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)解关于
 的不等式
的不等式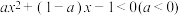 .
.
您最近一年使用:0次
名校
9 . 求下列不等式的解集:
(1)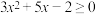 ;
;
(2) ;
;
(1)
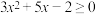 ;
;(2)
 ;
;
您最近一年使用:0次
解题方法
10 . (1)已知 ,且
,且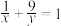 ,求
,求 的最小值.
的最小值.
(2)已知 ,求
,求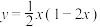 的最大值.
的最大值.
(3)已知 都是正数,若
都是正数,若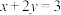 ,求
,求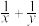 的最小值.
的最小值.
 ,且
,且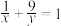 ,求
,求 的最小值.
的最小值.(2)已知
 ,求
,求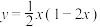 的最大值.
的最大值. (3)已知
 都是正数,若
都是正数,若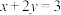 ,求
,求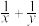 的最小值.
的最小值.
您最近一年使用:0次



