名校
解题方法
1 . 如图是一个棱长为2的正方体的展开图,其中 分别是棱
分别是棱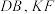 的中点.请以
的中点.请以 三点所在面为底面将展开图还原为正方体.
三点所在面为底面将展开图还原为正方体. 在平面
在平面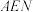 内;
内;
(2)用平面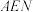 截正方体,将正方体分成两个几何体,两个几何体的体积分别为
截正方体,将正方体分成两个几何体,两个几何体的体积分别为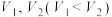 ,试判断体积较小的几何体的形状(不需要证明),并求
,试判断体积较小的几何体的形状(不需要证明),并求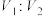 的值.
的值.
 分别是棱
分别是棱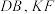 的中点.请以
的中点.请以 三点所在面为底面将展开图还原为正方体.
三点所在面为底面将展开图还原为正方体.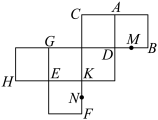
 在平面
在平面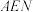 内;
内;(2)用平面
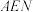 截正方体,将正方体分成两个几何体,两个几何体的体积分别为
截正方体,将正方体分成两个几何体,两个几何体的体积分别为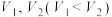 ,试判断体积较小的几何体的形状(不需要证明),并求
,试判断体积较小的几何体的形状(不需要证明),并求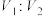 的值.
的值.
您最近一年使用:0次
2024-04-26更新
|
226次组卷
|
2卷引用:黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期期中考试数学试题
解题方法
2 . 已知函数 ,(其中
,(其中 是自然对数的底数)
是自然对数的底数)
(1)判断函数 在
在 上的单调性(不必证明);
上的单调性(不必证明);
(2)求证:函数 在
在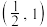 内存在零点
内存在零点 ,且
,且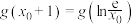 ;
;
(3)在(2)的条件下,求使不等式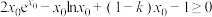 成立的整数
成立的整数 的最大值.
的最大值.
(参考数据: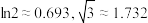 )
)
 ,(其中
,(其中 是自然对数的底数)
是自然对数的底数)(1)判断函数
 在
在 上的单调性(不必证明);
上的单调性(不必证明);(2)求证:函数
 在
在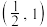 内存在零点
内存在零点 ,且
,且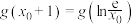 ;
;(3)在(2)的条件下,求使不等式
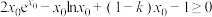 成立的整数
成立的整数 的最大值.
的最大值.(参考数据:
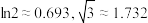 )
)
您最近一年使用:0次
名校
3 . 等腰梯形 中,
中,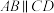 ,
, ,
,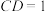 .若点
.若点 、
、 均在
均在 上,且
上,且 .如图(一)所示,沿
.如图(一)所示,沿 将
将 折起,沿
折起,沿 将
将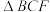 折起,使
折起,使 、
、 两点重合为
两点重合为 .
.
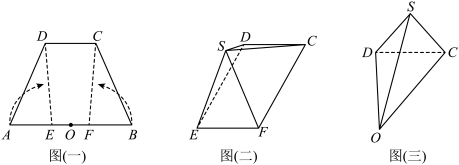
(1)若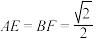 ,如图(二)所示,求证:平面
,如图(二)所示,求证:平面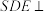 平面
平面 ;
;
(2)若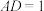 ,
, 为
为 中点,当
中点,当 与
与 重合于
重合于 时,如图(三)所示,求
时,如图(三)所示,求 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(3)请设计一个翻折方案使四棱锥 的外接球半径为
的外接球半径为 ,证明你的结论,并求此方案下的
,证明你的结论,并求此方案下的 的长度及
的长度及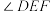 的大小.
的大小.
 中,
中,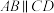 ,
, ,
,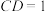 .若点
.若点 、
、 均在
均在 上,且
上,且 .如图(一)所示,沿
.如图(一)所示,沿 将
将 折起,沿
折起,沿 将
将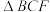 折起,使
折起,使 、
、 两点重合为
两点重合为 .
.
(1)若
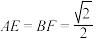 ,如图(二)所示,求证:平面
,如图(二)所示,求证:平面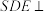 平面
平面 ;
;(2)若
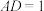 ,
, 为
为 中点,当
中点,当 与
与 重合于
重合于 时,如图(三)所示,求
时,如图(三)所示,求 与平面
与平面 所成角的余弦值;
所成角的余弦值;(3)请设计一个翻折方案使四棱锥
 的外接球半径为
的外接球半径为 ,证明你的结论,并求此方案下的
,证明你的结论,并求此方案下的 的长度及
的长度及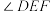 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
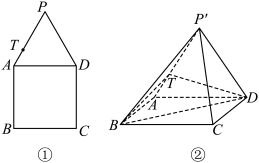
4 . 如图①所示,已知正三角形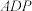 与正方形
与正方形 ,将
,将 沿
沿 翻折至
翻折至 所在的位置,连接
所在的位置,连接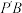 ,
,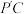 ,得到如图②所示的四棱锥.已知
,得到如图②所示的四棱锥.已知 ,
,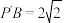 ,
, 为
为 上一点,且满足
上一点,且满足 .
.
(1)求证: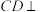 平面
平面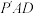 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得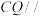 平面
平面 .若存在,指出点
.若存在,指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
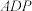 与正方形
与正方形 ,将
,将 沿
沿 翻折至
翻折至 所在的位置,连接
所在的位置,连接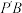 ,
,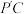 ,得到如图②所示的四棱锥.已知
,得到如图②所示的四棱锥.已知 ,
,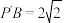 ,
, 为
为 上一点,且满足
上一点,且满足 .
.
(1)求证:
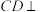 平面
平面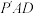 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得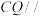 平面
平面 .若存在,指出点
.若存在,指出点 的位置,并证明你的结论;若不存在,请说明理由.
的位置,并证明你的结论;若不存在,请说明理由.
您最近一年使用:0次
2023-04-19更新
|
572次组卷
|
4卷引用:黑龙江省齐齐哈尔市第八中学校2022-2023学年高一下学期期末数学试题
黑龙江省齐齐哈尔市第八中学校2022-2023学年高一下学期期末数学试题浙江省宁波市北仑中学2022-2023学年高一下学期期中数学试题(已下线)立体几何专题:立体几何探索性问题的8种考法(已下线)13.2 基本图形位置关系(分层练习)
名校
解题方法
5 . 已知函数 的定义域是
的定义域是 ,对定义域的任意
,对定义域的任意 都有
都有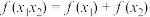 ,且当
,且当 时,
时,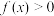 ,
,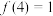 ;
;
(1)求证: ;
;
(2)试判断 在
在 的单调性并用定义证明你的结论;
的单调性并用定义证明你的结论;
(3)解不等式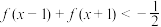
 的定义域是
的定义域是 ,对定义域的任意
,对定义域的任意 都有
都有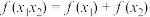 ,且当
,且当 时,
时,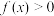 ,
,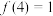 ;
;(1)求证:
 ;
;(2)试判断
 在
在 的单调性并用定义证明你的结论;
的单调性并用定义证明你的结论;(3)解不等式
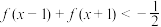
您最近一年使用:0次
2022-04-08更新
|
1891次组卷
|
5卷引用:黑龙江省绥化市第一中学2020-2021学年高一上学期期中考试数学试题
黑龙江省绥化市第一中学2020-2021学年高一上学期期中考试数学试题(已下线)第14讲 函数的单调性-【暑假自学课】2022年新高一数学暑假精品课(苏教版2019必修第一册)单调性与最大(小)值广西壮族自治区玉林市博白县中学2023-2024学年高一上学期12月月考数学试题安徽省合肥市第一中学2022-2023学年高一上学期期中教学质量检测数学试题
名校
解题方法
6 . 如图在四棱锥P - ABCD中,底面ABCD是矩形,点E,F分别是棱PC和PD的中点.
(2)若AP=AD,且平面PAD⊥平面ABCD,证明AF⊥平面PCD.
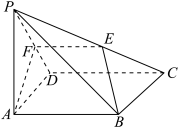
(2)若AP=AD,且平面PAD⊥平面ABCD,证明AF⊥平面PCD.
您最近一年使用:0次
2021-08-28更新
|
1655次组卷
|
12卷引用:黑龙江省鹤岗市第一中学2018-2019学年高一下学期期末数学(理)试题
黑龙江省鹤岗市第一中学2018-2019学年高一下学期期末数学(理)试题【全国百强校】江苏省涟水中学2018-2019学年高一5月月考数学试题山东省滕州市第一中学2019-2020学年高一下学期第一次月考数学试题山东省泰安市泰安实验中学2019-2020学年高一下学期数学期中考试数学试题(已下线)【新教材精创】11.4.2平面与平面垂直(第2课时)练习(1)(已下线)全册综合测试模拟三-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》(已下线)期末测试一(B卷提升篇)- 2020-2021学年高一数学必修第二册同步单元AB卷(新教材苏教版)第13章:立体几何初步 - 基本图形及位置关系(B卷提升卷)- 2020-2021学年高一数学必修第二册同步单元AB卷(新教材苏教版)(已下线)2020年秋季高二数学开学摸底考试卷(新教材人教A版)01安徽省阜阳市耀云中学2020-2021学年高二上学期期中数学试题(已下线)第十一章 立体几何初步 11.4 空间中的垂直关系 11.4.2 平面与平面垂直(已下线)FHgkyldyjsx10
名校
7 . 已知函数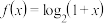 ,而函数
,而函数 的图象与
的图象与 的图象关于
的图象关于 轴对称.
轴对称.
(1)直接写出函数 的解析式;
的解析式;
(2)令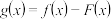 .判断函数
.判断函数 的奇偶性并证明;
的奇偶性并证明;
(3)求证:函数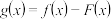 是定义域上的增函数.
是定义域上的增函数.
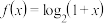 ,而函数
,而函数 的图象与
的图象与 的图象关于
的图象关于 轴对称.
轴对称.(1)直接写出函数
 的解析式;
的解析式;(2)令
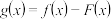 .判断函数
.判断函数 的奇偶性并证明;
的奇偶性并证明;(3)求证:函数
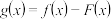 是定义域上的增函数.
是定义域上的增函数.
您最近一年使用:0次
名校
8 . 已知函数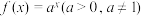 其反函数为
其反函数为
(1)求证:对任意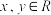 都有
都有 ,对任意
,对任意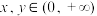 都有
都有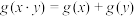
(2)令 ,讨论
,讨论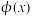 的定义域并判断其单调性(无需证明).
的定义域并判断其单调性(无需证明).
(3)当 时,求函数
时,求函数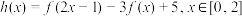 的值域;
的值域;
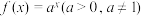 其反函数为
其反函数为
(1)求证:对任意
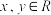 都有
都有 ,对任意
,对任意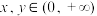 都有
都有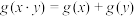
(2)令
 ,讨论
,讨论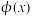 的定义域并判断其单调性(无需证明).
的定义域并判断其单调性(无需证明).(3)当
 时,求函数
时,求函数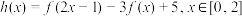 的值域;
的值域;
您最近一年使用:0次
名校
9 . 用函数单调性定义证明,求证:函数 在区间
在区间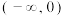 上是单调增函数
上是单调增函数
 在区间
在区间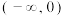 上是单调增函数
上是单调增函数
您最近一年使用:0次
2019-11-15更新
|
147次组卷
|
2卷引用:黑龙江省哈尔滨市第三中学2019-2020学年高一上学期期中数学试题(国际部)
名校
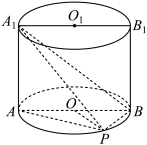
10 . 如图,已知点P在圆柱OO1的底面⊙O上,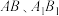 分别为⊙O、⊙O1的直径,且
分别为⊙O、⊙O1的直径,且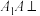 平面
平面 .
.
(1)求证: ;
;
(2)若圆柱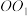 的体积
的体积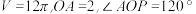 ,
,
①求三棱锥A1﹣APB的体积.
②在线段AP上是否存在一点M,使异面直线OM与 所成角的余弦值为
所成角的余弦值为 ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
 分别为⊙O、⊙O1的直径,且
分别为⊙O、⊙O1的直径,且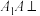 平面
平面 .
.
(1)求证:
 ;
;(2)若圆柱
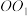 的体积
的体积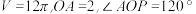 ,
,①求三棱锥A1﹣APB的体积.
②在线段AP上是否存在一点M,使异面直线OM与
 所成角的余弦值为
所成角的余弦值为 ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
您最近一年使用:0次
2019-06-19更新
|
406次组卷
|
2卷引用:黑龙江省鹤岗市第一中学2018-2019学年高一下学期期末数学(文)试题



