解题方法
1 . 为了迎接到校访问的同学,需要分上午、下午和晚上三个组各安排5名本校学生作为志愿者负责接待,并要求下午组的志愿者不能与上午组、晚上组的重复.某班共有40名学生,其中22名女生和18名男生,现准备从中选择志愿者.
(1)共有多少种选法?(不计算出具体的数字,列出式子即可)
(2)如果下午组中有一名男生请假,需要从班上的非志愿者中选一名男生替代,那么至少有多少种选法?
(3)如果三个组的志愿者都不能重复,且性别不全相同,那么共有多少种选法?(不计算出具体的数字,列出式子即可)
(1)共有多少种选法?(不计算出具体的数字,列出式子即可)
(2)如果下午组中有一名男生请假,需要从班上的非志愿者中选一名男生替代,那么至少有多少种选法?
(3)如果三个组的志愿者都不能重复,且性别不全相同,那么共有多少种选法?(不计算出具体的数字,列出式子即可)
您最近一年使用:0次
名校
2 . 为了迎接到校访问的同学,需要分上午、下午和晚上三个组各安排5名本校学生作为志愿者负责接待,并要求下午组的志愿者不能与上午组、晚上组的重复.某班共有40名学生,其中22名女生和18名男生,现准备从中选择志愿者.
(1)共有多少种选法?(可以不计算出具体的数字,列出式子即可)
(2)如果下午组中有一名男生请假,需要从班上的非志愿者中选一名男生替代,那么至少有多少种选法?
(3)如果三个组的志愿者都不能重复,且都要有男生和女生,那么共有多少种选法?
(1)共有多少种选法?(可以不计算出具体的数字,列出式子即可)
(2)如果下午组中有一名男生请假,需要从班上的非志愿者中选一名男生替代,那么至少有多少种选法?
(3)如果三个组的志愿者都不能重复,且都要有男生和女生,那么共有多少种选法?
您最近一年使用:0次
名校
解题方法
3 . 某单位在“全民健身日”举行了一场趣味运动会,其中一个项目为投篮游戏.游戏的规则如下:每局游戏需投篮3次,若投中的次数多于未投中的次数,该局得3分,否则得1分.已知甲投篮的命中率为 ,且每次投篮的结果相互独立.
,且每次投篮的结果相互独立.
(1)求甲在一局游戏中投篮命中次数X的分布列与期望;
(2)若参与者连续玩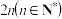 局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有
局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有 和
和 两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
 ,且每次投篮的结果相互独立.
,且每次投篮的结果相互独立.(1)求甲在一局游戏中投篮命中次数X的分布列与期望;
(2)若参与者连续玩
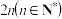 局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有
局投篮游戏获得的分数的平均值大于2,即可获得一份大奖.现有 和
和 两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
两种选择,要想获奖概率最大,甲应该如何选择?请说明理由.
您最近一年使用:0次
2021-08-07更新
|
1889次组卷
|
6卷引用:江苏省扬州市江都区丁沟中学2021-2022学年高二下学期期末模拟数学试题
名校
4 . 若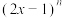 的展开式中第5项的二项式系数最大,则
的展开式中第5项的二项式系数最大,则
___________ .(写出一个即可)
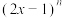 的展开式中第5项的二项式系数最大,则
的展开式中第5项的二项式系数最大,则
您最近一年使用:0次
2022-03-30更新
|
1507次组卷
|
6卷引用:河北省名校联盟2022届高三下学期联合调研数学试题
河北省名校联盟2022届高三下学期联合调研数学试题海南省普通高等学校招生2022届高三诊断性测试数学试题(已下线)押新高考第13题 二项式定理-备战2022年高考数学临考题号押题(新高考专用)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(6月1日)江苏省苏州大学附属中学2021-2022学年高二下学期期中数学试题浙江省绍兴市第一中学2022-2023学年高三上学期10月月考数学试题
解题方法
5 . 某电商为某次活动设计了“和谐”“爱国”“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包中的一种,若集齐三种红包即可获奖,且三种红包在4次点击中出现的顺序不同对应的奖次也不同,甲按规定依次点击了4次,直到第4次才获奖,求甲获得奖次的不同情形的种数.
您最近一年使用:0次
名校
解题方法
6 . 理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
您最近一年使用:0次
2017-07-23更新
|
322次组卷
|
2卷引用:新疆维吾尔自治区喀什第六中学2023届高三上学期期中数学(理)试题
2019·安徽蚌埠·一模
名校
7 . 某电商为某次活动设计了“和谐”、“爱国”、“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同 员工甲按规定依次点击了4次,直到第4次才获奖
员工甲按规定依次点击了4次,直到第4次才获奖 则他获得奖次的不同情形种数为
则他获得奖次的不同情形种数为

 员工甲按规定依次点击了4次,直到第4次才获奖
员工甲按规定依次点击了4次,直到第4次才获奖 则他获得奖次的不同情形种数为
则他获得奖次的不同情形种数为

| A.9 | B.12 | C.18 | D.24 |
您最近一年使用:0次
2019-04-12更新
|
1374次组卷
|
9卷引用:6.1分类加法计数原理与分步乘法计数原理 C卷
(已下线)6.1分类加法计数原理与分步乘法计数原理 C卷【市级联考】安徽省蚌埠市2019届高三第一次教学质量检查考试数学(理)试题河南省周口市西华县2018-2019学年高二下学期期中考试数学(理)试题江苏省南通市海安高级中学2019-2020学年高二下学期期中数学试题人教B版(2019) 选择性必修第二册 过关斩将 第三章 排列、组合与二项式定理 3.1 排列与组合 3.1.1基本计数原理(已下线)3.1.1 基本计数原理 B提高练(已下线)【新教材精创】6.1分类加法计数原理与分步乘法计数原理(1) -A基础练人教A版(2019) 选修第三册 突围者 第六章 第一节 分类加法计数原理与分布乘法计数原理(已下线)6.1 分类加法计数原理与分步乘法计数原理(第1课时)(分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)
8 . 十八世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸连接起来.有人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完这七座桥,最后回到出发点,这就是著名的哥尼斯堡七桥问题(下简称七桥问题),很多人尝试解决这个问题,但绞尽脑汁,就是无法找到答案.直到1736年,29岁的欧拉以拉丁文正式发表了论文《关于位置几何问题的解决》,文中详细讨论了七桥问题并作了一些推广.该论文被认为是图论、拓扑学和网络科学的发端.图1是欧拉当年解决七桥问题的手绘图,图2是该问题相应的示意图,其中A,B,C,D四个点代表陆地,连接这些点的边就是桥.欧拉将七桥问题转化成一个几何问题——一笔画问题.一笔画问题中,要求不遗漏地依次走完每一条边,允许重复走过某些结点,可以不回到出发点,但不允许重复走过任何一条边.___________ ,不同的走法总数为___________ .
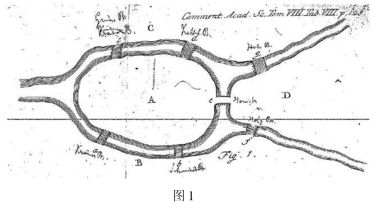
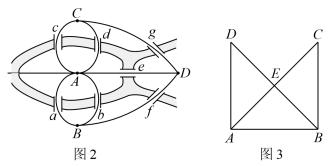
您最近一年使用:0次
2020高三·全国·专题练习
名校
解题方法
9 .  年春节联欢晚会以“共圆小康梦、欢乐过大年”为主题,突出时代性、人民性、创新性,节目内容丰富多彩,呈现形式新颖多样.某小区的
年春节联欢晚会以“共圆小康梦、欢乐过大年”为主题,突出时代性、人民性、创新性,节目内容丰富多彩,呈现形式新颖多样.某小区的 个家庭买了
个家庭买了 张连号的门票,其中甲家庭需要
张连号的门票,其中甲家庭需要 张连号的门票,乙家庭需要
张连号的门票,乙家庭需要 张连号的门票,剩余的
张连号的门票,剩余的 张随机分到剩余的
张随机分到剩余的 个家庭即可,则这
个家庭即可,则这 张门票不同的分配方法的种数为( )
张门票不同的分配方法的种数为( )
 年春节联欢晚会以“共圆小康梦、欢乐过大年”为主题,突出时代性、人民性、创新性,节目内容丰富多彩,呈现形式新颖多样.某小区的
年春节联欢晚会以“共圆小康梦、欢乐过大年”为主题,突出时代性、人民性、创新性,节目内容丰富多彩,呈现形式新颖多样.某小区的 个家庭买了
个家庭买了 张连号的门票,其中甲家庭需要
张连号的门票,其中甲家庭需要 张连号的门票,乙家庭需要
张连号的门票,乙家庭需要 张连号的门票,剩余的
张连号的门票,剩余的 张随机分到剩余的
张随机分到剩余的 个家庭即可,则这
个家庭即可,则这 张门票不同的分配方法的种数为( )
张门票不同的分配方法的种数为( )A.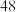 |
B. |
C.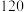 |
D.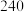 |
您最近一年使用:0次
2021-01-16更新
|
2233次组卷
|
11卷引用:第十二章 统计与概率专练2—排列组合2-2022届高三数学一轮复习
(已下线)第十二章 统计与概率专练2—排列组合2-2022届高三数学一轮复习重庆市第八中学校2021-2022学年高二下学期6月月考数学试题(已下线)专题61 统计与概率综合练习-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题61 统计与概率综合练习-2021年高考一轮数学(理)单元复习一遍过北京市日坛中学2020-2021学年高二下学期期中考试数学试题山东省(新高考)2021届高三模拟冲关押题卷(二)数学试题人教B版(2019) 选修第二册 名师精选 第三章 排列、组合与二项式定理苏教版(2019) 选修第二册 名师精选 第七章 计数原理山西省太原市2023届高三上学期1月第一次联考数学试题湖南省娄底市部分学校2023届高三三模数学试题山西省山西大学附属中学校2023届高三下学期5月月考数学试题
10 . 从由1,2,3,4,5,6组成的没有重复数字的六位数中任取5个不同的数,其中满足1,3都不与5相邻的六位偶数的个数为随机变量X,则P(X=2)=_____ .(结果用式子表示即可)
您最近一年使用:0次
2019-01-22更新
|
2290次组卷
|
6卷引用:专题7综合闯关(提升版)
(已下线)专题7综合闯关(提升版)2018-2019学年北师大版高中数学选修2-3同步配套(课件+练习):2.2人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 专题强化练4 二项分布与超几何分布沪教版(2020) 选修第二册 堂堂清 第7章 7.3(2)常用分布(超几何分布)(已下线)7.4.2 超几何分布 (精练)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练



