名校
解题方法
1 . 已知函数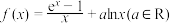 .
.
(1)当 时,证明:
时,证明: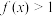 ;
;
(2)若 在区间
在区间 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数 的取值范围.
的取值范围.
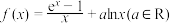 .
.(1)当
 时,证明:
时,证明: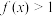 ;
;(2)若
 在区间
在区间 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-03更新
|
1378次组卷
|
3卷引用:江西省部分学校2024届高三下学期5月月考数学试题
名校
解题方法
2 . 给出以下三个材料:
①若函数 的导数为
的导数为 ,
, 的导数叫做
的导数叫做 的二阶导数,记作
的二阶导数,记作 .类似地,二阶导数
.类似地,二阶导数 的导数叫做
的导数叫做 的三阶导数,记作
的三阶导数,记作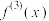 ,三阶导数
,三阶导数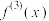 的导数叫做
的导数叫做 的四阶导数…,一般地,n-1阶导数的导数叫做
的四阶导数…,一般地,n-1阶导数的导数叫做 的n阶导数,即
的n阶导数,即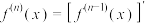 ,
, ;
;
②若 ,定义
,定义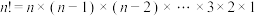 ;③若函数
;③若函数 在包含
在包含 的某个开区间
的某个开区间 上具有n阶的导数,那么对于
上具有n阶的导数,那么对于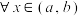 有
有 ,我们将
,我们将 称为函数
称为函数 在点
在点 处的n阶泰勒展开式.例如,
处的n阶泰勒展开式.例如, 在点
在点 处的n阶泰勒展开式为
处的n阶泰勒展开式为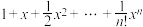 .根据以上三段材料,完成下面的题目:
.根据以上三段材料,完成下面的题目:
(1)若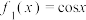 ,
, 在点
在点 处的3阶泰勒展开式分别为
处的3阶泰勒展开式分别为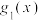 ,
,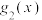 ,求出
,求出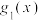 ,
,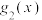 ;
;
(2)比较(1)中 与
与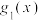 的大小;
的大小;
(3)证明: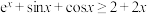 .
.
①若函数
 的导数为
的导数为 ,
, 的导数叫做
的导数叫做 的二阶导数,记作
的二阶导数,记作 .类似地,二阶导数
.类似地,二阶导数 的导数叫做
的导数叫做 的三阶导数,记作
的三阶导数,记作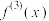 ,三阶导数
,三阶导数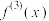 的导数叫做
的导数叫做 的四阶导数…,一般地,n-1阶导数的导数叫做
的四阶导数…,一般地,n-1阶导数的导数叫做 的n阶导数,即
的n阶导数,即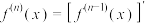 ,
, ;
;②若
 ,定义
,定义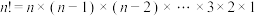 ;③若函数
;③若函数 在包含
在包含 的某个开区间
的某个开区间 上具有n阶的导数,那么对于
上具有n阶的导数,那么对于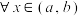 有
有 ,我们将
,我们将 称为函数
称为函数 在点
在点 处的n阶泰勒展开式.例如,
处的n阶泰勒展开式.例如, 在点
在点 处的n阶泰勒展开式为
处的n阶泰勒展开式为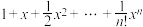 .根据以上三段材料,完成下面的题目:
.根据以上三段材料,完成下面的题目:(1)若
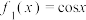 ,
, 在点
在点 处的3阶泰勒展开式分别为
处的3阶泰勒展开式分别为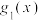 ,
,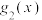 ,求出
,求出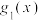 ,
,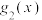 ;
;(2)比较(1)中
 与
与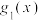 的大小;
的大小;(3)证明:
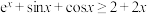 .
.
您最近一年使用:0次
2024·全国·模拟预测
名校
3 . 已知函数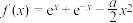 有三个极值点
有三个极值点 .
.
(1)求实数 的取值范围;
的取值范围;
(2)求证: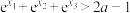 .
.
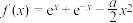 有三个极值点
有三个极值点 .
.(1)求实数
 的取值范围;
的取值范围;(2)求证:
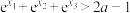 .
.
您最近一年使用:0次
4 . 已知函数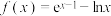 .
.
(1)求 的单调区间,
的单调区间,
(2)已如 .若函数
.若函数 有唯一的零点
有唯一的零点 .证明,
.证明,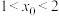 .
.
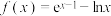 .
.(1)求
 的单调区间,
的单调区间,(2)已如
 .若函数
.若函数 有唯一的零点
有唯一的零点 .证明,
.证明,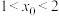 .
.
您最近一年使用:0次
2024·全国·模拟预测
名校
解题方法
5 . 已知实数 ,
,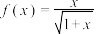 ,
,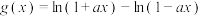 .
.
(1)求 的值;
的值;
(2)若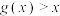 对
对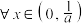 恒成立,求a的最小值;
恒成立,求a的最小值;
(3)当正整数 时,求证:
时,求证: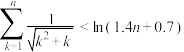 .
.
 ,
,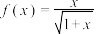 ,
,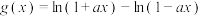 .
.(1)求
 的值;
的值;(2)若
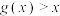 对
对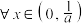 恒成立,求a的最小值;
恒成立,求a的最小值;(3)当正整数
 时,求证:
时,求证: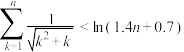 .
.
您最近一年使用:0次
2024-01-18更新
|
417次组卷
|
4卷引用:江西省上饶艺术学校2024届高三上学期1月月考数学试题
江西省上饶艺术学校2024届高三上学期1月月考数学试题(已下线)2024届数学新高考学科基地秘卷(六)广东省佛山市第一中学2024届高三上学期第二次调研数学试题(已下线)广东省佛山市第一中学2024届高三上学期第二次调研数学试题变式题17-22
6 . 已知函数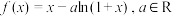 .
.
(1)讨论 的单调性;
的单调性;
(2)证明:对于任意正整数n,都有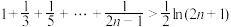 .
.
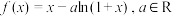 .
.(1)讨论
 的单调性;
的单调性;(2)证明:对于任意正整数n,都有
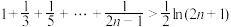 .
.
您最近一年使用:0次
2024-02-14更新
|
1216次组卷
|
6卷引用:江西省宜春市丰城市第九中学2023-2024学年高二下学期开学考试数学试题
江西省宜春市丰城市第九中学2023-2024学年高二下学期开学考试数学试题安徽省合肥市六校联盟2024届高三上学期期末数学试题(已下线)5.3.1函数的单调性 第三课 知识扩展延伸(已下线)重难点2-4 利用导数研究不等式与极值点偏移(8题型+满分技巧+限时检测)(已下线)第五章综合 第三练 方法提升应用(已下线)专题1 数列不等式 与导数结合 练(经典好题母题)
名校
解题方法
7 . 若函数 在
在 上有定义,且对于任意不同的
上有定义,且对于任意不同的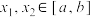 ,都有
,都有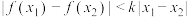 ,则称
,则称 为
为 上的“
上的“ 类函数”.
类函数”.
(1)若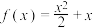 ,判断
,判断 是否为
是否为 上的“3类函数”;
上的“3类函数”;
(2)若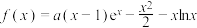 为
为 上的“2类函数”,求实数
上的“2类函数”,求实数 的取值范围;
的取值范围;
(3)若 为
为 上的“2类函数”,且
上的“2类函数”,且 ,证明:
,证明: ,
, ,
, .
.
 在
在 上有定义,且对于任意不同的
上有定义,且对于任意不同的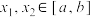 ,都有
,都有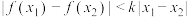 ,则称
,则称 为
为 上的“
上的“ 类函数”.
类函数”.(1)若
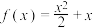 ,判断
,判断 是否为
是否为 上的“3类函数”;
上的“3类函数”;(2)若
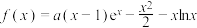 为
为 上的“2类函数”,求实数
上的“2类函数”,求实数 的取值范围;
的取值范围;(3)若
 为
为 上的“2类函数”,且
上的“2类函数”,且 ,证明:
,证明: ,
, ,
, .
.
您最近一年使用:0次
2024-01-25更新
|
2102次组卷
|
13卷引用:江西省2024届高三上学期一轮总复习验收考试数学试题
江西省2024届高三上学期一轮总复习验收考试数学试题江西省上饶市六校2024届高三第一次联合考试(2月)数学试卷广东省茂名市2024届高三一模数学试题广东省2024届高三上学期元月期末统一调研测试数学试卷安徽省阜阳市阜阳一中2023-2024学年高二下学期开学检测数学试题2024年新高考模拟卷数学试题(九省联考题型)(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)湖南省长沙市雅礼实验中学2023-2024学年高二下学期收心检测数学试题(已下线)2023-2024学年高二下学期第一次月考解答题压轴题十六大题型专练(1)河北省保定市唐县第一中学2023-2024学年高二下学期3月月考数学试题河北省石家庄一中2023-2024学年高二下学期第一次月考数学试题四川省仁寿实验中学2023-2024学年高二下学期4月期中考试数学试题吉林省长春市朝阳区长春吉大附中实验学校2023-2024学年高二下学期4月月考数学试题
8 . 设函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为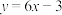 .
.
(1)求 ;
;
(2)证明: .
.
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为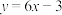 .
.(1)求
 ;
;(2)证明:
 .
.
您最近一年使用:0次
2024-01-21更新
|
2679次组卷
|
8卷引用:江西省抚州市临川第一中学2024届高三“九省联考”考后适应性测试数学试题(一)
江西省抚州市临川第一中学2024届高三“九省联考”考后适应性测试数学试题(一)陕西省榆林市2024届高三一模数学(文)试题(已下线)模块四 第五讲:利用导数证明不等式【练】陕西省汉中市2024届高三上学期第四次校际联考数学(文)试题(已下线)高三数学开学摸底考02(新考法,新高考七省地区专用)(已下线)最新模拟重组精华卷2 -模块一 各地期末考试精选汇编(已下线)重难点2-4 利用导数研究不等式与极值点偏移(8题型+满分技巧+限时检测)江苏省扬州市仪征中学2024届高三下学期期初调研测试数学试题
名校
解题方法
9 . 英国数学家泰勒发现了如下公式: 其中
其中 为自然对数的底数,
为自然对数的底数,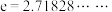 .以上公式称为泰勒公式.设
.以上公式称为泰勒公式.设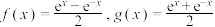 ,根据以上信息,并结合高中所学的数学知识,解决如下问题.
,根据以上信息,并结合高中所学的数学知识,解决如下问题.
(1)证明: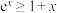 ;
;
(2)设 ,证明:
,证明: ;
;
(3)设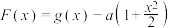 ,若
,若 是
是 的极小值点,求实数
的极小值点,求实数 的取值范围.
的取值范围.
 其中
其中 为自然对数的底数,
为自然对数的底数,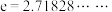 .以上公式称为泰勒公式.设
.以上公式称为泰勒公式.设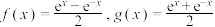 ,根据以上信息,并结合高中所学的数学知识,解决如下问题.
,根据以上信息,并结合高中所学的数学知识,解决如下问题.(1)证明:
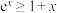 ;
;(2)设
 ,证明:
,证明: ;
;(3)设
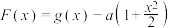 ,若
,若 是
是 的极小值点,求实数
的极小值点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-03-03更新
|
2275次组卷
|
18卷引用:江西省宜春市上高二中2024届高三下学期5月月考数学试卷
江西省宜春市上高二中2024届高三下学期5月月考数学试卷贵州省贵阳市2024届高三下学期适应性考试数学试卷(一)贵州省安顺市2024届高三下学期模拟考试(一)数学试卷云南省玉溪市第一中学2023-2024学年高二下学期3月月考数学试题海南省海南华侨中学2023-2024学年高三下学期第二次模拟考试数学试题重庆市礼嘉中学2023-2024学年高二下学期第一次月考数学试题吉林省通化市梅河口市第五中学2023-2024学年高二下学期第一次月考数学试题重庆第十一中学校2023-2024学年高二下学期3月月考数学试题重庆市璧山中学校2023-2024学年高二下学期第一次月考数学试题广东省东莞市光明中学2023-2024学年高二下学期第一次月考数学试题四川省达州外国语学校2023-2024学年高二下学期3月月考数学试题黑龙江省哈尔滨市双城区兆麟中学2023-2024学年高二下学期第一次月考(4月)数学试题重庆市荣昌中学校2023-2024学年高二下学期4月期中考试数学试题广东省广州市广州中学2023-2024学年高二下学期期中考试数学试题(已下线)专题11 利用泰勒展开式证明不等式【练】河北省石家庄四十一中2023-2024学年高二下学期第一次月考数学试题河北省石家庄二中润德中学2023-2024学年高二下学期第一次月考数学试题福建省宁德市古田县第一中学2024届高中毕业班高考前适应性测试数学试题
10 . 已知函数 .
.
(1)若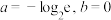 ,求
,求 的极值;
的极值;
(2)若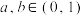 ,设
,设 .证明:
.证明:
(ⅰ)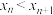 ;
;
(ⅱ)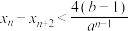 .
.
 .
.(1)若
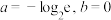 ,求
,求 的极值;
的极值;(2)若
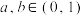 ,设
,设 .证明:
.证明:(ⅰ)
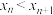 ;
;(ⅱ)
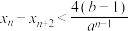 .
.
您最近一年使用:0次
2024-02-27更新
|
566次组卷
|
3卷引用:江西省名校教研联盟2024届高三下学期2月开学考试数学试卷



