解题方法
1 . 如图,正四棱锥 每一个侧面都是边长为4的正三角形,若点M在四边形ABCD内(包含边界)运动,N为PD的中点,则( )
每一个侧面都是边长为4的正三角形,若点M在四边形ABCD内(包含边界)运动,N为PD的中点,则( )
 每一个侧面都是边长为4的正三角形,若点M在四边形ABCD内(包含边界)运动,N为PD的中点,则( )
每一个侧面都是边长为4的正三角形,若点M在四边形ABCD内(包含边界)运动,N为PD的中点,则( )
A.当M为AD的中点时,异面直线MN与PC所成角为 |
B.当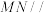 平面PBC时,点M的轨迹长度为 平面PBC时,点M的轨迹长度为 |
C.当 时,点M到AB的距离可能为 时,点M到AB的距离可能为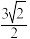 |
D.存在一个体积为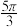 的圆柱体可整体放入正四棱锥 的圆柱体可整体放入正四棱锥 内 内 |
您最近半年使用:0次
名校
解题方法
2 . 易拉罐用料最省问题的研究.小明同学最近注意到一条新闻,易拉罐(如图所示)作为饮品的容器,每年的用量可达数万亿个.这让他想到一个用料最优化的问题,即在易拉罐的体积(容积)一定的情况下,如何确定易拉罐的高和半径才能使得用料最省?他研究发现易拉罐的上盖、下底和侧壁的厚度是不同的,进而结合数学建模知识进行了深入研究.以下是小明的研究过程,请回答其中问题.
(1)建立模型问题1: 填空:记圆柱容积为 ,高为
,高为 ,底面半径为
,底面半径为 , 则
, 则 ___________; ①记上盖、下底和侧壁的厚度分别为
___________; ①记上盖、下底和侧壁的厚度分别为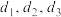 (底面半径都为
(底面半径都为 ),且侧壁展开可看成长方体(长、宽、高分别为
),且侧壁展开可看成长方体(长、宽、高分别为 ),金属用料总量为C(接口材料忽略不计),则
),金属用料总量为C(接口材料忽略不计),则 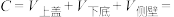 ___________ ;②因为
___________ ;②因为 都是常数,不妨设
都是常数,不妨设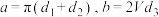 ,则由① ②可得用料总量的函数可简化为
,则由① ②可得用料总量的函数可简化为 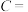 _____________(用
_____________(用 表示) ③;
表示) ③;
(2)求解模型:问题2:求解当 取何值时(用
取何值时(用 表示),
表示), 取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知
取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知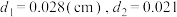
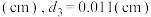 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得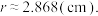 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
(3)模型评价与改进:问题3:模型计算结果与现实数据存在较大差异的原因可能为_________相应改进措施为__________.
注:只需一条原因及相应改进措施即可

(1)建立模型问题1: 填空:记圆柱容积为
 ,高为
,高为 ,底面半径为
,底面半径为 , 则
, 则 ___________; ①记上盖、下底和侧壁的厚度分别为
___________; ①记上盖、下底和侧壁的厚度分别为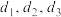 (底面半径都为
(底面半径都为 ),且侧壁展开可看成长方体(长、宽、高分别为
),且侧壁展开可看成长方体(长、宽、高分别为 ),金属用料总量为C(接口材料忽略不计),则
),金属用料总量为C(接口材料忽略不计),则 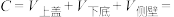 ___________ ;②因为
___________ ;②因为 都是常数,不妨设
都是常数,不妨设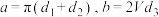 ,则由① ②可得用料总量的函数可简化为
,则由① ②可得用料总量的函数可简化为 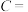 _____________(用
_____________(用 表示) ③;
表示) ③;(2)求解模型:问题2:求解当
 取何值时(用
取何值时(用 表示),
表示), 取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知
取得最小值,即用料最省?(写出解答过程)检验模型:小明上网查阅到目前330毫升可乐易拉罐的数据,得知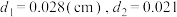
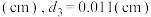 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得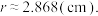 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优;(3)模型评价与改进:问题3:模型计算结果与现实数据存在较大差异的原因可能为_________相应改进措施为__________.
注:只需一条原因及相应改进措施即可
您最近半年使用:0次
名校
解题方法
3 . 某工件是底面半径为2,母线为4的圆锥,现将该工件通过切削,加工成一个长方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件体积的最大值为___________ .
您最近半年使用:0次
名校
解题方法
4 . 某口罩生产企业,在疫情期间每月生产 万件N95口罩的利润函数为
万件N95口罩的利润函数为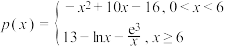 (单位:万元).
(单位:万元).
(1)当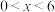 时,求企业平均每万件月利润的最大值.
时,求企业平均每万件月利润的最大值.
(2)当月产量为多少万件时,企业的月利润最大?请为企业生产经营提一些合理建议.
 万件N95口罩的利润函数为
万件N95口罩的利润函数为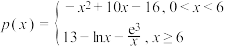 (单位:万元).
(单位:万元).(1)当
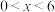 时,求企业平均每万件月利润的最大值.
时,求企业平均每万件月利润的最大值.(2)当月产量为多少万件时,企业的月利润最大?请为企业生产经营提一些合理建议.
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
5 . 圆O的半径为R,从中剪去一个扇形,剩余部分制成一个圆锥,则何时这个圆锥的体积最大?
您最近半年使用:0次
解题方法
6 . 将一条长为6的铁丝截成9段,拼成一个正三棱柱,求该三棱柱体积的最大值.
您最近半年使用:0次
2024·全国·模拟预测
7 . 已知球 的表面积为
的表面积为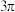 ,直四棱柱
,直四棱柱 的顶点均在球
的顶点均在球 的球面上,则该直四棱柱的体积的最大值为
的球面上,则该直四棱柱的体积的最大值为______ .
 的表面积为
的表面积为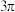 ,直四棱柱
,直四棱柱 的顶点均在球
的顶点均在球 的球面上,则该直四棱柱的体积的最大值为
的球面上,则该直四棱柱的体积的最大值为
您最近半年使用:0次
解题方法
8 . 某零食生产厂家准备用长为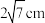 ,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盒容积的最大值为
,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盒容积的最大值为_________ 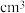 .
.
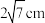 ,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盒容积的最大值为
,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盒容积的最大值为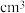 .
.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
9 . 已知球 的表面积为
的表面积为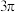 ,直四棱柱
,直四棱柱 的顶点均在球
的顶点均在球 的表面上,则直四棱柱
的表面上,则直四棱柱 的体积的最大值为
的体积的最大值为______ .
 的表面积为
的表面积为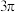 ,直四棱柱
,直四棱柱 的顶点均在球
的顶点均在球 的表面上,则直四棱柱
的表面上,则直四棱柱 的体积的最大值为
的体积的最大值为
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
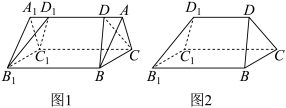
10 . 上海市政府实施“景观工程”,对现有平顶的民用多层住宅进行“平改坡”,计划将平顶房屋改为尖顶,并铺上彩色瓦片.现对某幢房屋有 两种改造方案:
两种改造方案: 方案中坡顶,如图1所示,为底面是等边三角形的直三棱柱,尖顶屋脊
方案中坡顶,如图1所示,为底面是等边三角形的直三棱柱,尖顶屋脊 与房屋长度
与房屋长度 等长,有两个坡面需铺上瓦片.
等长,有两个坡面需铺上瓦片. 方案中坡顶,如图2所示,为图削去两端相同的两个三棱锥而得,尖顶屋脊
方案中坡顶,如图2所示,为图削去两端相同的两个三棱锥而得,尖顶屋脊 比房屋长度
比房屋长度 短,有四个坡面需铺上瓦片.若房屋长
短,有四个坡面需铺上瓦片.若房屋长 ,宽
,宽 ,屋脊高为
,屋脊高为 ,要使铺设的瓦片比较省,请你选择
,要使铺设的瓦片比较省,请你选择 两种方案中的哪一个?
两种方案中的哪一个?
 两种改造方案:
两种改造方案: 方案中坡顶,如图1所示,为底面是等边三角形的直三棱柱,尖顶屋脊
方案中坡顶,如图1所示,为底面是等边三角形的直三棱柱,尖顶屋脊 与房屋长度
与房屋长度 等长,有两个坡面需铺上瓦片.
等长,有两个坡面需铺上瓦片. 方案中坡顶,如图2所示,为图削去两端相同的两个三棱锥而得,尖顶屋脊
方案中坡顶,如图2所示,为图削去两端相同的两个三棱锥而得,尖顶屋脊 比房屋长度
比房屋长度 短,有四个坡面需铺上瓦片.若房屋长
短,有四个坡面需铺上瓦片.若房屋长 ,宽
,宽 ,屋脊高为
,屋脊高为 ,要使铺设的瓦片比较省,请你选择
,要使铺设的瓦片比较省,请你选择 两种方案中的哪一个?
两种方案中的哪一个?
您最近半年使用:0次



