13-14高一下·湖北黄冈·期中
名校
解题方法
1 . 数列 的前
的前 项和
项和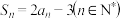 ,则数列
,则数列 的通项公式为
的通项公式为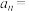
_______ .
 的前
的前 项和
项和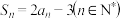 ,则数列
,则数列 的通项公式为
的通项公式为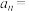
您最近一年使用:0次
13-14高三下·湖北黄冈·阶段练习
2 . 设数列 的前
的前 项和为
项和为 ,已知
,已知 ,
,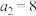 ,
, ,
, 是数列
是数列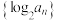 的前
的前 项和.
项和.
(1)求数列 的通项公式;(2)求
的通项公式;(2)求 ;
;
(3)求满足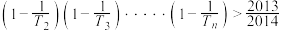 的最大正整数
的最大正整数 的值.
的值.
 的前
的前 项和为
项和为 ,已知
,已知 ,
,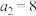 ,
, ,
, 是数列
是数列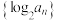 的前
的前 项和.
项和.(1)求数列
 的通项公式;(2)求
的通项公式;(2)求 ;
;(3)求满足
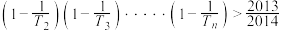 的最大正整数
的最大正整数 的值.
的值.
您最近一年使用:0次
13-14高三下·湖北黄冈·阶段练习
解题方法
3 . 已知等比数列 的各项均为正数,且
的各项均为正数,且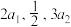 成等差数列,
成等差数列, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)已知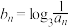 ,记
,记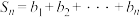 ,
,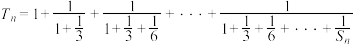 ,求证:
,求证: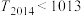 .
.
 的各项均为正数,且
的各项均为正数,且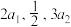 成等差数列,
成等差数列, 成等比数列.
成等比数列.(1)求数列
 的通项公式;
的通项公式;(2)已知
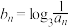 ,记
,记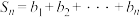 ,
,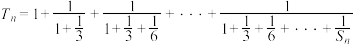 ,求证:
,求证: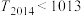 .
.
您最近一年使用:0次
2014·浙江嘉兴·一模
4 . 已知实数等比数列 的前n项和为
的前n项和为 ,则下列结论一定成立的是
,则下列结论一定成立的是
 的前n项和为
的前n项和为 ,则下列结论一定成立的是
,则下列结论一定成立的是A.若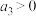 ,则 ,则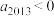 | B.若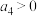 ,则 ,则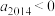 |
C.若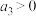 ,则 ,则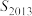 >0 >0 | D.若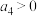 ,则 ,则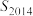 >0 >0 |
您最近一年使用:0次
2016-12-02更新
|
1386次组卷
|
4卷引用:2015届湖北省黄冈中学等八校高三12月第一次联考文科数学试卷
2015届湖北省黄冈中学等八校高三12月第一次联考文科数学试卷(已下线)2014届浙江嘉兴市高三3月教学测试(一)(即一模)理科数学试卷2018届高三数学训练题(40):数列中的易错题 陕西省西安市第二中学2023-2024学年高三上学期第四次考试数学试题
13-14高三·湖北黄冈·期末
5 . 等比数列 的前n项和
的前n项和 ,已知
,已知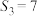 ,且
,且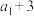 ,
, ,
,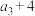 成等差数列.
成等差数列.
(1)求数列 的公比q和通项
的公比q和通项 ;
;
(2)若 是递增数列,令
是递增数列,令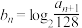 ,求
,求 .
.
 的前n项和
的前n项和 ,已知
,已知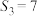 ,且
,且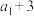 ,
, ,
,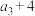 成等差数列.
成等差数列. (1)求数列
 的公比q和通项
的公比q和通项 ;
; (2)若
 是递增数列,令
是递增数列,令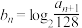 ,求
,求 .
.
您最近一年使用:0次
2016-12-02更新
|
681次组卷
|
4卷引用:2014届湖北黄冈市高三年级秋季期末考试理科数学试卷
(已下线)2014届湖北黄冈市高三年级秋季期末考试理科数学试卷2014-2015学年安徽省皖中“四校联盟”高一下学期联考理科数学试卷2014-2015学年安徽省皖中“四校联盟”高一下学期联考文科数学试卷2016-2017学年福建南安侨光中学高二理上第一次阶段考试数学试卷
2013·北京顺义·二模
6 . 已知数列 中,
中, ,等比数列
,等比数列 的公比
的公比 满足
满足 且
且 ,则
,则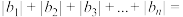 ( )
( )
 中,
中, ,等比数列
,等比数列 的公比
的公比 满足
满足 且
且 ,则
,则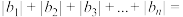 ( )
( )A. | B.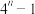 |
C. | D. |
您最近一年使用:0次
2016-12-04更新
|
639次组卷
|
6卷引用:2017届湖北黄冈中学高三上学期周末测试9.10数学试卷
12-13高三上·湖北黄冈·期末
7 . 已知数列 中,
中, ,前n项和为
,前n项和为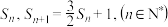
(1)求数列 的通项公式;
的通项公式;
(2)设数列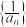 的前n项和为
的前n项和为 ,求满足不等式
,求满足不等式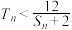 的n值.
的n值.
 中,
中, ,前n项和为
,前n项和为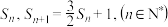
(1)求数列
 的通项公式;
的通项公式;(2)设数列
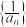 的前n项和为
的前n项和为 ,求满足不等式
,求满足不等式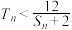 的n值.
的n值.
您最近一年使用:0次
8 . 已知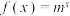 (
( 为常数,
为常数, 且
且 ).设
).设 、
、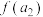 、
、 、
、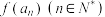 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(1)求证:数列 是等差数列;
是等差数列;
(2)若 ,且数列
,且数列 的前
的前 项和为
项和为 ,当
,当 时,求
时,求 ;
;
(3)若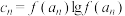 ,问是否存在
,问是否存在 ,使得数列
,使得数列 中每一项恒小于它后面的项?若存在,求出
中每一项恒小于它后面的项?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
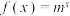 (
( 为常数,
为常数, 且
且 ).设
).设 、
、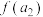 、
、 、
、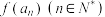 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.(1)求证:数列
 是等差数列;
是等差数列;(2)若
 ,且数列
,且数列 的前
的前 项和为
项和为 ,当
,当 时,求
时,求 ;
;(3)若
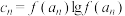 ,问是否存在
,问是否存在 ,使得数列
,使得数列 中每一项恒小于它后面的项?若存在,求出
中每一项恒小于它后面的项?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
9 . 已知数列 中,
中, ,
,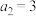 ,其前
,其前 项和为
项和为 ,且当
,且当 时,
时, .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)令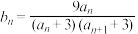 ,记数列
,记数列 的前
的前 项和为
项和为 ,证明对于任意的正整数
,证明对于任意的正整数 ,都有
,都有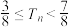 成立.
成立.
 中,
中, ,
,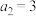 ,其前
,其前 项和为
项和为 ,且当
,且当 时,
时, .
.(Ⅰ)求证:数列
 是等比数列;
是等比数列;(Ⅱ)求数列
 的通项公式;
的通项公式;(Ⅲ)令
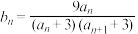 ,记数列
,记数列 的前
的前 项和为
项和为 ,证明对于任意的正整数
,证明对于任意的正整数 ,都有
,都有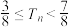 成立.
成立.
您最近一年使用:0次

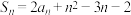 ,
, ,
,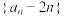 为等比数列;
为等比数列;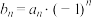 ,求数列
,求数列 ;
; ,数列
,数列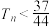 .
.


